关于半波长输电的几个原理性问题
2018-12-12徐政,杨健
徐 政, 杨 健
(浙江大学电气工程学院, 浙江 杭州 310027)
0 引言
在巴西、俄罗斯、中国等国家,能源基地可能远离主要负荷中心[1-3],半波长距离输电在这种情况下是一种很有吸引力的选项。十九世纪四十年代,人们就对这种输电技术进行了研究,但至今,世界上还没有实际投入运行的半波长输电系统[4-5]。半波长输电的可行性仍需要进一步研究。
现有研究对半波长输电的基本特性进行了分析,已有文献宣称半波长输电系统具有如下优点:(1) 半波长输电线路不存在一般远距离输电线路运行时可能出现的费兰梯效应、充电电流过大、发电机自激等问题[6];(2) 半波长输电线路不需要补偿装置和开关站[7-8];(3) 半波长输电线路可以认为与短线路等效,同步稳定性不是制约输送功率的主要因素[6];(4) 半波长输电技术具有一定的经济性。文献[9—11]论证了半波长输电技术与高压直流输电技术相比,具有经济上的优势。
然而,上述半波长输电系统的优点还没有完全在理论上得到支撑。同时,半波长输电技术仍存在一些技术上的问题,其中,过电压和同步稳定性是可行性分析中最重要的两个技术问题。已有研究发现,对半波长输电系统,其稳态过电压水平与系统传输的功率和功率因数有关[12]。为了避免稳态过电压,输电功率不应大于自然功率(surge imped-ance loading, SIL)[13-15]。小干扰稳定方面,等效电气距离稍大于半波长的系统被认为是可行的[6,12,16],但还没有文献明确给出等效电气距离的可行范围。实际上,可行范围与系统的谐振输电距离有关,这一点将在本文中进行具体说明。
在三相短路和不对称故障下,系统无法避免产生严重的工频过电压[17]。同时,系统的暂态稳定性与故障类型和故障位置有关[12,18-19]。对于三相短路故障,已有文献给出了系统最大过电压的理论解释[12,20],但对于暂态稳定性,大多数研究都是通过仿真进行说明,缺乏理论支撑。
本文在考虑过电压和稳定性的条件下,寻找半波长输电系统的可行输电距离。在这个过程中,提出了谐振输电距离和同步系数的概念,以反映系统稳态和小干扰稳定特性,定义并推导了最严重故障点,以研究三相短路故障下的系统暂态特性。
1 电路模型
远距离交流输电系统主要应用于点对网或者网对网输电系统。对于这两种情况,其稳态特性和同步稳定性分析都可以采用单机对无穷大系统模型。因此,考虑送端系统和受端系统作用后,一般性的远距离交流输电系统可以用图1所示的电路模型来表示。其中,输电线路采用正序分布参数模型,送端机组采用“次暂态电抗后电势恒定”模型,受端交流系统采用正序戴维南等值电路。

图1 远距离交流输电系统电路模型Fig.1 Equivalent circuit of the long distance transmission system
如图1所示,Eg为送端机组等值电势;Xg为送端机组等值电抗;Er,Xr分别为受端系统等值电势和等值电抗;Us,Ur分别为输电线路送、受端电压;Is,Ir分别为送、受端电流;Ux是距离输电线路送端xkm处的电压;l是输电线路长度(或称为输电距离);Pg,Qg分别为送端有功和无功功率;Pr,Qr分别为受端有功和无功功率。
远距离输电线路的基本特性可用长线方程描述:
Ur=Uschγl-IsZCshγl
(1)
Ir=-Usshγl/ZC+Ischγl
(2)
其中,γ为传播系数;ZC为波阻抗。两者可分别通过下式计算:
(3)
(4)
式中:L1,C1,G1,R1分别为输电线路单位长度的正序电感、电容、电导和电阻;ω为系统角频率;α为衰减系数,β为相位系数。
为描述系统特性和数值计算方便,本文针对测试系统进行分析。测试系统基准频率为50 Hz。采用文献[21—22]中的线路参数,如表1所示。
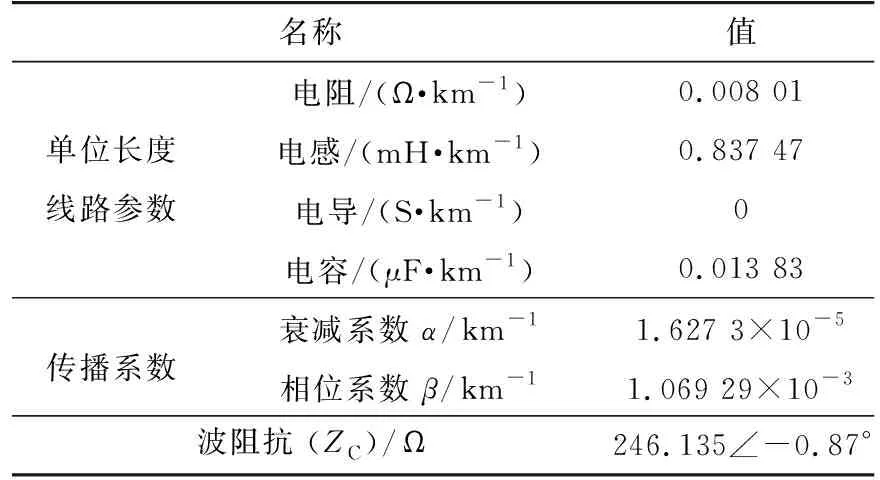
表1 输电线路参数Tab.1 Transmission Line parameters
由表1可见,衰减系数α远小于相位系数β;同时,波阻抗ZC的相角约等于0。这些参数与线路无损时的情况很相似。
测试系统半波长(l/2)为:
λ/2=π/β=2 938.0 km
(5)
当线路额定电压(Urated)取1000 kV时,线路的自然功率为:
(6)
本文分析中,选取Urated和PSIL作为电压基值和功率基值。采用大写字母表示物理量的实际值,小写字母表示物理量的标幺值。
为对能源基地通过半波长输电线路向负荷中心输电的典型应用场景进行分析,假设测试系统的送受端参数如表2所示。

表2 送受端系统参数Tab.2 Parameters of the sending-end and the receiving-end systems
在忽略线路损耗的情况下,根据图1和长线方程,可以求得:
(7)
若用角度θ表示相位系数β与输电距离l的乘积,即θ=βl,则式(7)中导纳矩阵y可表示为::
(8)
Δ0=(1-xgxr)sinθ+(xg+xr)cosθ
(9)
根据式(7),可以计算得到标幺值下的功率方程为:
(10)
(11)
(12)
其中,eg,er分别为设定的送、受端边界条件;δg是eg和er之间的相角差。
类似地,可以得到考虑线路损耗情况下的功率方程如下:
(13)
(14)
(15)
(16)
(17)
Δloss=|(xgxr-zc2)shγl-jzc(xg+xr)chγl|2
(18)
其中,在输电线路参数及xg,xr,eg,er确定的条件下,C1~C6,φ1~φ4均为常数,其具体表达式参见附录A。
2 谐振输电距离
根据式(9)可知:

(19)
其中:
(20)
当θ=π-φC,即l=(π-φC)/β时,Δ0= 0。根据式(8)可知,此时导纳矩阵y中各元素分母为0,输电线路与两侧系统等值电抗之间发生串联谐振。定义此时的输电距离为谐振输电距离,并用lresnt表示,则:
(21)
由式(21)可见,lresnt只与输电线路参数和两侧系统等值电抗有关,而与eg,er无关。
对于考虑线路损耗的情况,由式(18)可知,系统的谐振输电距离lresnt仍可用式(21)进行计算。对于本文中的测试系统,lresnt约为2707 km,βlresnt约为165.8°。
为分析输电距离在lresnt附近时的系统特性,设定系统具有一般性的边界条件:eg= 1.1 p.u.,er= 1.0 p.u.,则此时可以计算得到不同pg下的发电机无功功率qg随l的变化情况,结果如图2所示。

图2 不同输送距离和输送功率下的qgFig. 2 qg of different transmission power and transmission distances
如图2所示,线路长度l在lresnt附近(2700~2715 km)时,由于式(13)无解,系统无法运行。当线路长度l刚超出上述范围时,系统可以运行,但发电机无功功率的绝对值很大。如:当θ=βl= 167°(即l约为2726 km)且pg分别为0 p.u.,0.5 p.u.,1.0 p.u.和1.5 p.u.时,qg分别为5.81 p.u.,4.06 p.u.,2.69 p.u.和1.53 p.u.。可见,pg越小,qg的绝对值越大。
随着l与lresnt间距离的增大,发电机无功功率qg的绝对值逐渐减小。当l小于2639 km或大于2804 km时,不同pg下的发电机无功功率绝对值均减小到1 p.u.以下。
因此,为使系统可以运行,并使发电机无功功率处于合理范围内,输电距离需要远离lresnt。
3 稳态过电压分析
为进一步确定可行的输电距离范围,首先对系统稳态下的过电压特性进行分析。根据长线方程可得,距离线路送端xkm处的电压为:
ux=uschγx-iszCshγx
(22)
其中:
is=[(pg+jqg)/eg]*
(23)
us=eg-jisxg
(24)
其中,*表示取复数的共轭。
对于不同的输送距离l,整条线路中出现的最大电压分别记为ul,max。在设定的送、受端边界条件eg= 1.1 p.u.,er= 1.0 p.u.下,对于不同pg和不同的输送距离,可以根据式(22)计算得到沿线电压值,并进一步得到ul,max。ul,max结果如图3所示,其中图3(a)为输送距离在大范围内变化时的结果,图3(b)为小范围内的结果。
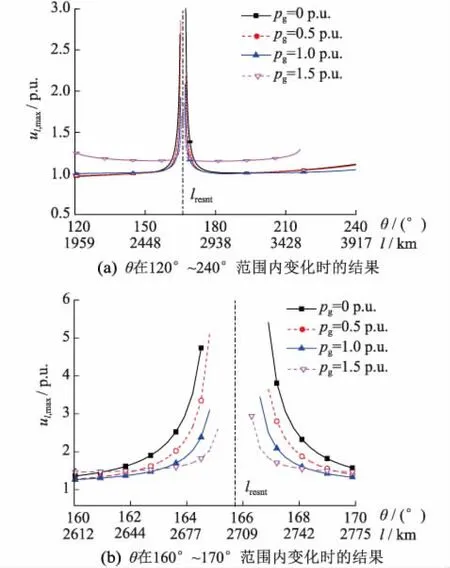
图3 不同输送距离下的最大过电压值Fig. 3 Maximum voltage along the line for different transmission distances
由图3可知:(1) 对于不同的pg,当l接近lresnt时,ul,max均明显增大;(2) 如图3(b)所示,当θ在163.3°~164.6°或167°~168.2°之间时,ul,max随pg的增大而减小;(3) 如图3(a)所示,当pg为1.5 p.u.时,θ在120°~240°范围内变化时,线路中总会出现明显的过电压,且大多数情况下,ul,max在数值上与pg相近。实际上,对pg大于1.0 p.u.情况,上述结论均成立;(4) 如图3(a)所示,当pg为1.5 p.u.且θ大于217.1°时,系统无运行点;类似地,由图3(b)可知,当pg为0 p.u.且θ在164.6°~167.0°之间时,系统也无运行点。
图3只给出了沿线最大过电压(ul,max)的值,还需要知道最大过电压出现的位置。我们将沿线最大过电压(ul,max)出现的位置记为xumax(以km为单位)或ul,max(以度为单位)或φumax(φumax=βxumax,以弧度或度为单位)。不同输电距离下,最大过电压及其出现的位置如图4所示,具体数值在表3中给出。
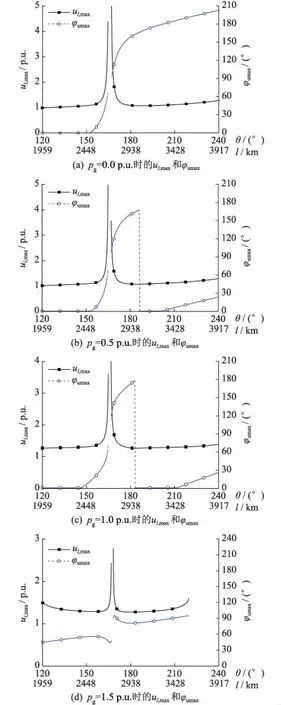
图4 不同输送距离和输送功率下的 最大过电压及其出现位置Fig.4 Maximum voltage along the line and the location where it appears.
表3 图4中特定点的具体数值Tab.3 Description of specified points in Fig.4
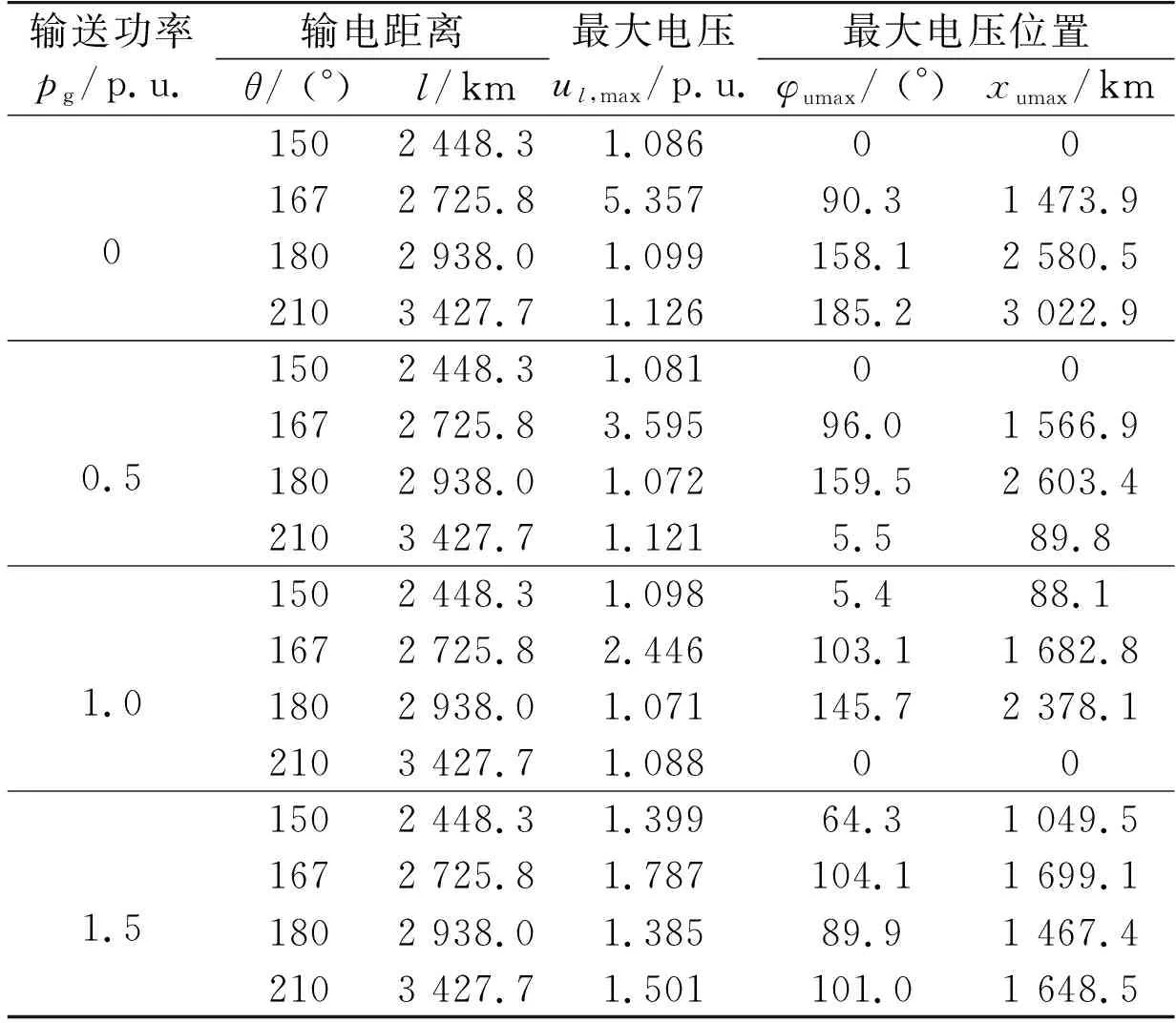
输送功率pg/p.u.输电距离θ/ (°)l/km最大电压ul,max/p.u.最大电压位置φumax/ (°)xumax/km1502 448.31.0860001672 725.85.35790.31 473.91802 938.01.099158.12 580.52103 427.71.126185.23 022.91502 448.31.081000.51672 725.83.59596.01 566.91802 938.01.072159.52 603.42103 427.71.1215.589.81502 448.31.0985.488.11.01672 725.82.446103.11 682.81802 938.01.071145.72 378.12103 427.71.088001502 448.31.39964.31 049.51.51672 725.81.787104.11 699.11802 938.01.38589.91 467.42103 427.71.501101.01 648.5
如图4和表3所示,以pg= 1.0 p.u.为例,当输电距离为2 448.3 km(150°),2 725.8 km(167°),2 938.0 km(180°)和3 427.7 km(210°)时,整条线路中最大过电压分别为1.098 p.u.,2.446 p.u., 1.071 p.u.和1.088 p.u.,最大过电压出现的位置分别为88.1 km (5.4°),1 682.8 km (103.1°),2 378.1 km (145.7°)和0.0 km (0°)。
如果选择ul,max<1.5 p.u.作为可接受的电压范围,则当pg在0~1.5 p.u.范围内变化时,测试系统的可行输电距离范围为:
(25)
4 小干扰稳定性分析
发电机的转子运动方程为:
(26)
式中:ω0,ωg,H,pm,D分别为系统额定角频率、发电机实际角频率、发电机惯性时间常数、发电机机械功率和发电机阻尼系数。在机械功率pm保持不变的假设条件下,可得到转子运动方程在工作点(δg(0),ω0)处的线性化方程为:
(27)
由式(27)可知,上述单机对无穷大系统的特征方程为:
(28)
由于H和D都是正数,因此系统小干扰稳定的条件最终变为:
(29)
定义Ksynch为同步系数,则半波长输电系统的小干扰稳定特性可以总结为:如果Ksynch为正,则系统小干扰稳定;如果Ksynch为负,则系统小干扰不稳定。
在设定的送、受端边界条件eg=1.1 p.u.,er=1.0 p.u.下,可以得到测试系统在不同输送功率下,Ksynch随输电距离l的变化情况。结果见图5和表4。

图5 不同功率水平下Ksynch随l变化的曲线Fig.5 Ksynch of different transmission power and transmission distances
表4 图5中特定点的具体数值Tab.4 Description of specified points in Fig.5
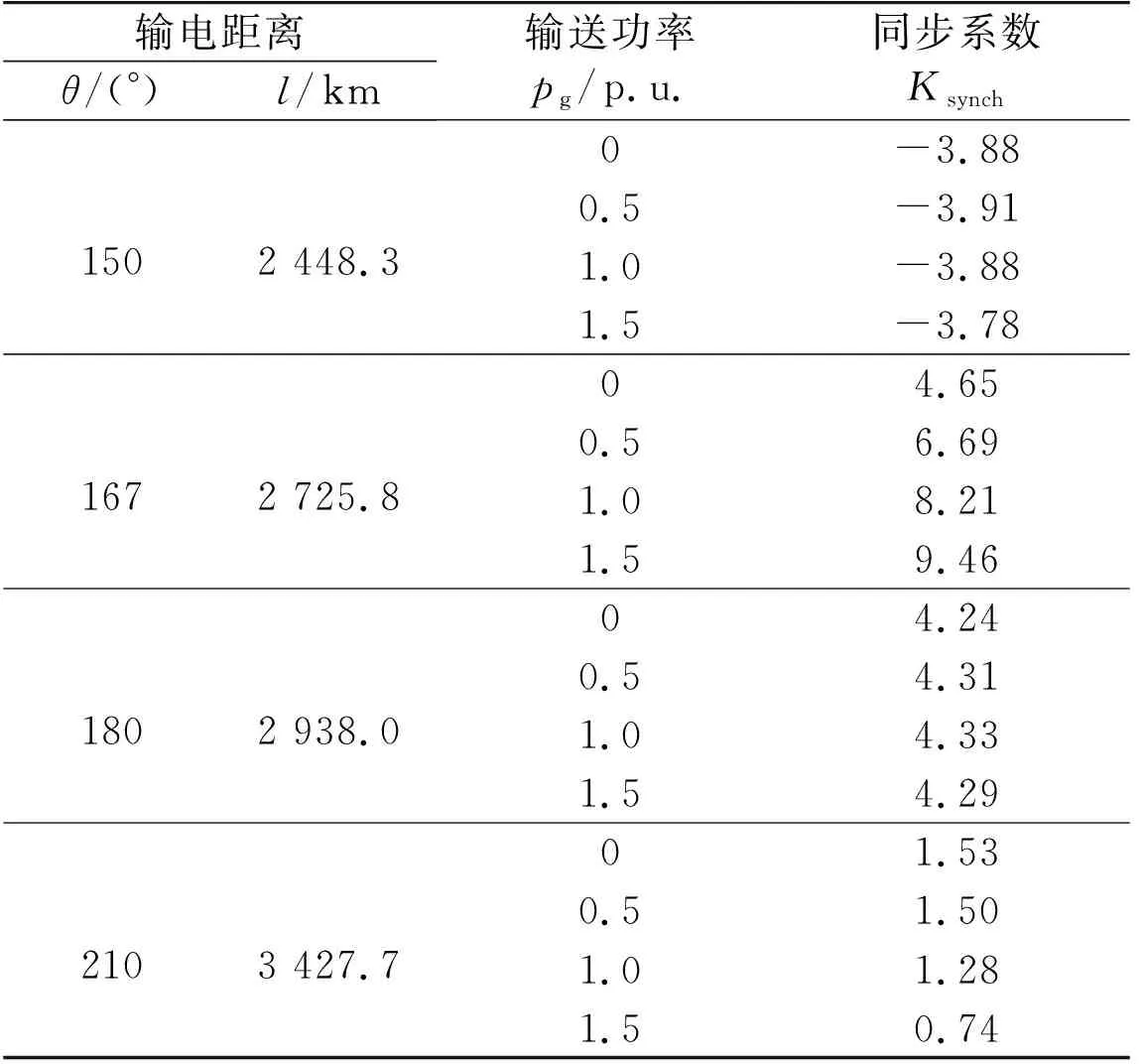
输电距离θ/(°)l/km输送功率pg/p.u.同步系数Ksynch0-3.881502 448.30.5-3.911.0-3.881.5-3.7804.651672 725.80.56.691.08.211.59.4604.241802 938.00.54.311.04.331.54.2901.532103 427.70.51.501.01.281.50.74
如图5和表4所示,以θ= 150°为例,当pg分别为0 p.u.,0.5 p.u.,1.0 p.u和1.5 p.u.时,Ksynch分别为-3.88,-3.91,-3.88 和 -3.78。由图5可知,在所研究的输电距离范围内,当l小于lresnt时,Ksynch为负;当l大于lresnt时(如θ= 167°),Ksynch为正。因此,只有在l大于lresnt时,系统小干扰下才可能稳定。
当考虑输送功率在0到1.5 p.u.范围内变化时,测试系统能保持小干扰同步稳定性的输电距离范围为:
166.8°<θ<217.1°
(30)
5 可行输电距离分析
综合考虑过电压约束给出的可行输电距离范围式(25)和小干扰同步稳定性约束给出的输电距离范围式(30),当输送功率在0到1.5 p.u.变化时,测试系统的可行输电距离范围为:
170.1°<θ<210.0°
(31)
综合考虑到电力系统在暂态过程中的频率变化,这里设定的允许的频率变化范围为额定频率的±3%,可以得到θ随频率偏差的变化曲线,如图6所示。

图6 θ随频率偏差的变化曲线Fig.6 θof different frequency
由图6可以看出,当频率偏差取-3%时,能同时满足过电压约束和同步稳定性约束的可行输电距离范围为:
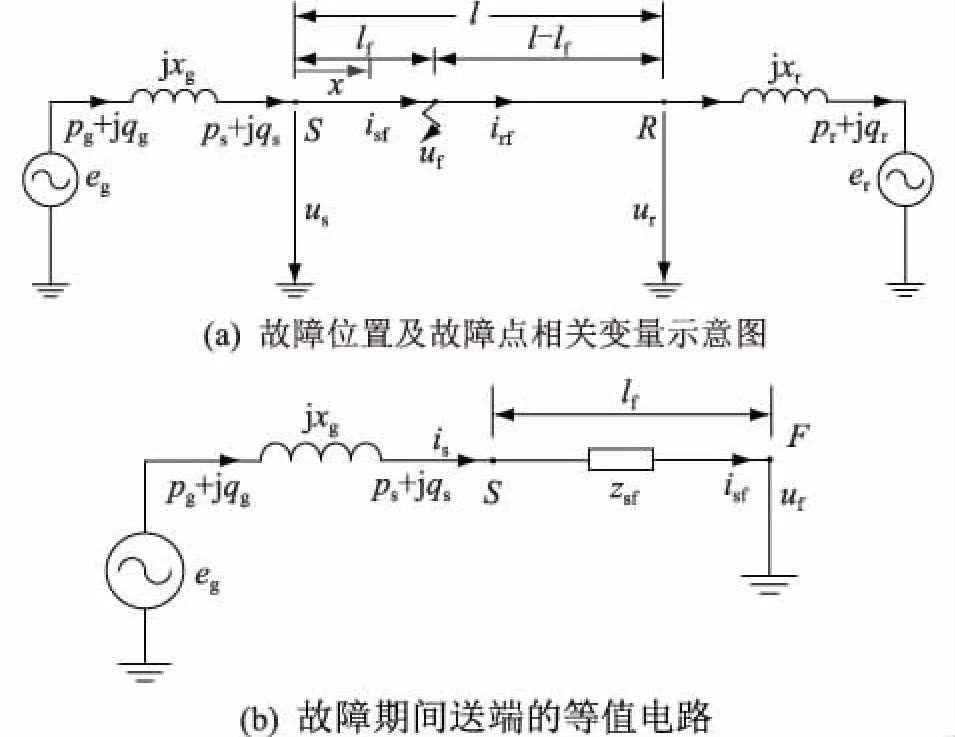
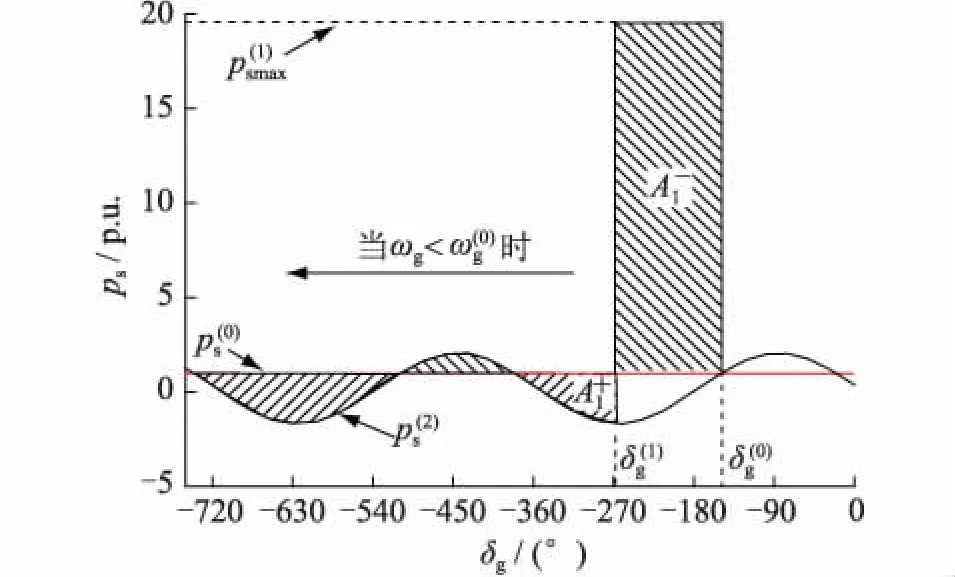
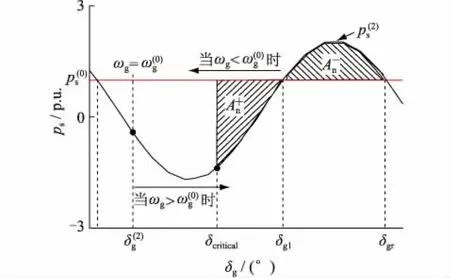
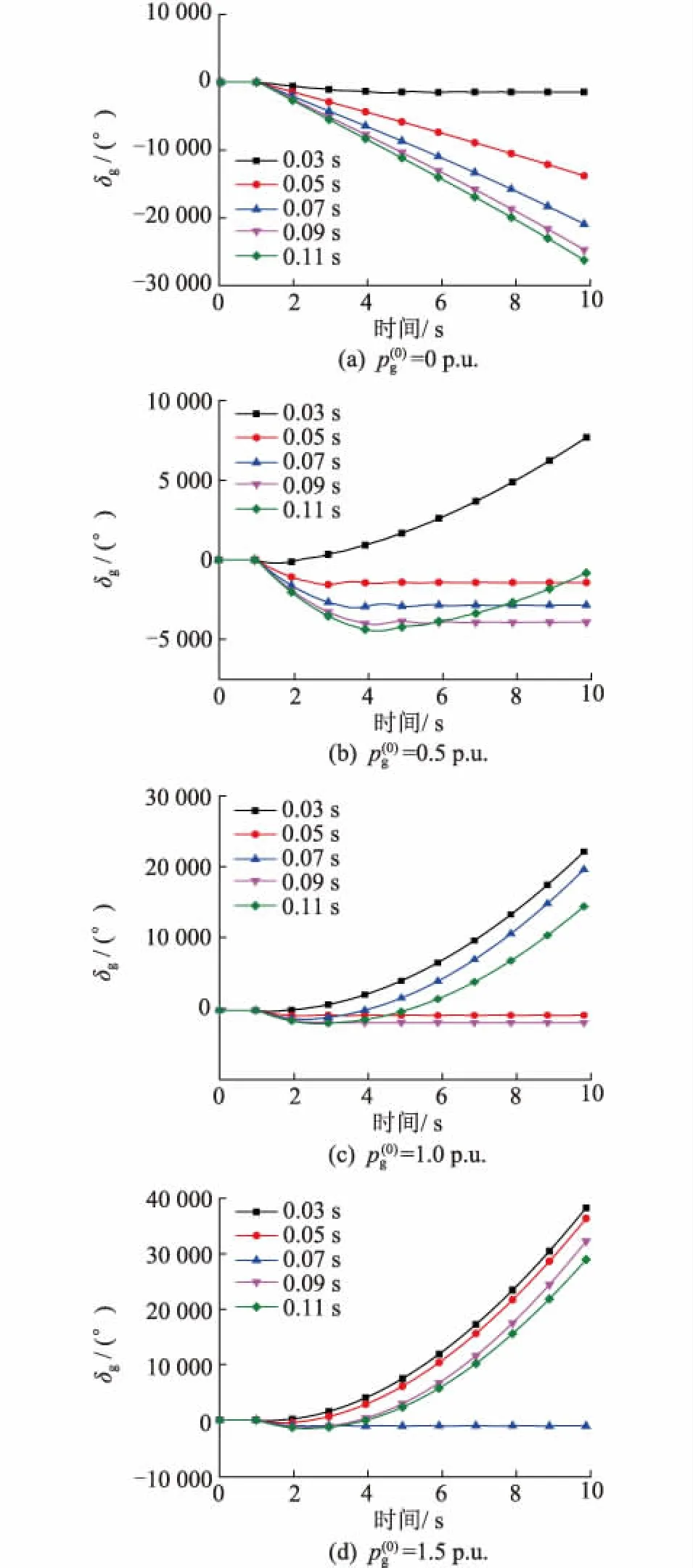
2 862.3 km (32) 当频率偏差取+3%时,能同时满足过电压约束和同步稳定性约束的可行输电距离范围为: 2 695.6 km (33) 2 862.3 km (34) 本节研究半波长输电系统在三相短路故障下的暂态过电压特性。仍然采用第一节中给出的测试系统及暂态模型。假设输电距离在式(34)给出的可行输电距离范围内。t= 0-时系统已处于稳态,故障发生时刻为t= 0+。故障期间系统模型如图7所示。 图7 故障期间系统模型Fig.7 System model under the three-phase short circuit fault 图7中送受端各变量的意义与图1相同。小写字母表示标幺值,其基准值为线路自然功率和线路额定电压;lf为故障点离送端的距离;uf为故障点电压相量;isf和irf为故障点电流相量,方向如图所示。 在波阻抗ZC的相角近似取0的条件下,根据输电线路长线方程并利用短路点电压uf= 0,可得: (35) 则从送端向线路看,输入阻抗zsf为: zsf=us/is=th(γlf) (36) 故障期间,eg的幅值保持不变。根据式(36)和送端等值电路图7(b),可得故障期间送端母线电压和注入电流为: (37) 根据长线方程和式(37),在送端与故障点之间,距离送端x处的电压为: (38) 电压幅值为: (39) 可以证明,当(thγlf+jxg)的虚部等于0时,ux将取到最大值。因此,定义lfmax为Im(thγlf+jxg) = 0的解,其意义为:与其他故障点相比,在lfmax点故障,会导致最严重的过电压。进一步定义最严重过电压出现的位置为xf,umax,其意义为:当三相短路故障发生在故障点lfmax时,最严重过电压(ufmax)出现在xf,umax处。根据上述定义,经过推导可以得到: lfmax=(π-arctanxg)/β (40) xf,umax=lfmax-π/(2β) (41) (42) 从式(40)可以看出,lfmax在离送端不到半波长的位置,并且与eg和er无关。对于测试系统,βlfmax约为168.7°,小于式(34)给出的所有可行输电距离l。这意味着线路上存在某一特定点,其故障将导致最严重的过电压。 根据式(41)可知,发生最大过电压的点刚好在距离故障点1/4波长处。 在PSS/E中进行仿真以验证上述结论。采用图1中的测试系统结构和第1节中给出的系统参数。设定输电距离为3200 km。从线路送端开始,每隔160 km设置一个电压测量点,并依次记为0~20。根据前述分析,当故障点距离送端2 753.4 km时(lfmax= 2 753.4 km),最大过电压(ufmax)将出现在1 284.4 km处(xf,umax= 1 284.4 km),即出现在8号测量点(距离送端1280 km)附近。 在上述故障下,仿真可得系统沿线电压分布如图8所示。 图8 lfmax点故障时沿线电压分布Fig.8 Voltage profile under the three-phase short circuit fault at lfmax 图8中,当pg分别为0 p.u.,0.5 p.u.,1.0 p.u.和1.5 p.u.时,最大过电压(ufmax)分别为22.77 p.u.,22.59 p.u.,22.98 p.u.和23.91 p.u.,且均出现在8号测量点附近,与理论分析结果一致。同时,上述结果表明故障后最大过电压远高于10 p.u.,这在实际工程中是无法接受的。 故障期间,发电机注入线路送端的功率为: (43) (44) 故障期间,发电机的转子运动方程为: (45) 设故障在t=tclear时清除,则在故障清除时刻有: (46) 下面仅针对故障发生在最严重故障点(lfmax)的情况进行分析。若故障发生在lfmax,则故障清除时有: (47) 故障清除后,系统恢复到故障前的结构,发电机的电磁功率表达式与故障前一致,可近似采用无损线条件下的式(10)来表示: (48) 图9 最严重故障下发电机电磁功率与功角的关系曲线Fig.9 Schematic diagram of the generator electromagnetic power 图10 临界角度示意图Fig.10 Schematic diagram of the critical phase angle 可见,发电机在故障清除后或者一直减速,或者减速一段时间后一直加速,无论哪种情况,系统都无法在最严重故障点故障后保持暂态稳定。实际上,即使采用考虑损耗下的电磁功率公式(13),通过类似的分析也可以得到相同的结论。 上述结果表明,在发电机采用恒定电势模型(经典模型)并忽略阻尼作用时,不管输送功率大小,系统在最严重故障点故障后总是暂态失稳的。 下面通过仿真验证上述结论。仍采用前述测试系统,送端发电机采用经典模型,H取8.692 p.u.,D取0;受端系统采用戴维南等效电路,并取xr=0.05 p.u.。仿真过程中,设置1 s时在lfmax处发生三相短路故障,在不同故障清除时间(0.03~0.11 s)下,送端发电机功角变化曲线如图11所示。 图11 送端发电机功角变化曲线(经典模型)Fig.11 The swing curves of the sending-end generator power angle (classical model) 由图11可见,当p(0)g= 0 p.u.时,送端发电机功角δg在故障后持续减小;当p(0)g= 0.5 p.u.,1.0 p.u.和1.5 p.u.时,δg在故障后减小一段时间,之后持续增大。无论是哪种情况,系统在故障后均失稳,这与之前分析得到的结论完全一致。 当发电机采用详细模型并考虑励磁系统作用时(相关参数见附录A2),仿真结果如图12所示。 图12 送端发电机功角变化曲线(详细模型)Fig.12 The swing curves of the sending-end generator power angle (detailed model) 综上所述,当发电机采用详细模型并考虑励磁系统作用时,系统在上述故障下的稳定性是不确定的,取决于故障清除的时间。然而,能够使系统保持稳定的故障清除时间是离散的,系统不存在临界故障清除时间。 针对十九世纪四十年代提出,最近又再次成为研究热点的半波长输电设想,本文采用理论分析与数值计算相结合的方法,进行了深入的分析,主要结论如下: (1) 半波长输电系统存在一个谐振输电距离,该谐振输电距离与送端系统和受端系统的等值电抗有关,与送端系统和受端系统的等值电势无关。该谐振输电距离小于半波长。 (2) 在谐振输电距离下,沿输电线路的最高电压可以达到无穷大。因此,半波长输电系统的输电距离必须要大于谐振输电距离。 (3) 当输电距离小于谐振输电距离时,半波长输电系统是小干扰同步不稳定的。当输电距离大于谐振输电距离时,半波长输电系统是小干扰同步稳定的。 (4) 综合考虑稳态过电压水平、小扰动同步稳定性以及电网实际运行时的频率变化范围3个因素,半波长输电可行的输电距离变化范围是很窄的,对于本文采用的测试系统,可行的输电距离范围约为2900~3300 km。 (5) 半波长输电系统存在一个最严重故障位置,在该故障位置发生三相短路时,距该故障位置四分之一波长处,出现最严重过电压,数值大于10 p.u.。 (6) 在最严重故障位置发生三相短路时,若发电机采用经典模型并忽略阻尼,则不管故障切除时间和初始输送功率为多少,系统总会失去暂态同步稳定。 (7) 在最严重故障位置发生三相短路时,若发电机采用详细模型并考虑励磁控制系统的作用,则系统的暂态同步稳定性是不确定的,与故障切除时间和初始输送功率没有确定的关系。 (8) 由于半波长输电系统的暂态工频过电压超过10 p.u.并且暂态同步稳定性不能得到保证,因此半波长输电的设想是不能成立的,半波长输电没有工程可行性。6 暂态过电压分析


7 暂态稳定性分析

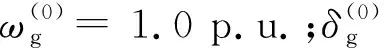

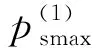




8 结论
