多层次电压暂降评价方法研究

2018-12-12浦天宇

电力工程技术 2018年6期

张军，浦天宇

(1. 国网江苏省电力有限公司,江苏南京 210024； 2. 南京航空航天大学自动化学院，江苏南京 211106)

0 引言

随着计算机应用技术和自动控制技术的飞速发展，大量基于计算机和微处理器管理、分析、检测和控制的新型电气设备已经投入到电力系统的使用中。这些高性能、高度自动化的电力电子设备对系统干扰非常敏感，因此电能质量成为电力部门和用户关注的焦点。电压暂降造成的经济损失是电能质量中最严重的问题之一[1-5]。统计分析表明，典型生产线电压暂降造成的损失从几万美元到几十万美元不等。大型连续生产企业每年因电压暂降造成的经济损失可达数千万美元。

IEC、IEEE等国际组织对电压暂降指标进行了广泛的研究。IEEE P1564为电压暂降评估系统提出了一个包含5个步骤的框架，充分反映了暂降事件本身、用户、监控和系统对暂降事件的影响。文献[6]通过改进的层次分析法(improved analytic hierarchy process， IAHP)和矢量标幺化的方法，提出了一种综合考虑电力系统和用户设备的电压暂降严重度指标。该文献在充分考虑供电和用户两方面因素的基础上，采用该指标对典型的110 kV变电站的电压暂降严重程度进行评价。文献[7]通过分析各种指标来估计单次事件电压暂降严重度，提出了一种将暂降的严重程度进行分类的方法，并将严重程度指标与参考值进行比较。文献[8]在IEEE P1564 给出的电压暂降评价方法的基础上，对国内外文献中探究的电压暂降评价指标进行整合，提取特征值，分析优缺点，并对其中一些指标进行了改进，给出了多步骤评估方法。文献[9]详细总结分析，比较了IEC、IEEE 等国际组织以及国内外相关文献中给出的相关暂降指标，并且依据电压暂降指标描述的不同特征将其归纳分类。同时该文献对其中的系统平均均方根频率指数(system average RMS variation frequency index, SARFI)指标、暂降模糊指标、能量指标、中断时间指标以及一些经济损失评价指标等的应用场合和优缺点进行了讨论，对相关指标进行优化。文献[10]总结了多种电压暂降严重程度评价指标与评估方法；结合供电侧、输电侧、用户侧多方的危害程度、影响因素、要求与特点，探究了电压暂降严重程度的评价测度存在条件，按照不同层面的数学和物理特性，从多方面分析暂降严重程度评价指标与体系。

目前常用的电压暂降严重度评价指标主要是由国际组织IEC和IEEE提出的[11-13]。然而这些指标对每个监测站的评价不够全面。此外，由于持续时间和暂降幅值是电压暂降的关键特征值，现有的研究结果并没有合理地考虑这两者的相对权重。本文以电网电能质量监测系统中单次暂降事件和监测节点为研究对象，提出了一种基于IAHP和熵权法的多层次电压暂降评价方法，该方法从暂降事件和监测节点的角度出发，分层次考虑了电压暂降持续时间和暂降幅值这两个特征值，可以定量评价电压暂降的实际严重程度。

1 传统电压暂降统计指数

1.1 SARFI

NSARFI用来表示电力公司在电压均方根值变动上的服务质量[14-15]。一般包括两种形式:NSARFI,x和NSARFI,curve。其中NSARFI,x是一种针对某一阈值电压的统计指数，可以按式(1)计算:

(1)

式中：x表示电压暂降阈值的方均根值；Ni为第i个电压暂降电压幅值小于x%的用户数量；NT为用户总数。针对暂降持续时间的不同可以将NSARFI,x分为瞬时指标NSIARFI,x，暂时指标NSMARFI,x和短时指标NSTARFI,x。NSARFI,curve是统计电压暂降事件超出国际技术工业委员会容忍度曲线电压包络线所定义的区域的频数。

由此可见，NSARFI值与电压暂降严重程度成正比。然而，该统计值不包含暂降持续时间和暂降幅值的影响。因此，单用NSARFI值并不能准确评价电压暂降严重程度。

1.2 用户平均暂降事件次数指标

用户平均暂降事件次数指标(average sag event times of customer ,ASTC)表示单位时间内，每个受电压暂降影响的用户经历的暂降事件次数的平均值[16]，可以由下式表示：

(2)

式中：U为敏感性曲线上设备电压暂降承受值；NSTC,U,i表示单位时间内第i个用户经历的暂降事件次数；NE表示电网系统内发生电压暂降事件的用户总数。该统计值与NSARFI值含义类似，同样无法准确评价暂降事件严重度。

1.3 暂降能量指标

暂降能量指标EVS表示电压暂降事件的能量，可采用下式计算[17]：

(3)

式中：U(t)为电压暂降过程中电压的方均根值；Unom为标称电压；积分时间长度T为电压暂降的持续时间。特别地，当电压暂降出现在多相时，该能量定义为各相暂降能量之和：

EVS=EVS-A+EVS-B+EVS-C

(4)

式中：EVS-A，EVS-B，EVS-C为各相暂降能量。

但该指标只能反映单次暂降事件的严重程度，未能体现持续时间与暂降幅值的相对重要性，较为片面。

1.4 严重性指标

反映暂降严重性的暂降幅值严重度指数 (IMSI)、暂降持续时间严重度指数 (IDSI)和暂降幅值和持续时间严重度综合指数 (IMDSI)分别从幅值和持续时间两个方面，反映了由电压暂降事件对设备的干扰程度。由下式可得:

(5)

(6)

(7)

式中：t和Um分别为该次电压暂降的持续时间和暂降幅值。tmin，tmax，Umin和Umax分别为电压暂降容忍度曲线上的持续时间与暂降幅值，如图1所示。图中P区域代表该暂降事件不会造成设备故障，Q区域表示该暂降事件可能造成设备故障，R区域表示该暂降事件肯定造成设备故障。

图1 电压暂降容忍度曲线Fig.1 Tolerance curve of voltage sag

同样地，这3个指标仅反映了一次电压暂降持续时间和暂降幅值的严重性，并不能反映电网中典型监测站所有暂降事件的严重程度。

2 多层次电压暂降评价方法

对于单次的电压暂降事件评价可以预估该事件造成的危害严重程度；对于监测站点进行评估可以分析某区域暂降严重度的分布情况，为进一步治理作准备，因此必须建立多层次的电压暂降评价方法。

而对于电压暂降事件而言，有两个基本特征值：持续时间和暂降幅值。这两个关键量从不同的方面衡量暂降事件的严重程度，因此需要综合考虑。AHP是一种将复杂系统分解为多目标决策问题，通过定性指标模糊量化计算权重的决策方法，可以较好地运用于电压暂降严重度评价中。但是传统的AHP分析指标较多，数据统计量大，且权重难以确定，而IAHP 采用拟优传递矩阵构造判断矩阵，无需进行一致性检验，计算复杂度较低。此外，为客观评价持续时间和暂降幅值两者的相对重要程度，可以采用熵权法求出两者的权重。熵权法是一种客观的权重确定方法，用来衡量评价系统中指标的有效信息，进一步可计算指标的权重值。因此，整个多层次评价方法如图2所示。

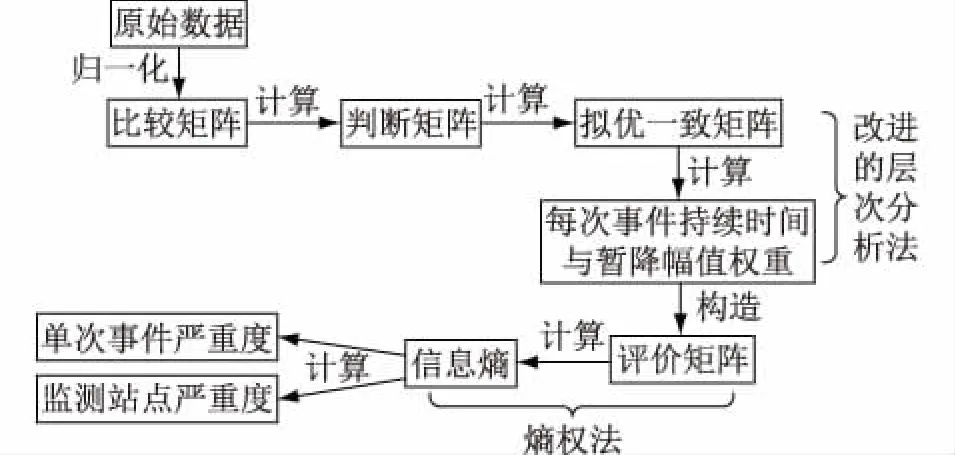
图2 多层次电压暂降评价方法示意Fig.2 Schematic diagram of the multi-level evaluationmethod

2.1 IAHP

AHP是指将与决策相关的指标分解成目标、方案、准则等层次，在此基础上进行定性和定量分析的决策方法。通常该方法采用九标度法比较两个指标之间的相对重要程度，从而导致其规模复杂、一致性验证困难，本文采用一种IAHP方法。与传统方法相比，有以下优点:

(1) 用五标度法代替九尺度法，降低了标度的复杂性和计算量[18]。

(2) 利用拟优传递矩阵构造判断矩阵，无需进行一致性检验[19]，减小运算量。

由于持续时间和暂降幅值对电压暂降严重程度的影响是明确的，因此可以建立一个准确的相对重要性判断矩阵。

以持续时间为例，根据其两两之间的大小关系，设置合理的标度，表1为其相对重要性标度。

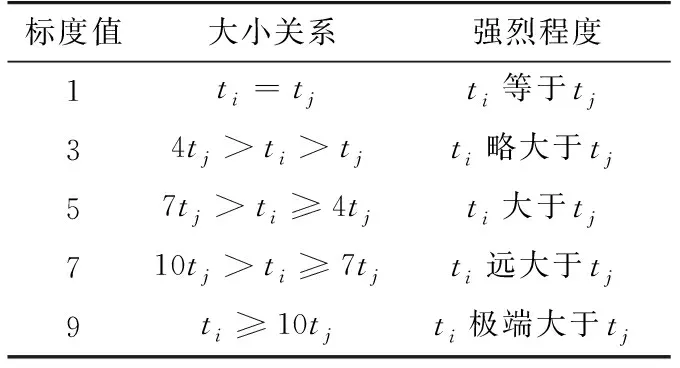
表1 持续时间比较矩阵的相对重要性标度Tab.1 Relative Importance Measurement of Comparison Matrix

表中ti和tj分别是两次暂降事件的持续时间。IAHP的具体步骤如下:

(1) 比较矩阵可由表1得到，如下式所示:

(8)

其中，当ti≥tj时，cij是表1中的值，当ti

(2) 计算比较矩阵重要性的排序指数：

(9)

(3) 求出持续时间判断矩阵MJ，其元素为：

(10)

式中：rmax=max{r1,r2,…,rn} ,rmin=min{r1,r2,…,rn}。

(4) 构建持续时间判断矩阵的拟优一致矩阵Mq，其元素为：

(11)

式中：aij=lgJij。

(5) 构建矩阵Tij，其元素为：

(12)

(6) 计算权重向量，可由式(12)中的元素得到：

(13)

最后，得到每次电压暂降事件持续时间的权值，即权向量。采用同样的方法可以计算得到每次电压暂降事件暂降幅值的权值。

2.2 熵权法

上述IAHP得到的是每次暂降事件持续时间暂降幅值各自的权重，而对于两者的相对重要性，本文采用熵权法计算。相比较于IAHP方法专家打分的随机性，熵权法通过各特征数据的值来确定电压暂降的严重程度，是一种客观赋权法，运算量适中，计算精度高。计算方法步骤如下:

(1) 采用基于持续时间和暂降幅值的权向量构造评价矩阵：

(14)

式中：Wt和Wv为IAHP方法通过式(8—13)得到的权向量。

(2) 根据评价矩阵计算持续时间和暂降幅值的信息熵：

(15)

式中：dpq为式(14)评价矩阵中的矩阵元素。特别的，当dpq=0，dpqlndpq=0。

(3) 将持续时间和暂降幅值两者的权重定义为：

(16)

式中：ω1和ω2分别为电压暂降时持续时间和暂降幅值的权重指数，即相对重要度。

2.3 单次暂降事件严重度评价方法

针对单次电压暂降事件，本文提出了一种加权欧式距离法进行严重度评价，如图3所示，综合考虑持续时间与暂降幅值对严重度的影响，其计算公式为：

(17)

式中：U为本次电压暂降幅值；U0为容忍度曲线上确保设备正常运行的最大电压值；T为本次电压暂降持续时间；T0为容忍度曲线上确保设备正常运行的最短持续时间。为确保设备可靠工作，可选择可调速驱动器的容忍度曲线，其电压暂降最短持续时间为10 ms，最长为175 ms，标幺化后的暂降幅值最大为0.45，最小为0.1。

图3 加权欧式距离法严重性评价示意Fig.3 Schematic diagram of severity evaluation of weighted Euclidean distance method

同时建立多级严重度评价方法，包括一级严重度(C<0.06) ，二级严重度(0.06≤C<0.12)，三级严重度(0.12≤C<0.18)，四级严重度(0.18≤C)和特级严重度(该事件处于设备故障区)，其中C为该次电压暂降的加权欧式距离。通过加权欧式距离与阈值比较得到相应的严重度等级。若该暂降事件处于正常工作区，则无需进行严重度等级判断。

2.4 监测站点电压暂降严重度评价方法

对于某监测站点评价，需要考虑一段时间内该站点监测到的电压暂降事件的相关特征量，包括暂降频数，持续时间与暂降幅值。因此针对监测站点，本文提出了一种综合评价指标(comprehensive evaluation index ,CEI)，将IAHP与熵权法相结合，给出了某监测站电压暂降严重程度的综合评价指标。第i个监测站点的CEI指数ICEI,i可以表示为：

(18)

式中:n为某段事件内该监测站监测到的电压暂降事件总数;ICEI,i,j为第i个监测站的第j次电压暂降严重指数，由下式计算:

ICEI,i,j=ω1ITEI,i,j+ω2IVEI,i,j

(19)

式中:ITEI,i,j，IVEI,i,j分别为第i个监测站第j个电压暂降严重指数持续时间和暂降幅值的权重，即式(13)中权向量的元素。

CEI指数不仅反映了持续时间和暂降幅值对电压暂降严重程度的影响，而且考虑了一段时间内该监测站点电压暂降事件的总数。与传统的统计指标相比，用CEI指标评价监测站点电压暂降的严重程度更为合理。