基于三型补偿网络的开关电源电压控制研究

郭勇

(赣南师范大学 物理与电子信息学院，江西 赣州 341000)

0 引 言

开关电源具有可靠、高效和小型等特点。文献[1]指出将其应用于智能变电站，给继电保护、自动控制装置和事故照明等提供可靠动力，能够满足稳定、可靠和高效等要求。文献[2]设计了四路输出ZCS-PWM反激式开关电源，为轨道车辆的控制部分、驱动部分及各种采样电路等供电，具有轻量化、效率高等特点。在开关电源的设计中，输出电压稳定是重要的控制指标。传统的控制方法主要采用PI和PID控制器。文献[3]通过空间状态法分析建立了全桥变换器的小信号模型，并设计了基于 PI 控制的电流型双闭环(电流内环，电压外环)控制系统。此外，二型补偿网络和三型补偿网络也被运用于控制器设计中。文献[4]采用峰值电流模式控制设计二型补偿网络，应用于反激式开关电源中，满足了输出电压的快速调节性和稳定性。文献[5]为反激式开关电源设计了二型补偿网络，通过频率响应分析仪获得系统的开环波特图，再精确设计补偿网络的零、极点，使系统稳定且具有较好的动态响应能力。文献[6]为buck拓扑设计了3A型补偿网络，考虑滤波电容的ESR零点进行补偿网络的零、极点设计，指出通过改变补偿网络外部电容Cff调节相位裕度，以满足电压模式buck变换器的环路设计要求。文献[7]为循环恒温冷却水系统中的半导体制冷器设计了全桥式开关电源进行驱动，采用三型补偿网络，使电压控制线性度达到0.44%。综合比较而言，采用补偿网络的设计方法能够对变换器的零、极点进行补偿，得到系统所需的开环波特图，易于获得满意的性能指标。

本文采用电压模式控制策略，分析三型补偿网络(双极点-双零点PI补偿网络[8])在正激式开关电源中的应用。通过给定对象的具体参数以及补偿网络的零、极点，改变其比例系数K，运用MATLAB仿真，得到该补偿网络在不同比例系数K下系统的稳定性、动态性能、抗输入扰动能力以及抗负载扰动能力等方面的变化情况，从理论分析和仿真的角度验证该补偿网络在兼顾提高系统各方面性能的正确性和有效性。

1 电压控制策略分析

1.1 电源总体结构

本文以正激式开关电源为例，对补偿网络进行分析和系统仿真。正激式开关电源电压模式控制结构如图1所示。图1中，VIN为正激变换器的直流输入电压，VEA_OUT为补偿网络的输出电压。

1.2 三型补偿网络分析

三型补偿网络电路图如图2所示。它具有2个零点、3个极点(其中一个是零极点)。

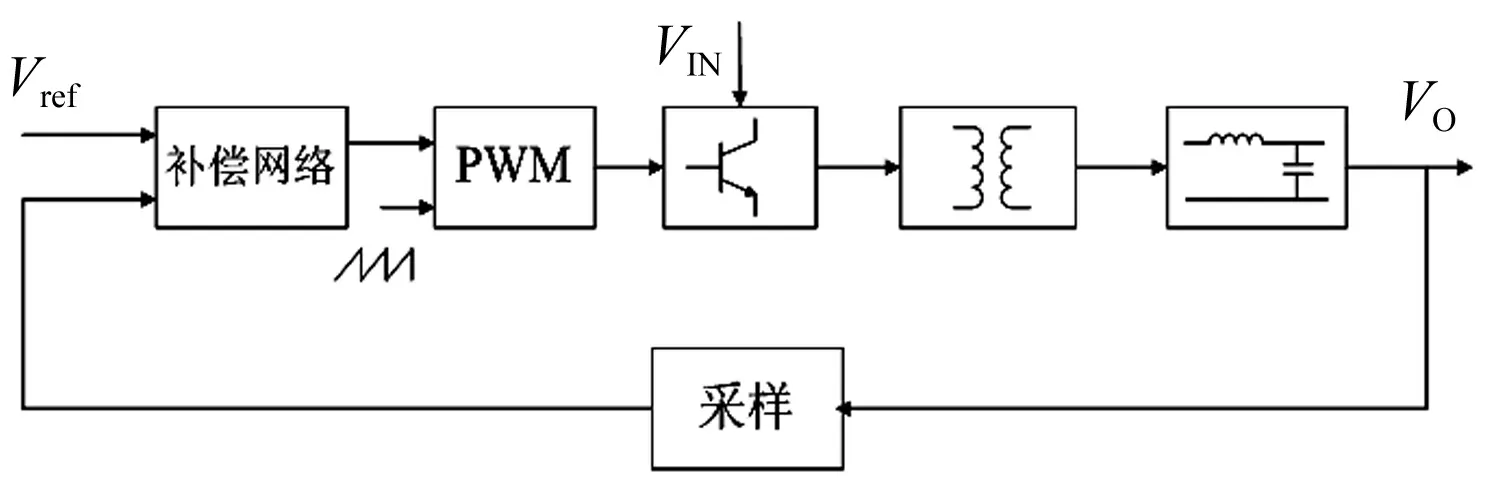
图1 正激式开关电源电压模式控制结构图

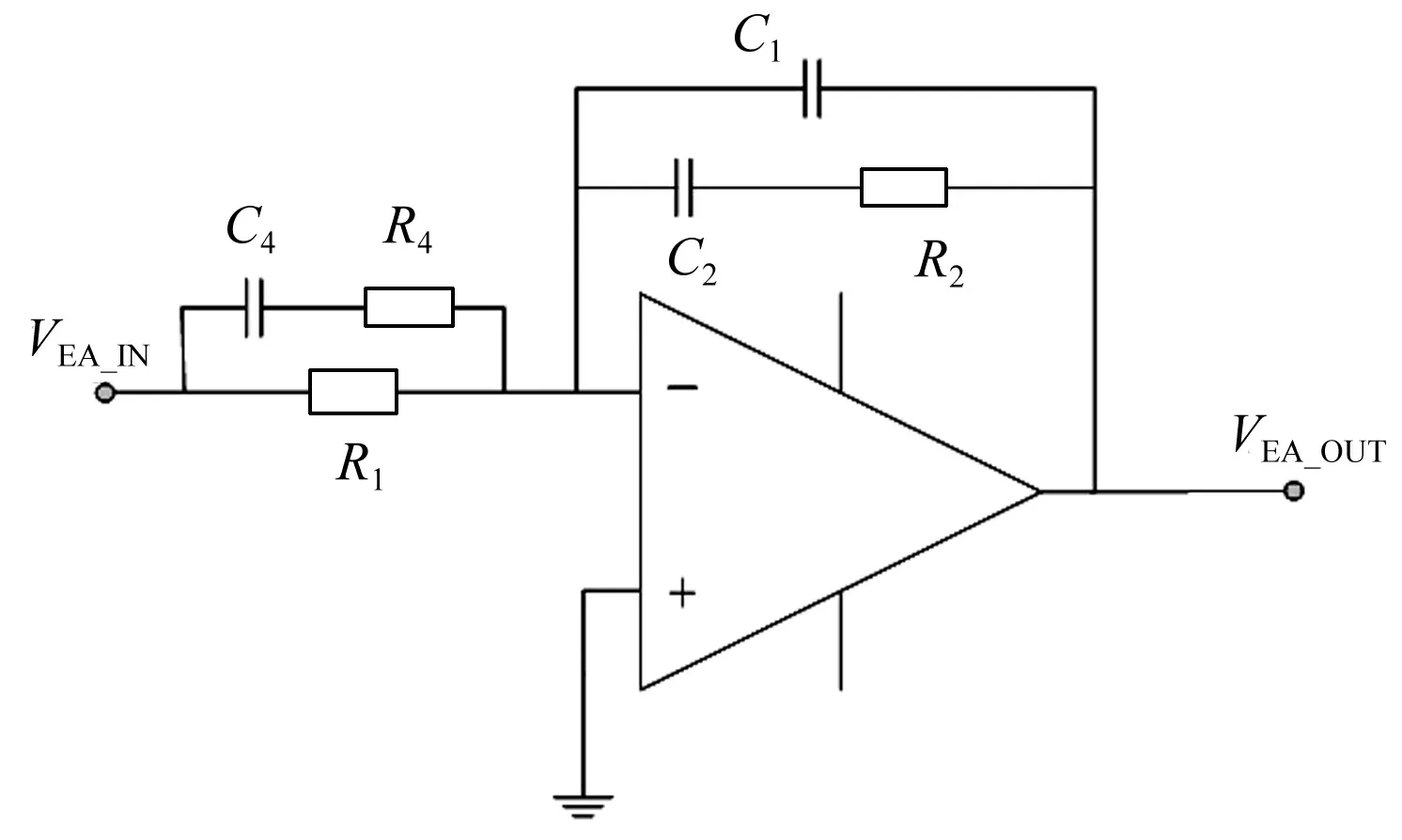
图2 三型补偿网络电路图

图2中，VEA_IN为补偿网络的输入电压，也即控制系统的输入与输出电压采样值的差值，VEA_OUT为输出电压。对图2计算补偿网络的传递函数如式(1)所示。

(1)

式中：R1、R2、C1、C2、C4对应图2中各元件。

1.3 系统控制策略

假定输出电压采样比例为1，由图1得到控制系统的结构框图，如图3所示。

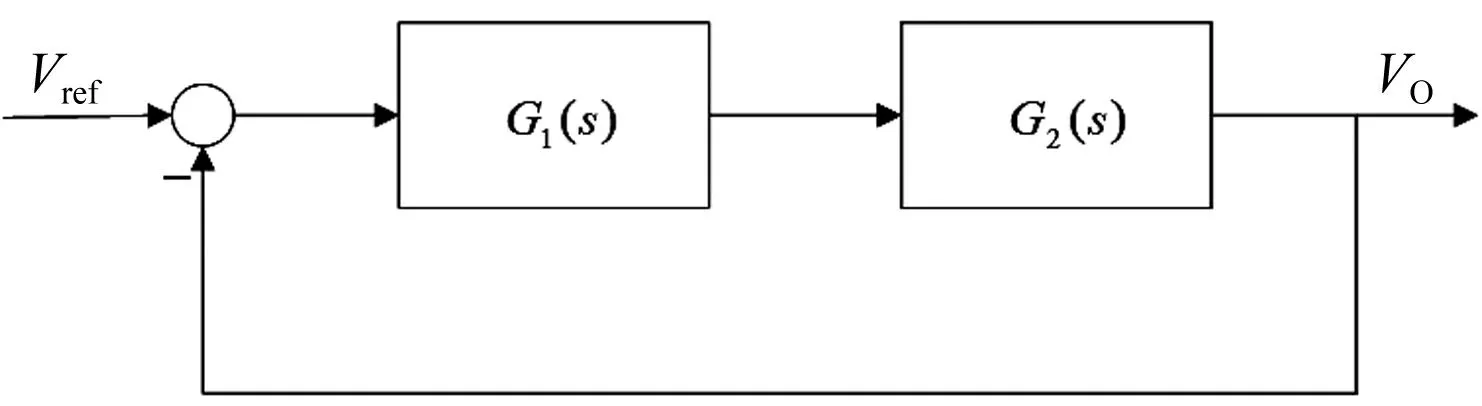
图3 控制系统的结构框图

图3中，G2(s)为从补偿网络的输出VEA-OUT到系统输出Vo的传递函数，如式(2)所示。

(2)

式中:R为系统的负载电阻，包括假负载RL在内;VIN为输入直流电压;Vromp为锯齿波的幅值。

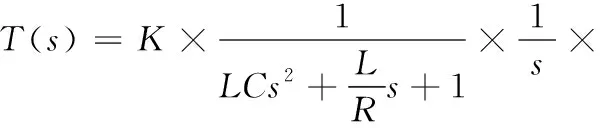
(3)

在设计系统的补偿网络时，期望系统的低频增益很大，以增强抗输入扰动能力；中频段以-1的斜率下降，增大系统的带宽，以提高系统的动态响应能力；提高高频段的斜率，以衰减高频噪声，尤其是开关噪声。三型补偿网络恰好提供了所期望的极点和零点，从而使系统的性能得到提高。

在开关电源中，设输入为Ui，输出为UO，假负载为RL，流过负载R的电流为IO，关系式见式(4)。

(4)

结合补偿网络的传递函数，考虑抗负载扰动能力时系统结构框图如图4所示。

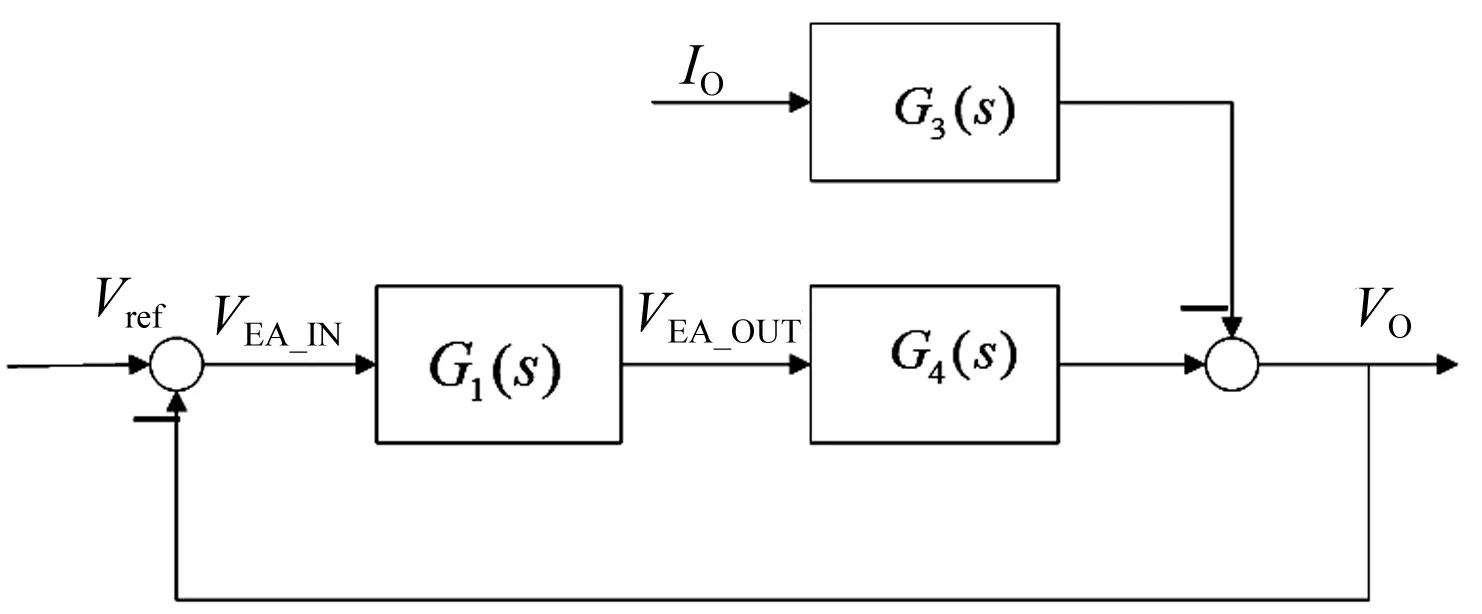
图4 考虑抗负载扰动能力时系统结构框图

由图4可以看出，系统的开环传递函数保持不变。

2 仿真与分析

2.1 基本参数设置

本文以正激式开关电源为例，电源的具体参数为：①输入电压VIN为DC 264 V；②输出电压VO为DC 0～36 V；③输出电流IO为0～2 A；④开关频率f0为40 kHz；⑤变压器变比N为2:1；⑥输出电感L为0.9 mH；⑦输出电容C为100 μF；⑧锯齿波幅值Vromp为5 V。

根据零、极点配置原则，选定补偿网络的极点和零点分别为ωp0=0，ωp1=4.191×105rad/s，ωp2=4.191×106rad/s，ωz0=1 000 rad/s，ωz1=6 000 rad/s。

2.2 系统的稳定性和抗输入扰动能力仿真

根据图3搭建MATLAB仿真框图，分别设置比例因数K=1.5×1010、1.5×109和1.5×108，同时考虑系统不同运行情况(带不同负载R=500、18、0.5 Ω)，考察系统的稳定性能和抗输入扰动能力。通过计算不同参数下系统的开环传递函数，绘制bode图，得到不同比例因数K的系统性能，如表1所示。

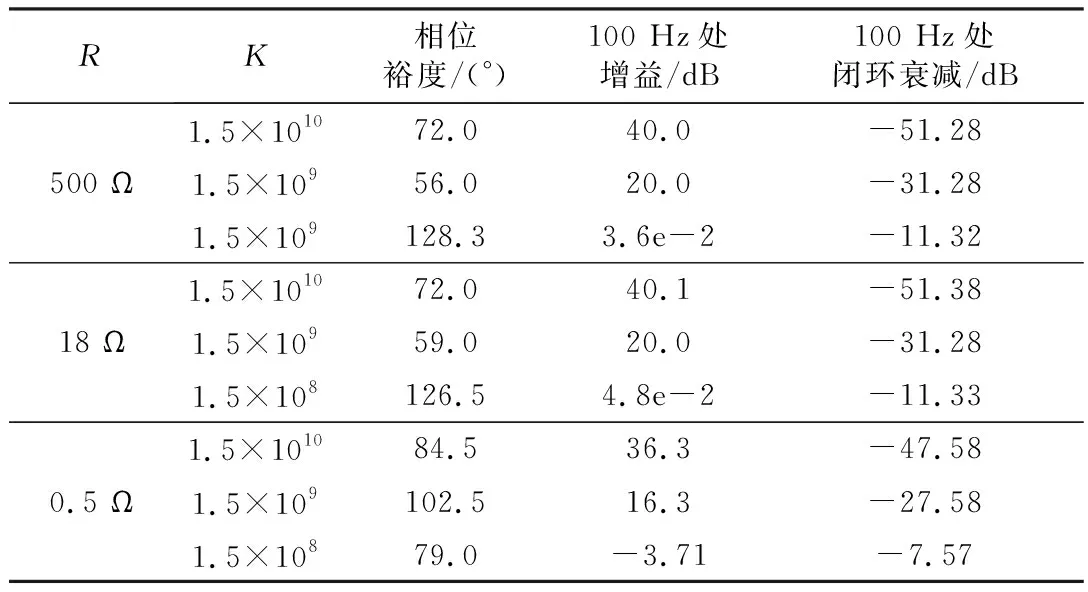
表1 不同比例因数K的系统性能比较

从表1可以看出：

(1)系统总体都是稳定的，而且有比较大的稳定裕量；

(2)比例因数K越高，100 Hz处的增益越大，100 Hz处闭环衰减越严重；

(3)系统的运行情况不同，同等条件下系统性能有所不同，但差异不大。

为了更加直观地描述系统的性能，设置系统的比例因数K=1.5×1010，考虑系统不同运行情况(带不同负载R=500、18、0.5 Ω)，通过仿真得到系统的阶跃响应曲线。K=1.5×1010时不同运行情况的阶跃响应曲线如图5所示。由图5可知，系统的动态性能很好，并且差异不大。负载电阻R=0.5 Ω，由于相位裕度较大，调节时间稍长，而超调量较小。两条曲线基本重合，分别对应R=500 Ω和R=18 Ω的情况。

由图5可知，由于开环传递函数含有积分环节，系统的稳态误差为0，超调量和调节时间达到满意效果。

2.3 系统的抗负载扰动能力仿真

根据图4搭建仿真模型，分别设置系统的比例因数K=1.5×1010、1.5×109和1.5×108，单独考察负载电流扰动对系统的影响。令Vref，负载电流从0到2A阶跃变化，负载电流阶跃扰动单独作用对系统的影响曲线如图6所示。

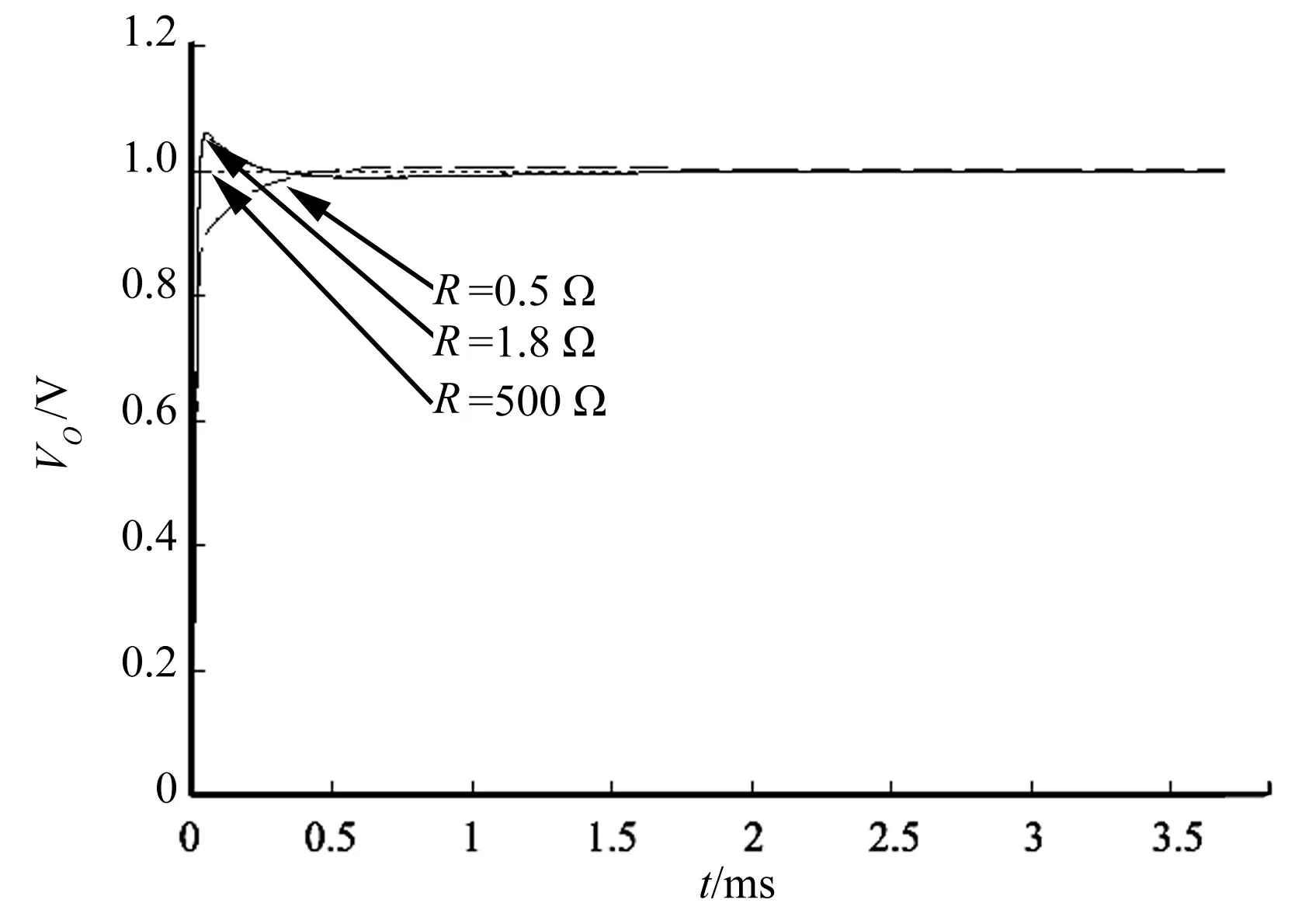
图5 K=1.5×1010时不同运行情况的阶跃响应曲线

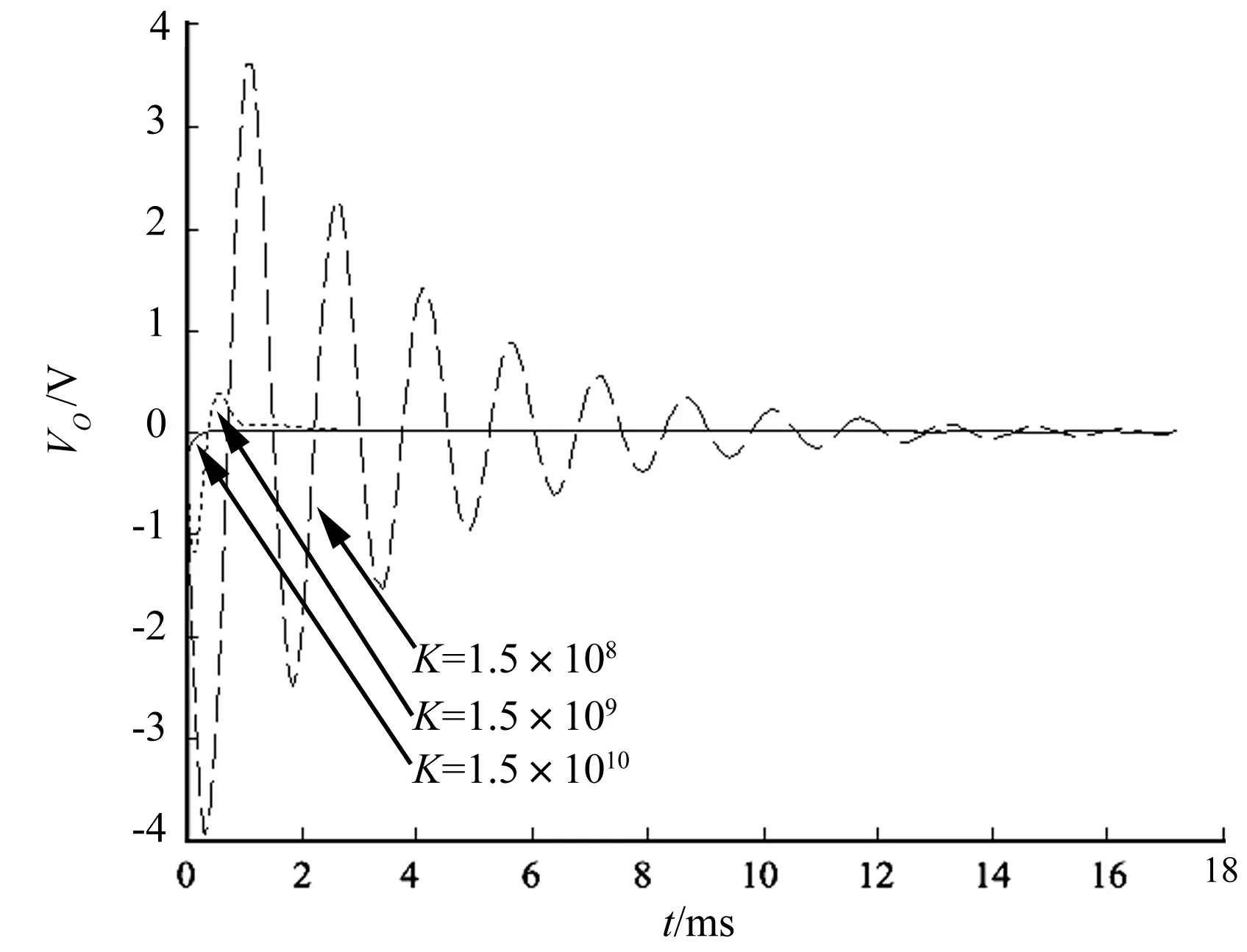
图6 负载电流阶跃扰动单独作用对系统的影响

图6中三条曲线分别对应K=1.5×1010、1.5×109和1.5×108。可以看出：

(1)在三种不同的比例因数下，负载电流阶跃扰动对系统的影响最终为0；

(2)比例因数K越大，系统的输出到稳态为0的调节时间越短，振荡越小。

分别设置系统的比例因数K=1.5×1010、1.5×109和1.5×108，考察负载电流阶跃扰动后系统的单位阶跃响应，取Vref，负载电流从0到2A阶跃变化，负载电流阶跃扰动下系统单位阶跃响应曲线如图7所示。

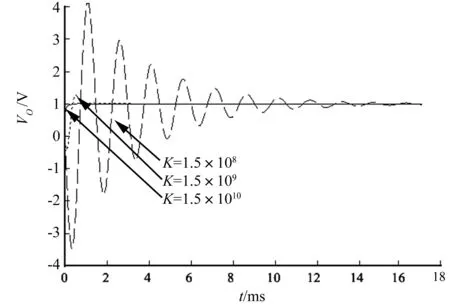
图7 负载电流阶跃扰动下系统单位阶跃响应曲线

图7中三条曲线分别对应K=1.5×1010、1.5×109和1.5×108。由图7可以看出，在负载电流阶跃扰动下，系统的阶跃响应与负载电流阶跃扰动单独作用时变化趋势一致。

3 结束语

综上所述，由于三型补偿网络能够提供两个零点和三个极点(含一个零极点)，在开关电源控制器设计中，通过适当配置零点和极点的位置，改变比例因数K，提高低频增益，增大系统带宽，抑制高频干扰，不仅使系统稳定裕度高，稳态误差为0，而且提高了系统的抗输入扰动能力和抗负载扰动能力，通过MATLAB仿真验证了补偿网络在上述性能表现上是正确和有效的。