基于准PR控制器和陷波器的H6拓扑单相并网逆变器研究

黄冠， 殳国华， 周清文

(上海交通大学 电子信息与电气工程学院，上海 200240)

0 引 言

两级式单相非隔离光伏并网逆变器具有效率高、体积小和成本低等特点，在分布式光伏发电领域得到广泛应用。由于传统H4拓扑不具备漏电流抑制能力，国内外学者提出一些新型拓扑，如H5拓扑、H6拓扑和Heric拓扑等，其中H6拓扑能够有效抑制漏电流，具有总谐波畸变率(Total Harmonics Distortion, THD)小和效率高等优点，且不存在专利封锁。

光伏并网逆变器常用的控制算法有：比例积分(Proportional Integral,PI)控制、电流滞环控制、重复控制和比例谐振(Proportional Resonance,PR)控制等。PI控制控制原理简单、可靠性高，但无法实现对正弦参考信号零稳态误差跟踪；电流滞环控制稳定性好、动态响应速度快、简单易于实现[1]，但其开关频率不固定。重复控制可以对周期性信号进行无静差跟踪，但其动态性能较差[2]。PR控制虽然能够在基波频率处实现零稳态误差控制，但其易受电网频率波动影响。本文将准PR控制引入到电流内环控制中，准PR控制既保留了PR控制在基波频率处的高增益，同时对电网频率波动的敏感度较低。

由于逆变器输出电压、电流同频同相，输出功率除含有直流项外，还含有二次谐波项，此二次谐波项造成直流电压出现二次纹波，而这个二次纹波将导致并网电流中出现严重的三次谐波，并导致并网电流THD增大。通过在电压外环引入陷波器(Bandstop Filters,BSF)，可有效抑制并网电流中的三次谐波。

1 H6拓扑结构及工作原理分析

1.1 主电路拓扑

H6拓扑结构如图1所示，S1～S4为高频开关管，S5、S6为低频开关管，D1、D2为续流二极管，L1、L2为滤波电感，C1为滤波电容，Cdc为直流母线电容。功率电路参数如表1所示。

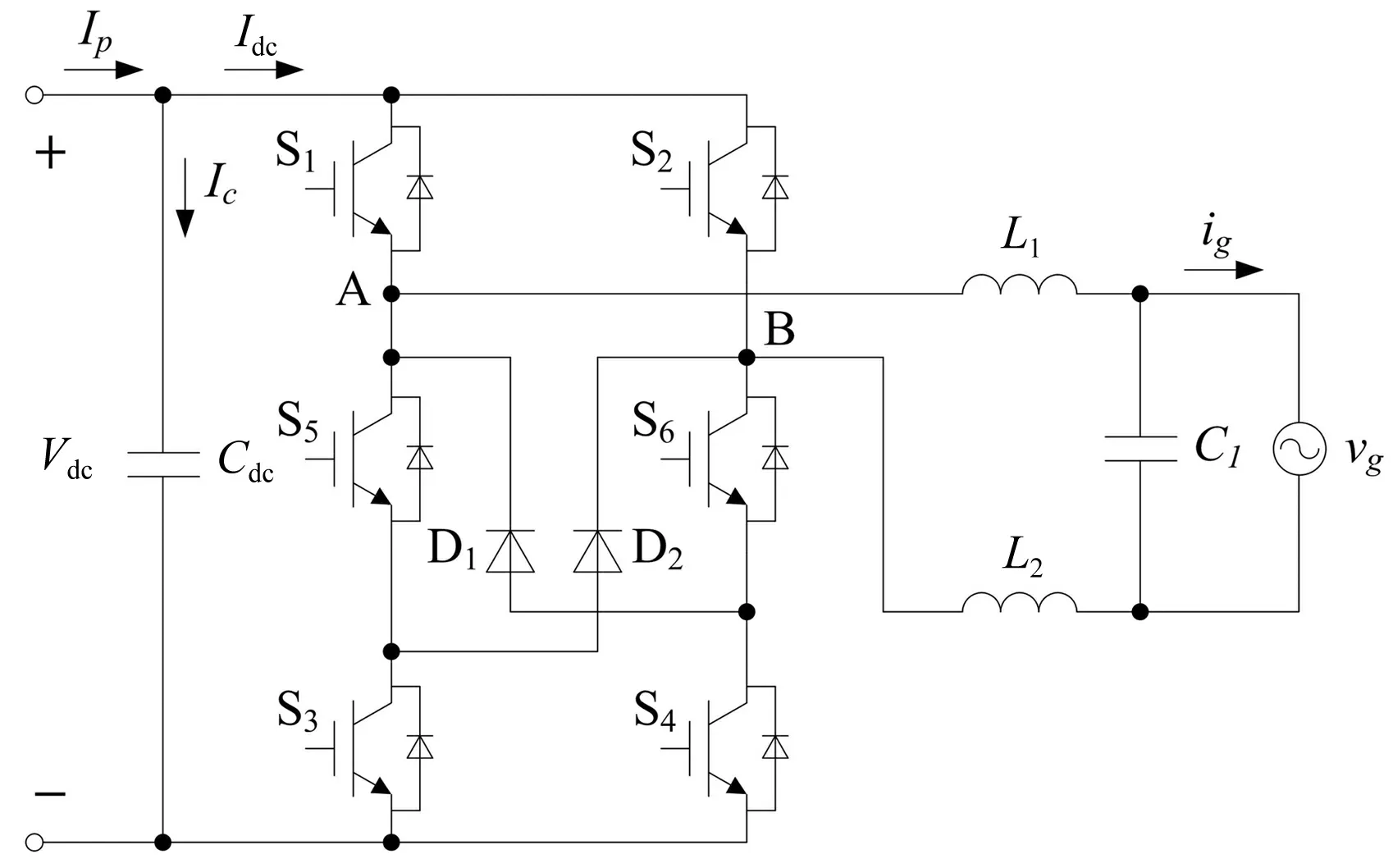
图1 H6拓扑结构

H6逆变桥驱动信号如图2所示，vcon为正弦调制波，vcar为三角载波，G1～G6分别为开关管S1～S6驱动信号。H6逆变桥采用单极性正弦脉宽调制(Sinusoidal Pulse Width Modulation,SPWM)调制，G1～G4由三角载波和正弦调制波比较得到，只在半个周期工作，G5、G6工频导通关断。

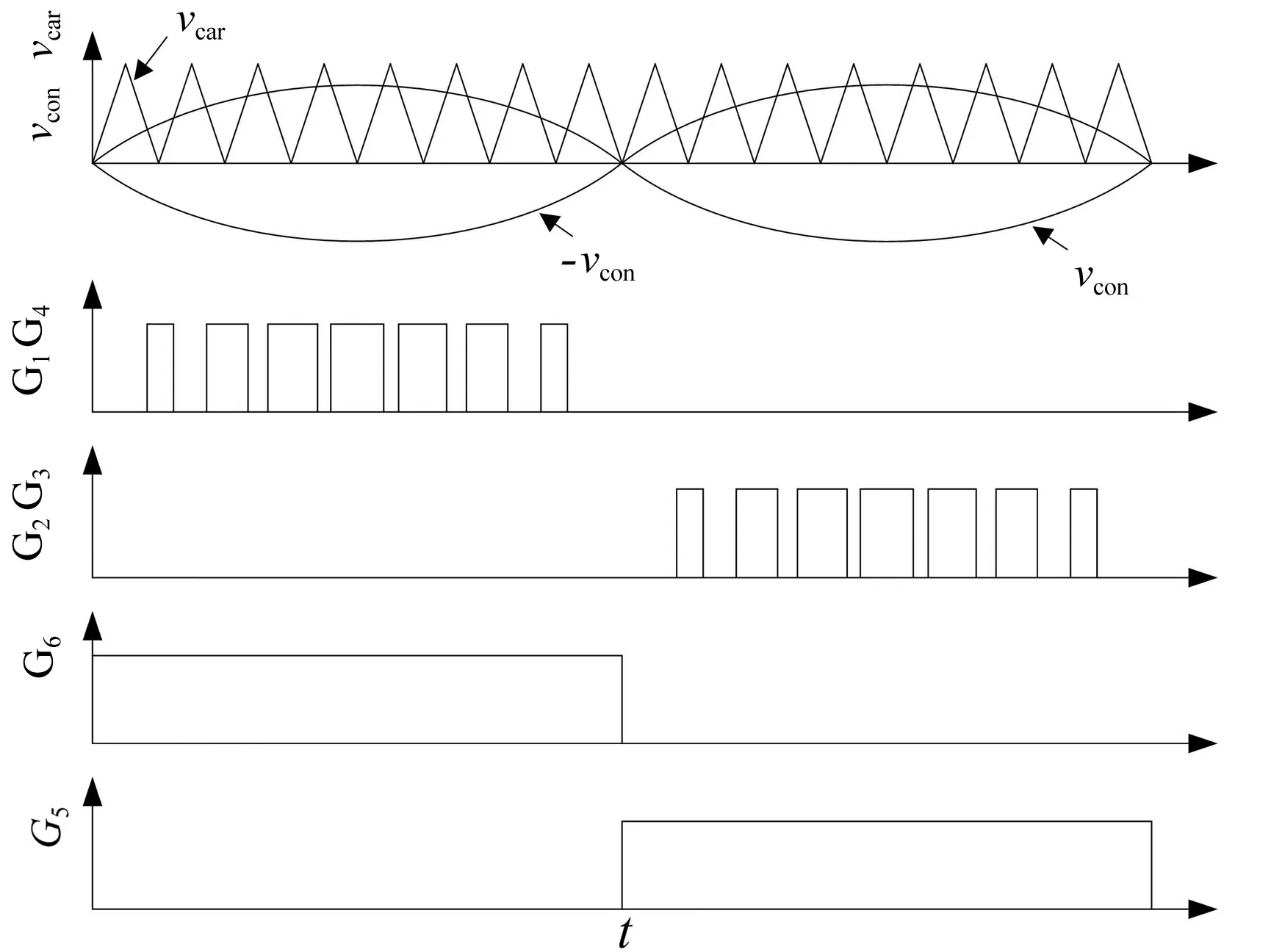
图2 H6逆变桥驱动信号

参数数值电网电压Vg/V220电网频率fg/Hz50开关频率fs/kHz18直流母线电压V*dc/V380直流母线电容Cdc/μF2410滤波电感L1/mH1.4滤波电感L2/mH1.4滤波电容C1/μF4.7

1.2 H6拓扑工作原理

以市电正半周期为例，S2、S3、S5常断，S6常开。当S1、S4导通时，电流通过开关管S1→滤波电感L1→电网→滤波电感L2→开关管S6→开关管S4构成回路，电感电流正向上升；当S1、S4关断时，电流通过滤波电感L1→电网→滤波电感L2→开关管S6→二极管D1构成回路，电感电流正向续流。市电负半周期工作状态与正半周期工作状态类似。

相较H4拓扑，H6拓扑通过维持共模电压不变，实现抑制共模电流[3]。此外，在H6逆变桥稳定工作时，高频开关管动作时，开关管漏源电压变化ΔVds为1/2Vdc，因此其开关损耗比H4逆变桥开关损耗更小。

2 电流环建模及控制

2.1 H6拓扑电流环的数学模型

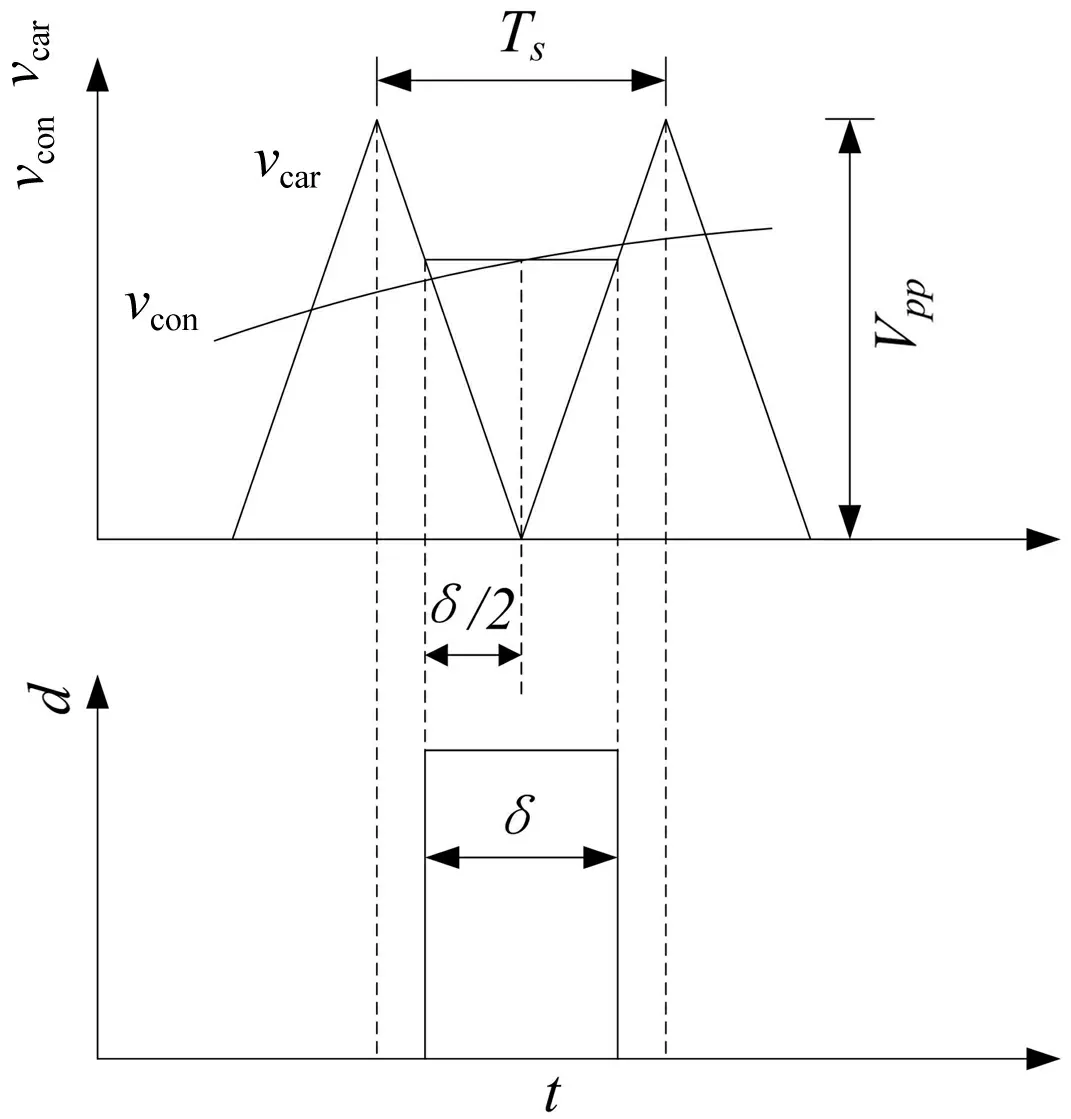
图3 H6拓扑SPWM调制示意图

电流环的控制目的是并网电流跟随电网电压波形，实现单位功率因素并网。由于H6拓扑和H4拓扑的工作原理有较大差别，需要对H6拓扑电流环建模进行深入研究。

在市电正半周期，截取图2的一小部分并放大，得到图3。采用规则采样，δ为脉冲宽度，Ts为开关周期，Vpp为三角载波的峰-峰值。

由图3可得：

(1)

因此可得A臂上开关管S1驱动信号的占空比dA

(2)

类似的，可得在市电负半周期，B臂上开关管S2驱动信号的占空比dB

(3)

设定SA、SB分别为A臂、B臂上开关管的开关函数，开关函数定义为：

(4)

在市电的正半周期，A、B臂上开关管开关函数SA、SB的开关周期平均值分别为：

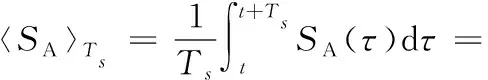
(5)

(6)

类似的，可以得到在市电的负半周期，A、B臂上开关管开关函数SA、SB的开关周期平均值分别为：

〈SA〉Ts=0

(7)

(8)

由式(5)～式(8)可知，无论在市电正半周期还是负半周期，式(9)恒成立。

(9)

逆变桥输出电压VAB为：

VAB=SAVdc-SBVdc

(10)

VAB的开关周期平均值为：

(11)

因此，调制器输入至逆变桥输出的传递函数KPWM为：

(12)

由式(12)可知，H6拓扑的KPWM定义和H4拓扑的KPWM不同。忽略滤波电感上的等效串联电阻和滤波电容电流，可得：

sLIg=KPWMVcon-Vg

(13)

式中:L=L1+L2

由此，可得电流环控制框图，如图4所示。

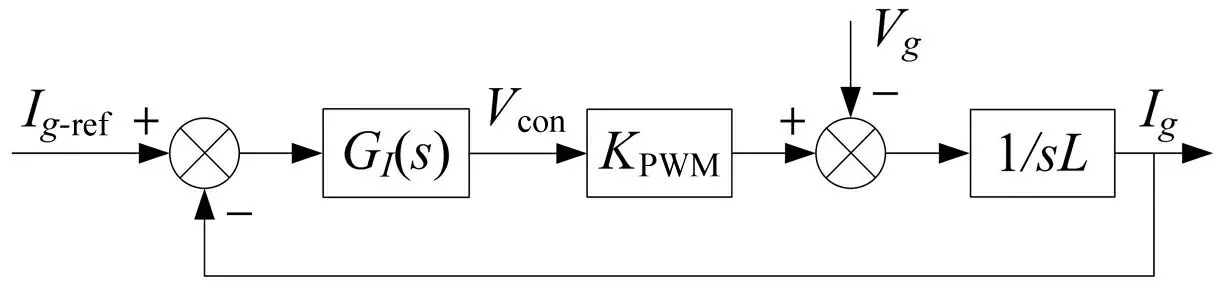
图4 电流环控制框图

2.2 电流环控制策略分析

由于PI控制器在工频处增益为有限值，无法对正弦参考信号无稳态误差跟踪，PI控制产生的稳态误差(主要是相位误差)会影响逆变器的功率因数[4]。此外，并网电流受到电网电压干扰，虽然可以采用前馈控制减小电网电压对电流环的干扰，但在实际应用中，由于电网参数变化等，不能完全补偿电网扰动。为了解决以上问题，可采用PR控制器，PR控制器的传递函数为：

(14)

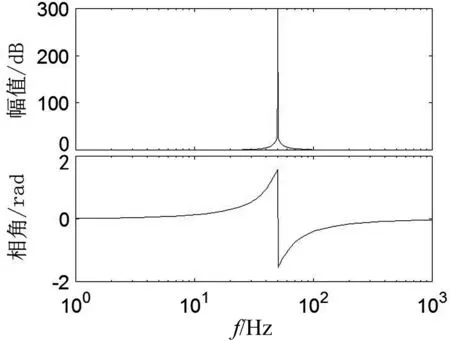
图5 PR控制器伯德图

式中：kp为比例系数;kr为谐振积分系数;ω0为谐振频率。当kp=1，kr=100，ω0=100π时，PR控制器的伯德图如图5所示。该控制器在谐振频率50 Hz处有无限大增益，而在其他频率处增益较小，且主要由kp决定。但在实际应用中，由于模拟系统及数字系统精度限制，PR控制器不易实现。此外，当电网频率发生波动时，PR控制器在该频率处的增益急剧减小，导致并网电流稳态误差增大。

针对PR控制器频率鲁棒性较弱的问题，可利用高增益低通滤波器改进PR控制器[5]817，得到准PR控制器，准PR控制器既保留了PR控制在基波频率处的高增益，还减小了电网频率波动对控制器的影响。其传递函数为：

(15)

图6 准PR控制器伯德图

式中：kp为比例系数;kr为谐振积分系数;ωc为截止频率;ω0为谐振频率。当kp=1，kr=100，ωc=2，ω0=100π时，准PR控制器的伯德图如图6所示。由图6可知，相比PR控制器，准PR控制器在谐振频率处的增益减小，但其带宽增大，降低了对电网频率波动的敏感度。

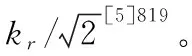
(2)比例系数影响控制器的比例增益。由于谐振控制器对谐振频率处的频率特性有影响，而在其他频率处影响较小，因此，在设计比例系数时，可以先不考虑谐振控制器，按照比例控制设计，然后再设计谐振积分系数[6]。当选用比例控制器时，由图4可知，电流环的开环传递函数为：

(16)

取剪切频率fc=1/10fs，由|G(jωc)|=1，得kp=0.17。

(3)谐振积分系数起到减小稳态误差的作用，在不明显改变剪切频率和相位裕量较大的前提下，应尽可能增大谐振积分系数。以本次研究对象为例，逐渐增大谐振积分系数kr，当kr为10时，剪切频率为开关频率的十分之一，且相位余量较大。

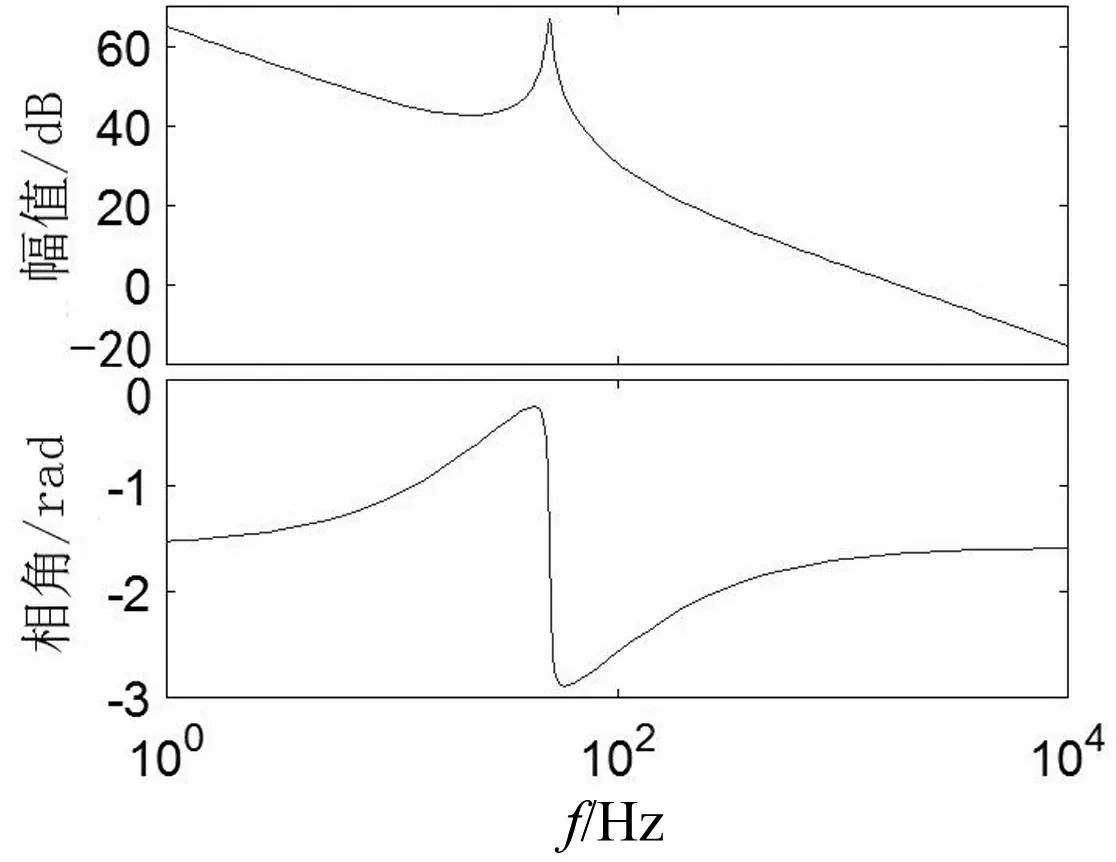
图7 准PR控制系统开环伯德图

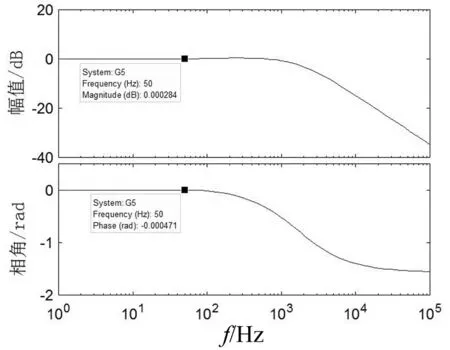
图8 准PR控制系统闭环伯德图

当kp=0.17，kr=10，ωc=2π，ω0=100π时，电流环开环传递函数的伯德图如图7所示。由图7可知，开环系统在50 Hz处增益为66.6 dB，剪切频率为1.8 kHz，相位余量为1.5 rad。

电流环闭环传递函数的伯德图如图8所示。由图8可知，闭环系统在50 Hz处的增益为 0.000 284 dB，相位为-0.000 471 rad，且闭环系统在基波频率附近的增益和相位变化不大，对电网频率波动敏感度较低。

3 电压环建模及控制

3.1 H6拓扑电压环的数学模型

电压环的控制目的是稳定直流母线电压，其建模过程如下。

逆变器双环控制框图如图9所示。

图9 逆变器双环控制框图

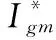
在设计电压环控制器参数时，由于电流环带宽比电压环带宽大得多，可以将电流环简化为一个比例环节。由图9可知，

(17)

如图1所示，在逆变器稳定工作时，忽略逆变器损耗，直流母线侧的输入功率等于交流侧输出功率，即:

VdcIdc=VsIs

(18)

式中：Vdc为直流母线电压；Idc为逆变桥输入电流；Vs为电网电压有效值。

又由图1可知：

Ic=Ip-Idc

(19)

(20)

式中：Ic为直流母线电容电流;Ip为前级升压部分输出电流。

由式(17)～式(20)，可得：

(21)

因此，可以得到电压环的控制框图，如图10所示。

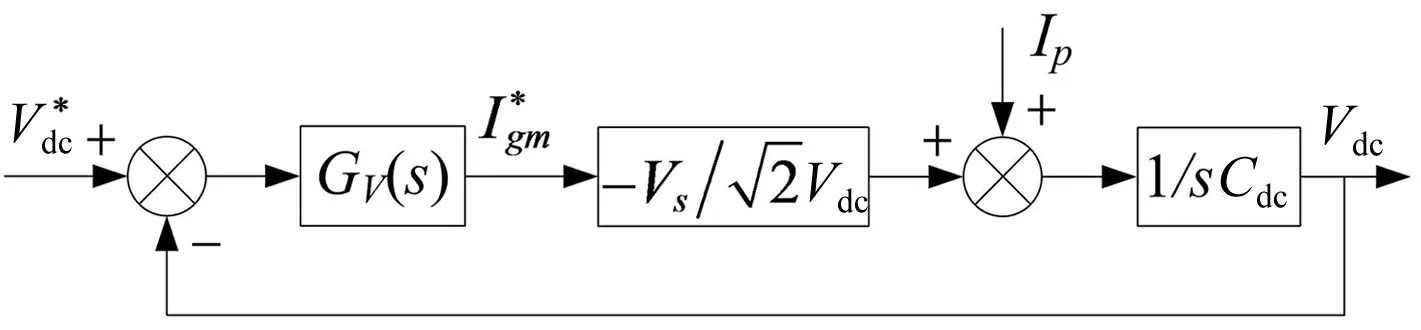
图10 电压环控制框图

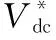
3.2 电压环控制策略分析

逆变器交流侧输出功率为：

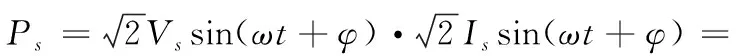
(22)

输出功率除了直流项外，还含有二次谐波项，此二次谐波项造成直流母线电压出现二次纹波，由图9可知，电压环偏差值也含有二次纹波，进而导致电压环调节器输出含有二次纹波，电压环调节器输出乘以单位正弦信号作为电流环的参考输入信号，那么电流环的参考输入信号中就会含有三次谐波。这个三次谐波是电流环的调节器如何设计都去不掉的，因为它在给定的参考信号里。

为了解决并网电流中三次谐波较大的问题，电压环控制器采用type II补偿器(即带有低通滤波器的PI调节器)，同时在电压环中引入陷波器，单独滤除二次纹波。

1)type II补偿器设计

type II补偿器的传递函数为：

(23)

由图10可知，电压环开环传递函数为：

(24)

取剪切频率fc=20 Hz，z=30 rad/s，p=180 rad/s

由|G(jωc)|=1 ，得k1=156.8。

2)陷波器设计

陷波器BSF的传递函数为：

(25)

式中:ω0=2πf0;B=2πfb;f0为陷波器的中心频率;fb为陷波器的带宽。

由之前分析可知，k2=1，f0=100 Hz，ω0=200π rad/s。

取品质因数Q=5，则fb=20 Hz，B=40π rad/s。

4 仿真分析

为了验证准PR控制能够实现并网电流的无稳态误差控制及陷波器能抑制并网电流中的三次谐波，本文搭建了H6拓扑单相并网逆变器的PSIM仿真模型。

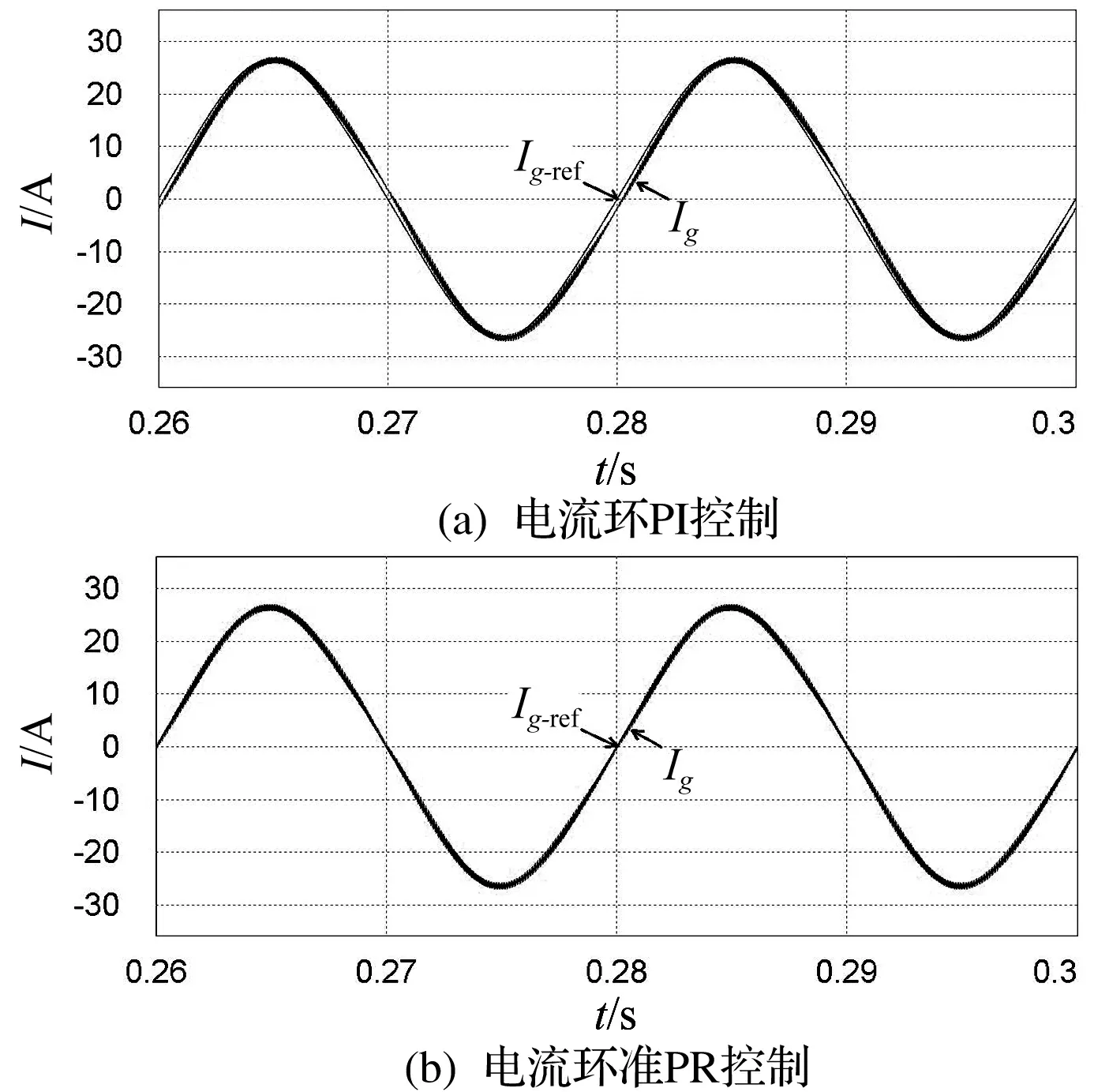
图11 并网电流仿真波形

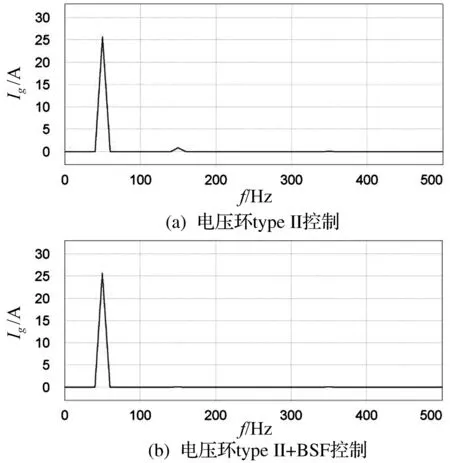
图12 并网电流FFT分析

当电压环均采用type II补偿器，电流环分别采用PI控制器和准PR控制器时，并网电流仿真结果如图11所示。

由图11可知，电流环采用PI控制时，并网电流和给定电流之间存在一定相位差，稳态误差较大；而采用准PR控制时，并网电流和给定电流基本重合，稳态误差较小。

当电压环采用type II补偿器，电流环采用准PR控制器时，并网电流THD为4.01%，其FFT分析如图12(a)所示。由图12(a)可知，电压环仅采用type II补偿器时，并网电流三次谐波分量为0.836 9 A，并网电流的三次谐波较大，导致其THD较大。

当电压环采用type II补偿器和陷波器，电流环采用准PR控制时，并网电流THD为2.35%，其FFT分析如图12(b)所示。由图12(b)可知，并网电流三次谐波分量为0.071 4 A，在电压环引入陷波器后，并网电流的三次谐波很小，THD大幅减小。

5 结束语

本文在分析了H6拓扑工作原理的基础上，建立了其电流环模型及电压环模型。对电流内环控制提出了一种准比例谐振控制，实现并网电流零稳态误差跟踪，提高抗电网干扰的能力，并给出了参数设计的方法。在电压外环控制中，引入陷波器，有效抑制了并网电流中的三次谐波。仿真结果表明，所设计的准PR控制器和陷波器能减小稳态误差和THD。