不同温度状态下啮合异向双螺杆挤出机的流道分布规律
2018-12-12王少峰张媛刘美莲黄志刚赵玉莲古劲宋
王少峰张 媛刘美莲黄志刚赵玉莲古 劲宋 宇
WANG Shao-feng1,2 ZHANG Yuan1,2 LIU Mei-lian1,2 HUANG Zhi-gang1,2 ZHAO Yu-lian1,2 GU Jin1,2 SONG Yu1,2
(1. 北京工商大学材料与机械工程学院,北京 100048;2. 塑料卫生与安全质量评价技术北京市重点实验室,北京 100048)
(1. School of Material and Mechanical Engineering, Beijing Technology and Business University, Beijing 100048, China; 2. Plastic Beijing Municipal Key Laboratory of Health and Safety Quality Evaluation Technology, Beijing 100048, China)
作为双螺杆挤出机的另一大类,啮合异向双螺杆包括啮合平行异向和啮合锥形异向两大类[1]。啮合异向双螺杆由于特殊的构型,形成了C型室,物料被封闭在彼此隔开的C型室中,封闭在C型室的物料不随螺杆作转动,只沿螺杆轴线方向作正位移动,故其广泛应用于挤出成型和配料造粒及其他方面[2]。中国挤出机的应用及发展相对发达国家滞后,自20世纪中叶开始,中国对双螺杆挤出机高分子加工与仿真的研究进展显著,许多模拟与试验的成果被刊登出来,与啮合同向双螺杆研究成果相比,啮合异向双螺杆研究成果却很少[3]。刘湘河等[4]对异向双螺杆S型元件混炼效果的数值进行了研究,证明了啮合方式能影响元件的输送能力、以剪切为主的分散混合能力和分布混合能力,但是其假设流道内熔体作三维等温稳态流动,忽略了温度变化对数值模拟的影响,使得倍数关系不够精确。
目前对于啮合异向双螺杆模拟研究,多数假设其为等温流场[5],而非等温流场问题与啮合异向双螺杆挤出机实际工作状态密切相关,在数值模拟研究中添加非等温流场会更符合异向双螺杆实际工作状态,这样计算问题的非线性更强,是啮合异向双螺杆重要研究方向。本研究拟对啮合异向双螺杆挤出过程进行数值模拟,在等温流动与非等温流动问题下,以双螺杆转速为工艺条件,数值求解模拟过程中压力场、黏度场、剪切速率场以及温度场,分析讨论两种不同温度状态下的流道分布规律,为进一步优化工艺参数提供理论依据。
1 模拟过程
1.1 几何模型的建立
对异向双螺杆模型的设定如下,坐标原点为左螺杆的中心点,X轴方向向右,Y轴方向向上,Z轴方向由右手法则确定,同时其方向与挤出方向相同。为保证计算结果的正确性,模型采用了国际单位制MKS,异向双螺杆的长度单位为米(m),质量单位为千克(kg),时间单位为秒(s),其中左螺杆顺时针转动,右螺杆逆时针转动,根据双螺杆几何学建立图1所示异向双螺杆三维模型[6-9]。螺杆建模参数:螺杆中心距18 mm、螺纹元件导程24 mm、螺纹元件长度24 mm、螺杆外径22 mm。

图1 异向双螺杆模型
1.2 数学模型的建立
1.2.1 等温流动问题 在等温流动问题中,考虑到熔体输送的具体条件及聚合物的特性作以下假设[10]:① 熔体为不可压缩的流体;② 流场为稳定、等温流场;③ 雷诺数较小,层流流动状态;④ 惯性力、重力远不及黏性力,省略不计;⑤ 流道中全布满;⑥ 熔道壁面无滑移;⑦ 流体为非牛顿流体,其本构方程为Bird-Carreau模型。故而,等温流动问题中的连续性方程,动量方程,本构方程可以近似表示为[11]。
(1)
(2)
式中:
u——速度矢量,m/s;
P——流体静压力,Pa;
T——偏应力张量。
流体为非牛顿流体,其本构方程采用Bird-Carreau模型:
(3)
式中:
η0——物料在零剪切应力下的黏度,Pa·s;

n——非牛顿指数;
λc——时间常数,s
1.2.2 非等温流动问题 在非等温流动问题中,物料的黏度与剪切速率和温度有关,使用Bird-Carreau模型来描述物料黏度和剪切速率之间的关系[12]:
(4)
式中:
η0——物料在零剪切应力下的黏度,Pa·s;

n——非牛顿指数;
λc——时间常数,s;
η∞——物料在无穷大剪切应力下的黏度,Pa·s。
另外,在此基础上,使用近似Arrhenius定律来进行黏度的温度修正:
h(T)=exp[-α(T-Tα)]。
(5)
计算中,物料黏度可表示为:

(6)
模拟过程中,计算准确度与物料参数设置相联系,本次仿真模拟中Bird-Carreau本构方程模型参数:在等温流动下物料的本构方程模型参数包括温度190 ℃、零剪切黏度(η0)1 000 Pa·s、松弛时间(λc)1 s、非牛顿指数0.4。在非等温流动下物料的本构方程模型参数包括无穷大剪切黏度(η∞)0 Pa·s、零剪切黏度(η0)1 000 Pa·s、松弛时间(λc) 1 s、非牛顿指数0.4、温度系数0.002 5 ℃-1、物料密度900 kg/m3、导热系数0.207 W/(m·K)。
1.3 边界条件的设定
1.3.1 等温流动问题 速度边界条件:对于螺杆环面上的点,熔体速度V(r)为这个点距离螺杆中心线处的直径距离和螺杆角速度相乘[13],即
ν(r)=Ns·2πr。
(7)
在流道内环面,熔体的速度V(b)是0,即
ν(b)=0,
(8)
式中,
r——在与螺杆轴线垂直的横截面内螺杆外表面到其中心的距离,mm;
Ns——螺杆转速,r/min。
1.3.2 非等温流动问题
(1) 速度边界条件:出口给定法向力和切向力,其中法向力数值采用演变算法,切向力为0;入口法向力和切向力均为0;机筒壁壁面无滑移,法向速度和切向速度均为0。
(2) 热边界条件:在出口和入口这两个面上施加进入流体区域流体温度的边界条件,在该边界条件中,当其速度方向为离开流体区域的方向时,其温度不受限制,而当其速度方向为流入流体区域的方向时,需要给定节点温度[14]。
2 仿真分析
2.1 等温流动问题模拟结果
2.1.1 压力 如图2所示,在螺杆转速为20 r/min时,物料在异向双螺杆的C形小室中正位移向前输送,在螺棱处压力数值变大,熔体产生回流,螺槽处压力数值变小,熔体向前运动。在包含两螺杆轴线的两平面内,压力逐步增大,两啮合螺杆压力值差一个相位。在螺杆转速为10,20 r/min 时,随着螺杆转速的增加,入口截面的压力也逐渐增加。
2.1.2 黏度 如图3所示,在螺杆转速为20 r/min时,同一截面上1处的物料由于左螺杆顺时针转动,经受的螺棱的剪切作用较低,2处的物料还未受到螺棱的剪切作用,与1处相比2处的物料黏度较高,3处由于是左右螺杆啮合区,剪切作用最大,该位置的黏度最低。在螺杆转速为10,20 r/min 时,随着螺杆转速的增加,入口截面的黏度却逐渐降低。

图2 压力云图
2.1.3 剪切速率 如图4所示,在螺杆转速为20 r/min时,左右螺杆啮合区会产生压延间隙,导致漏流,流过其中一螺杆槽底和另一螺杆螺顶之间,由啮合区域上方流向下方,所以左右螺杆啮合区的物料剪切速率大于其他C形区域物料的剪切速率。在螺杆转速为10,20 r/min时,随着螺杆转速的增加,入口截面的剪切速率也逐渐增加。

图3 黏度云图
2.2 非等温流动问题模拟结果
如图5所示,在螺杆转速为10 r/min时,由于物料熔融的主要来源是机筒的热传导,在靠近机筒内表面的物料先受热熔融,温度先升高;在Z方向上,物料由固体—固液两相—液体,温度逐渐升高,所以挤出方向从入口到出口温度呈线性增加的趋势,并且沿着径向向外的方向,温度逐渐增加。为了验证非等温流动问题模拟结果的准确性,在螺杆转速为20 r/min时,观察入口温度云图以及Z方向温度变化云图,结果与螺杆转速为10 r/min的温度变化一致。
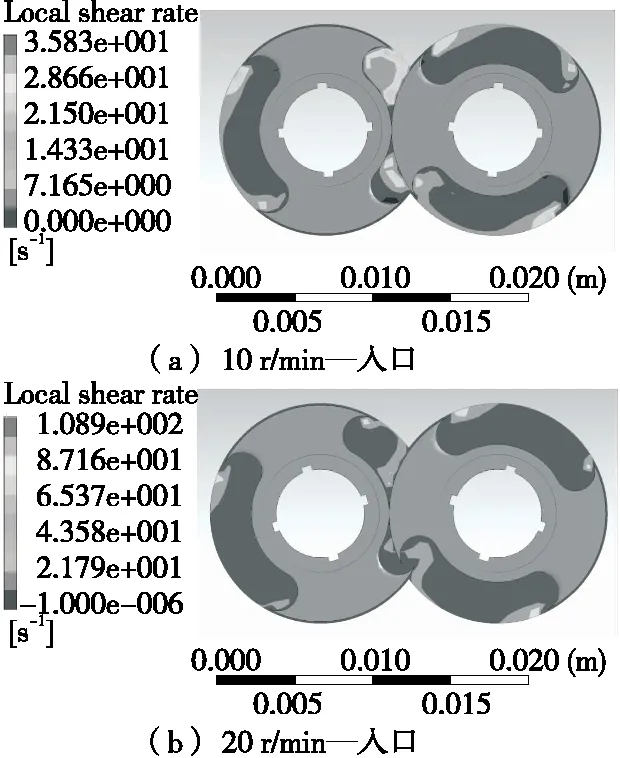
图4 剪切速率云图

图5 温度云图
如图6所示,在螺杆转速为20 r/min时,由于是非等温流动过程,在挤出过程中温度相对于等温过程会升高,相应的压力会增大,黏度会降低。

图6 入口压力云图和黏度云图
3 结论
本研究通过polyflow软件对啮合异向双螺杆挤出等温与非等温问题进行数值分析,得到如下结论:
(1) 非等温过程对啮合异向双螺杆挤出机挤出过程中压力、黏度等物理量的变化存在影响。
(2) 相较于之前研究人员对等温过程中各物理量的分析研究,本研究结果与挤出机实际工作状态更为符合,得出的结论更为准确。
(3) 在挤出机实际工作中,对于转速的要求很严格,本研究未给予最合适挤出机工作的工艺参数,未来可以多次进行模拟与试验,反复对比,以期获得更准确的工艺参数。
