基于能量分析的乘员约束系统优化研究∗
2018-12-12葛如海
葛如海,林 坡,洪 亮
(江苏大学汽车与交通工程学院,镇江 212013)
前言
车身结构、整车约束系统和乘员的伤害之间存在着一定的关系,与车身良好匹配的约束系统不仅能够在极大程度上有效地减小乘员在二次碰撞中所受到的伤害,且可以有效地减缓碰撞过程中乘员的加速度[1]。乘员由于碰撞前具有与车体相同的速度状态,并随着碰撞的过程逐渐降低,最终趋于零,这期间乘员的能量主要通过两种方式进行转移,其中一部分能量是通过乘员与整车约束系统的接触使约束系统发生形变而转移,这部分能量被称为约束能量;另一部分能量是通过约束系统与车身的连接伴____随车身前端部件的形变转移的,这部分能量被称为压溃能量,即ridedown能量[2]。压溃能量与乘员总耗散能量的比值称为ridedown效率。
从时间域的角度考虑,这两个能量转移的过程是同步进行的;但从位移域的角度考虑,这两个能量转移过程可视为彼此独立。针对能量密度或ridedown效率的分析,Mertz等从速度变量的角度进行了能量推导[3],Nancy等从时间变量的角度进行了能量推导[4],Bonello分析了碰撞中能量的转移过程[5]。
本文中从能量的角度提出一种新型的约束系统优化方法,利用MATLAB搭建乘员约束系统的多项式模型进行寻优,旨在简化约束系统的优化历程。
1 能量效率理论
根据文献中提出的能量组合方式和如图1所示[6]的实车正面碰撞试验,结合文献[7]对模型进行进一步推导,建立碰撞车体运动方程解析表达式。
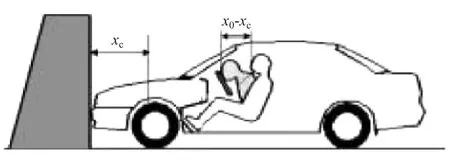
图1 实车正面碰撞
碰撞发生时乘员具有与车体相同的初始速度,乘员的初始动能可近似表示为

式中:m0为乘员质量;v0为乘员初速度。碰撞过程中,若忽略乘员自身发生的形变,则乘员的能量可近似表示为


式中:xc为车体绝对位移;x0c为乘员相对车体位移。则为车体速度,为乘员相对车体速度。
将式(3)代入式(2)可得到
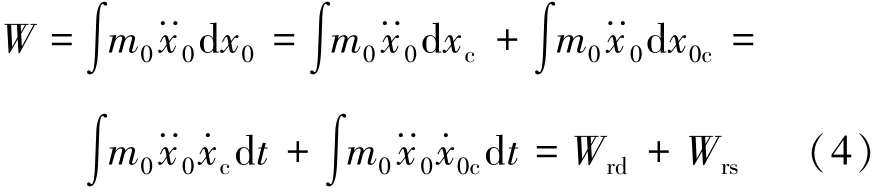
式中:∫m0dt为压溃能量Wrd,即ridedown能量;∫m0dt为约束能量Wrs。与式(4)对应,乘员能量与质量的比值命名为乘员能量密度,即
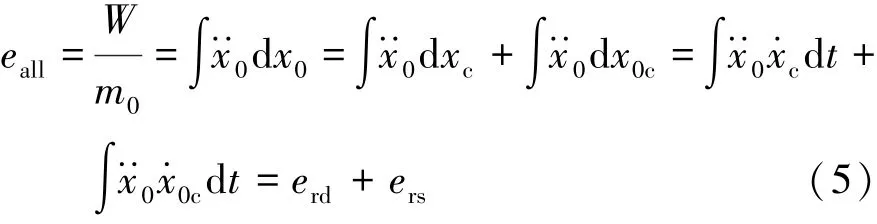
式中:eall为乘员能量密度;erd为乘员压溃能量密度;ers为约束能量密度。另外,车体的ridedown效率定义为乘员压溃能量与乘员初始动能的比值,其表达式为

综上可知:同一工况下,汽车发生碰撞时乘员总能量基本上是一个定值。倘若忽略乘员本身发生形变所产生的能量变化,则压溃能量和约束能量共同吸收了乘员的总能量。因此,在总能量一定的情况下,理论上ridedown效率的高低与乘员受到的伤害大小有直接关系。
2 假人部位划分方法
基于某企业项目搭建MADYMO碰撞仿真模型,该模型与实车碰撞试验进行对标验证,经验证该模型可用于实际系统优化中。而现阶段大部分针对ridedown效率的研究都将假人作为一个整体,以胸部加速度来代替假人加速度,这必然会影响研究的准确性。在参考相关文献[8-11]的基础上,依据2015版中国新车评价规程(C-NCAP)中对假人伤害的评价和对伤害的影响分析,将假人的身体分为3个部分,如图2所示。第1部分是由头部和颈部组成,以头部加速度为分析指标;第2部分是由上肢、胸部和腹部组成,以胸部加速度为分析指标;第3部分是由髋部、腿部和脚部组成,以髋部加速度为分析指标。
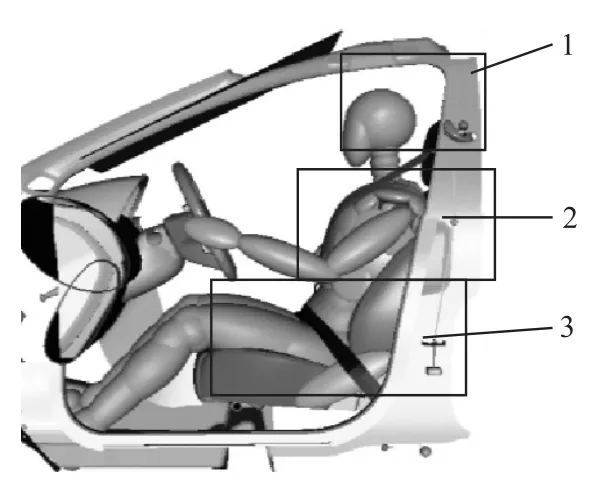
图2 假人各部位划分
3 Simulink能量计算模型的建立
参考上节的理论推导,利用MATLAB/Simulink软件搭建乘员能量ridedown效率计算模型,如图3所示。
图3中的输入数据为假人加速度、初始速度和车体加速度对应于时间的二维数组,最终输出的是假人位移、假人与车辆的相对位移、约束能量密度、压溃能量密度和假人总能量密度,而中间所有的转换和计算过程都由模型完成。
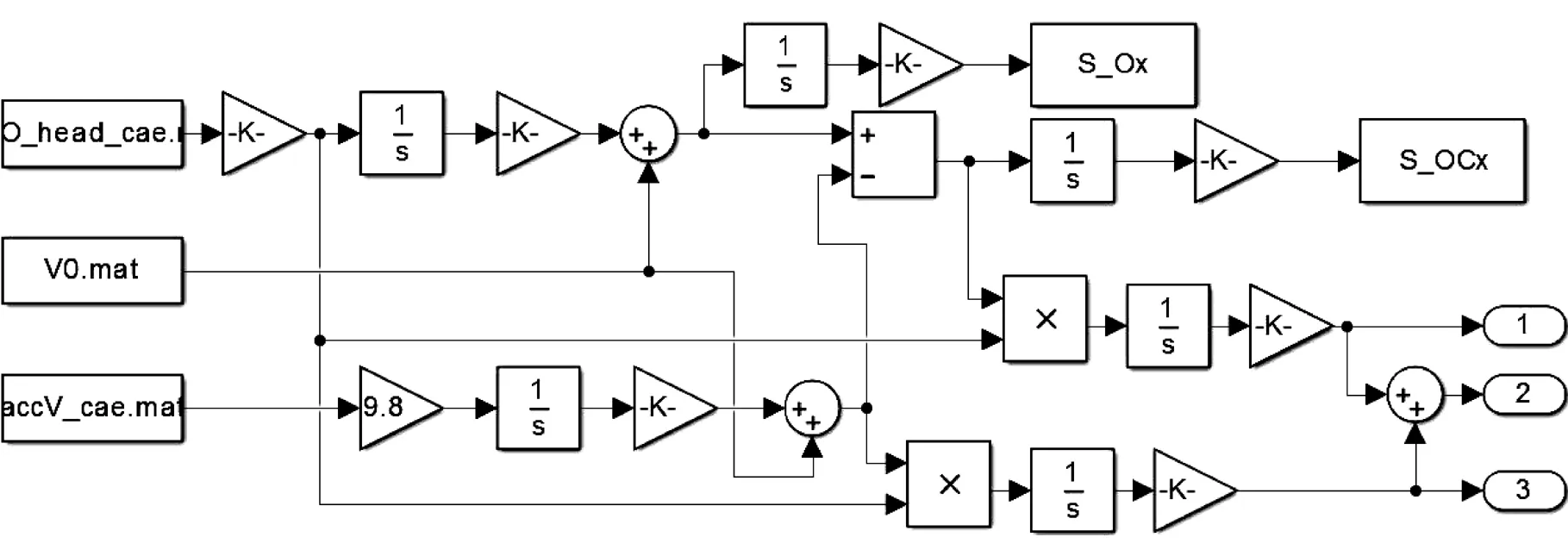
图3 Simulink能量计算模型
将人体分为3个部分,并按图3所示的Simulink模型分别建立计算模型,分别命名为head,chest和lowerbody,如图4所示,最后综合3部分计算能量。
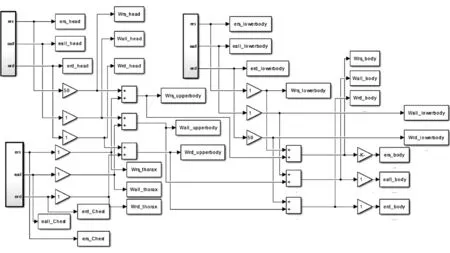
图4 假人各部分能量计算Simulink模型
由图3的数学模型分3部分的输出组成新一轮的输入,再由图4数学模型计算人体3个部位和总体的输出,包括压溃、约束和总能量与能量密度,同时得出ridedown效率。
经验证,所搭建的Simulink能量计算模型精度满足仿真要求,可用于接下来的研究。
4 基于能量分析的乘员约束系统的优化
4.1 约束系统参数与乘员伤害关系的构建
为准确分析假人各部位的能量关系,采用依据某企业项目某款轿车所建立的约束系统模型进行仿真,并与试验进行对标验证,结果如图5~图7所示。
该约束系统模型经过对标验证,仿真与试验曲线基本吻合,证明该模型精度可靠,可作为基础模型进行接下来的研究。
对该模型进行参数灵敏度分析,挑选出3个对系统影响最大的参数,分别是排气孔直径、安全带限力等级和气囊点火时间。利用这3个参数进行三因素三水平的正交试验优化,优化参数水平如表1所示。
进行全正交试验会产生27种搭配组合,利用MATLAB/Simulink软件搭建的能量计算模型对27种组合进行分析计算,分别得出各组合的头部、胸部和髋部ridedown效率,详细数据见表2。
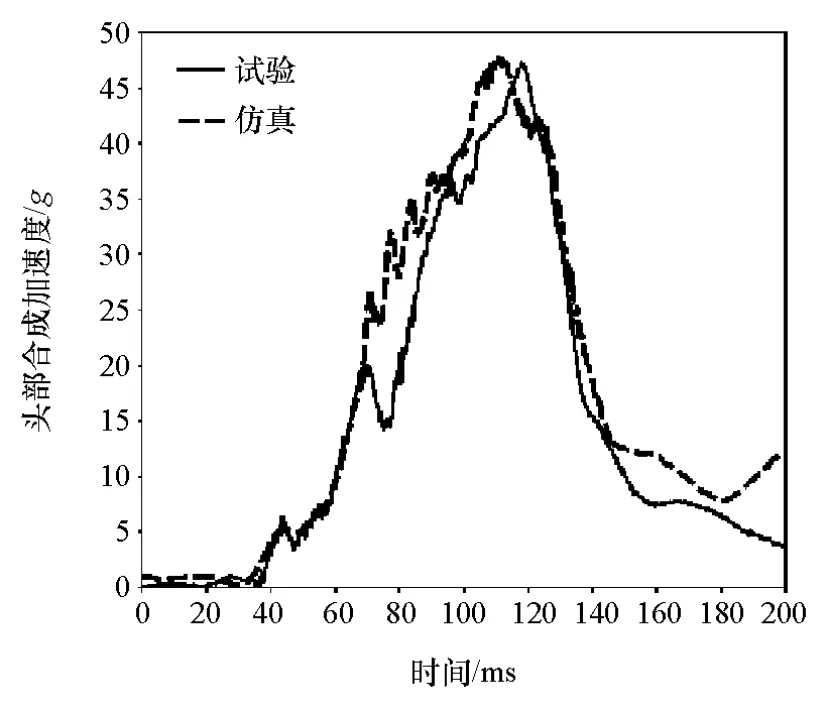
图5 头部合成加速度曲线
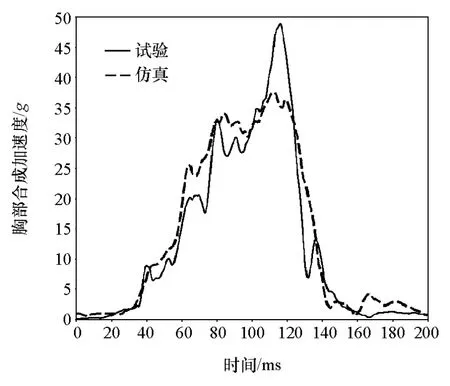
图6 胸部合成加速度曲线
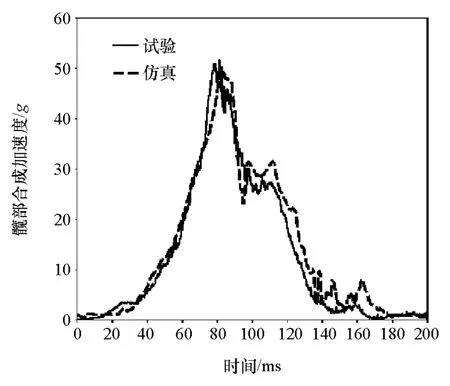
图7 髋部合成加速度曲线
用MATLAB的线性回归拟合功能寻找约束系统参数与乘员各部位ridedown效率和乘员伤害WIC值之间的相关性。
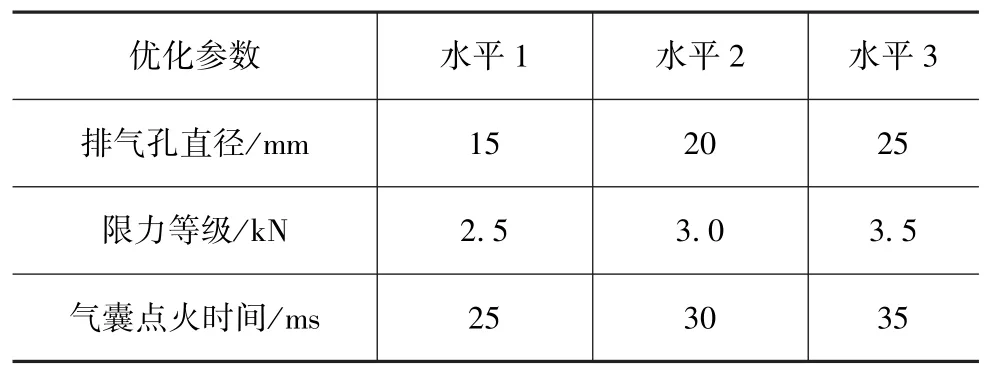
表1 优化参数与水平
将表2中的数据导入MATLAB中进行拟合,获得WIC值与头部ridedown效率、胸部ridedown效率和髋部ridedown效率的关系式,即

式中:μhead为乘员头部 ridedown效率;μchest为乘员胸部ridedown效率;μpelvis为乘员髋部ridedown效率。
将表2中的数据导入MATLAB中进行拟合,可分别获得乘员头部、胸部和髋部的ridedown效率与排气孔直径、安全带限力等级和气囊点火时间之间的关系式,分别为
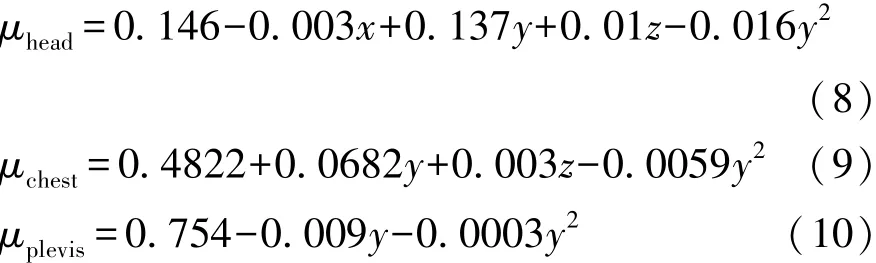
式中:x为排气孔直径,mm;y为安全带限力等级,kN;z为气囊点火时间,ms。
将表2中的数据导入MATLAB中进行拟合,可获得乘员总伤害评价WIC值与排气孔直径、安全带限力等级和气囊点火时间之间的关系式,即
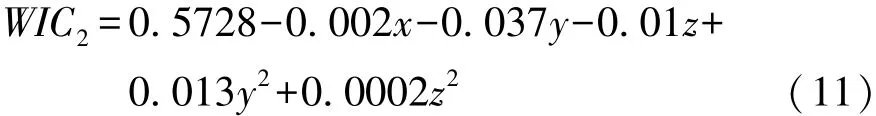
4.2 拟合公式验证与约束系统优化
经MATLAB拟合而成的公式精确性须进行严格的验证,多项式模型的验证和约束系统的参数优化同时进行。详细的参数值与WIC值见表3。
首先,由乘员约束系统参数与WIC值搭建的代理模型WIC2,通过MATLAB软件进行取值范围内的目标函数优化,得到排气孔直径,取30mm,安全带限力等级取2kN,气囊点火时间取25ms时,目标函数WIC2取得极小值为0.365 8。比MADYMO初始模型的WIC值降低了5.62%,乘员约束系统得到了优化,为车内的乘员提供了更优的保护。
接着,分别搭建乘员约束系统参数与头部、胸部和髋部ridedown效率的关系式,将排气孔直径取3 0mm,安全带限力等级取2kN,气囊点火时间取25ms代入关系式中,得出头部 ridedown效率为51.67%,胸部 ridedown效率为67%,髋部 ridedown效率为72.85%。随后搭建乘员3部分的ridedown效率与WIC值的代理模型WIC1,将3个部位的ridedown效率代入代理模型中,得到WIC值为0.368 8。将代理模型WIC1与WIC2的WIC值进行对比发现误差只有0.81%,说明利用MATLAB搭建的约束系统代理模型稳定性很高,完全可以运用到仿真研究中。
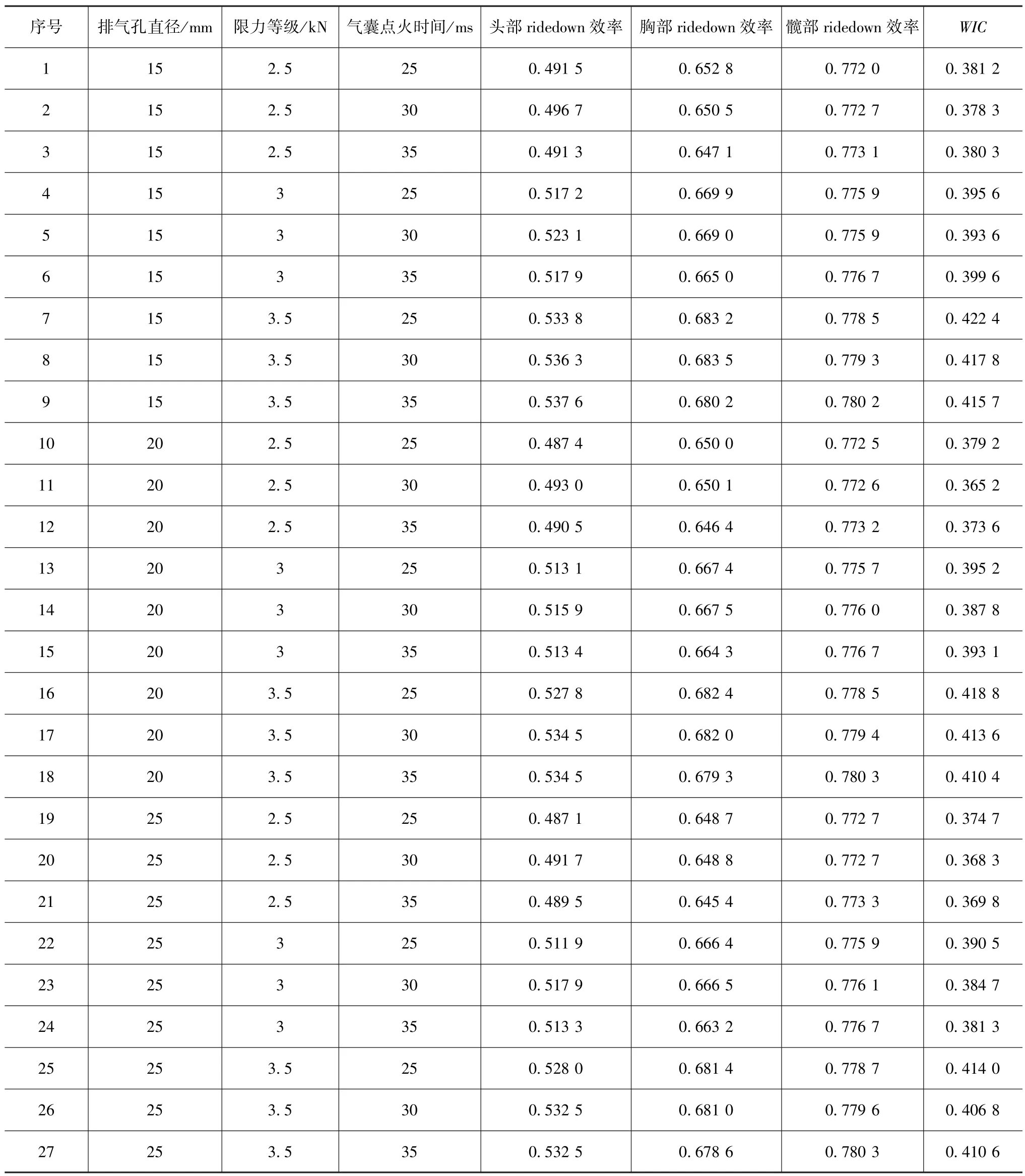
表2 正交试验系统参数与头部ridedown效率
最后,将前面得到的约束系统参数,即排气孔直径30mm、安全带限力等级2kN和气囊点火时间25ms代入MADYMO约束系统仿真模型中进行运算,得出乘员的WIC值为0.367 2。将其与代理模型进行对比发现,代理模型与MADYMO仿真模型之间乘员伤害WIC值之间的误差为0.38%,说明所搭建的代理模型可以代替MADYMO软件进行乘员约束系统参数优化。
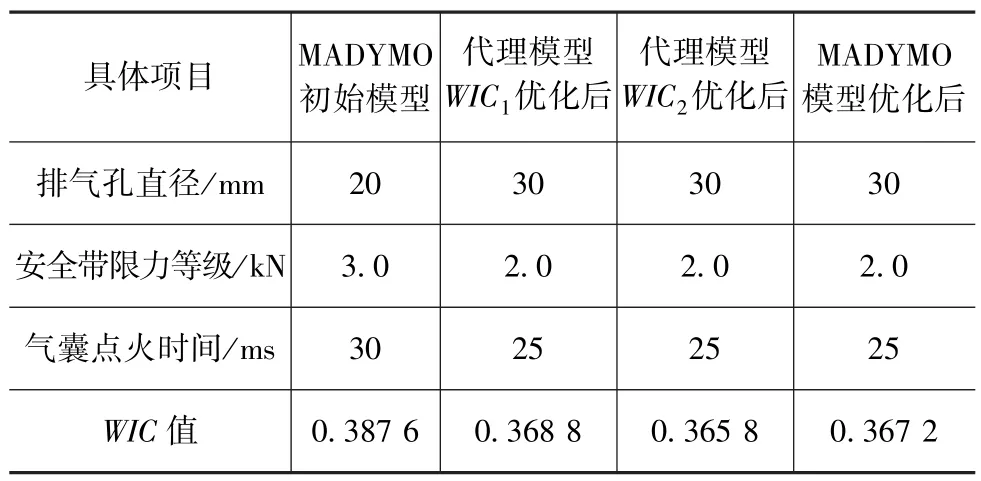
表3 模型优化前后参数取值和WIC值
5 结论
针对汽车正面偏置碰撞中乘员约束系统的保护性能进行了实车试验,对乘员ridedown效率进行研究,利用MATLAB/Simulink软件搭建乘员能量计算模型,并提出一种新型的乘员约束系统优化方法。通过分析比较MATLAB多项式仿真模型与MADYMO仿真模型,证明新型的多项式仿真模型精度较高,可替代MADYMO模型进行约束系统优化,优化后的结果表明乘员的总伤害评价WIC值接近最小值,为0.365 8,与初始模型的0.387 6相比降低了5.62%,乘员约束系统的性能得到了明显的改善。
