汽车空调风道气动噪声仿真方法研究∗

2018-12-12卿宏军

汽车工程 2018年11期

卿宏军，刘杰

(1.湖南大学机械与运载工程学院，长沙 410082； 2.常州湖南大学机械装备研究院，常州 213164)

前言

汽车空调噪声严重影响车内乘坐环境的舒适性，与传统动力汽车相比，电动汽车由于缺少发动机噪声的掩蔽，该问题尤为明显。气动噪声作为空调噪声主要成分，一般由两部分组成:第一部分为鼓风机运转时产生的噪声，通过混合箱、风道和出风口向外辐射传播；第二部分为气流流经各结构时，由于气流通道结构的改变导致气体在其结构内部形成涡流而产生气流再生噪声。大量研究结果表明，风道气流再生噪声是中高频空调噪声的主要来源[1]。因此，在设计阶段基于CAE技术预测其噪声强度可降低开发成本和风险。

2008年，奥迪、宝马、戴姆勒、保时捷和大众等德国整车企业联合发布了一个简化风道模型及其相关的试验结果，并基于有限体积方法和格子玻尔兹曼方法进行数值仿真与验证，但并未开展远场声辐射仿真分析方法研究[2]。随后，Wiart与Geuzaine等人针对该风道采用混合方法求解远场辐射噪声，获得了较好的结果[3]。2011年前后，Lee与Perot等人采用直接模拟方法建立了一套完整的HVAC气动噪声仿真分析和试验验证流程[4]。2015年，Tupake采用直接模拟方法对某款车型HVAC气动噪声声源进行了优化控制[5]。这些研究虽然取得了很大的成功，但因存在计算规模较大且远场辐射噪声仿真精度不高等问题，故较难在系统层面模拟和评估诸多参数对远场(乘员舱人耳附近)噪声水平的影响。

针对空调风道气流再生噪声的仿真方法，尤其是远场辐射噪声的计算问题，为满足工程开发快速响应需求，本文中基于FW-H模型建立一种高效高精度的方法，并与其它3种常见方法和试验结果进行对比，最后将该方法应用于实际工程中。

1 仿真分析方法

对于风道气流再生噪声，Humbad基于大量试验数据拟合建立了一种经验预测方法[6]，该方法计算效率高且结果精度满足工程开发要求，非常适合设计前期进行噪声预测，但因该方法需大量试验样本，故文中不包含该类经验方法，而仅从数值计算角度阐述当前比较热门的仿真分析方法，主要包括声类比法、直接模拟法和联合仿真法(有限元法、边界元法等)，各方法计算流程如图1所示。

1.1 声类比法

声类比法最初由 Lighthill提出，后来 Ffowcs Williams和Hawkings对该方法进行了改进与推广，给出了一个更加通用的FW-H波动方程:

式中:p′为远场测点声压；x-为远场测点距声源的距离；t为时间；p′T，p′L和 p′Q分别为单极子、偶极子和四极子声源在监测点处所产生的声压，其详细计算公式可参看文献[8]。

图1 计算流程图

该方程首次明确了气动声学中3种典型声源，即单极子、偶极子和四极子声源。声类比法一般把气动噪声特征的求解过程分成两个步骤，首先采用CFD手段计算声源处的瞬态流场，获取声源强度及其分布信息，然后选取声源面，最后根据声波辐射传播机理，基于积分方法求解远场接收点处的声波特性。虽然该方法不能预测管道或封闭空间内的内场噪声，但却非常适用于计算自由空间的声传播问题，例如汽车、火车和飞机等运载工具的外部气动噪声问题。

该方法只需在一个软件中独立完成，计算过程相对简单，应用较广，其计算精度主要与声源计算精度和声源面选择有关。声源面示意图如图2所示，在本文中，以出风口射流周围可穿透包围面为声源面的方法命名为方法1，而以风道与风门固体壁面为声源面的方法命名为方法2，并将在声源计算精度相同的条件下，对比研究声源面选择对远场辐射点声压计算精度的影响。

图2 声源面示意图

1.2 直接模拟法

直接模拟法是一种能同时求解非定常流动产生的声源和声辐射特征的数值方法，它能准确捕捉波的传播特征。虽然具有较高的精度，但由于要求具有高精度的无反射边界条件与高分辨率的数值离散格式，且为了减少数值色散对物理声波的影响，还要求近场与远场的网格尺寸保持一致性，因此，求解规模较大，对计算硬件资源要求较高，目前仅广泛应用于求解近场气动声学问题，如风振噪声、后视镜近场气动噪声等。本文中的直接模拟方法将采用StarCCM+软件中的SST k-ω DES模型、H-BCD空间离散格式和2阶时间离散格式同时求解近场和远场声问题，命名为方法3。根据文献[7]中的色散关系分析方法，获得了常用空间离散格式的色散和耗散特性，分别如图3和图4所示。从图中可以看出，虽然2阶中心差分格式具有较好的色散和耗散性能，但由于其耗散值为零，容易引起计算不稳定等问题。

图3 典型格式的色散

图4 典型格式的耗散

1.3 联合仿真法

联合仿真法通常是指几种CAE软件联合求解气动声特征的数值模拟方法，一般先采用CFD技术瞬态求解关键区域的脉动压力信息，然后将获得的脉动压力信息插值转换成频谱信息，再将频域信息作为边界元、无限元、有限元或统计能量分析模型的边界条件，最后采用这些软件求解声场获得其相关物理特征。CFD结果的精度是联合仿真法可靠性的基础，因此将采用直接模拟法中的数值算法获取脉动压力，采用有限元法求解远场声场，该方法被命名为方法4。

2 仿真模型与试验

为验证上述分析方法的精度，本节将采用文献中公布的模型进行分析，并与试验结果进行对比。该模型由德国几个主要汽车企业共同发布，旨在通过该简化模型的试验结果来验证空调HVAC风道噪声的仿真方法，最终获得一种可信的仿真方法。因此，该模型可用于本文中仿真方法的对标验证。

2.1 模型与试验装置

为体现空调风道的基本特征，该标准风道模型由一段90°弯折的方形管道和简化风门组成，如图5所示。风道来风由鼓风机提供，入口平均来流速度约为7.5m/s。该模型相对简单，在该风速下由风道引起的气动噪声强度相对较低，因此，须降低测量系统背景噪声对测量结果的影响。

图5 风道模型

试验装置示意图如图6所示，将鼓风机置于混响室，将测试风道置于全消声室，当气流流经鼓风机后通过两级消声器消除鼓风机背景噪声，然后通过转弯接头调节湍流强度，进入湍流完全发展的平顺管道，最终从测试风道排出。为观察风道内的时均流场分布，采用PIV测量系统对截面Y＝0的流场情况进行测量，且在风道出口段布置7个嵌入式传声器，用以采集非定常压力脉动信息；此外，为测量远场辐射噪声强度，在距出风口截面形心1m的球面上，布置289(17×17)个传声器。PIV测量系统、壁面压力脉动采集传感器布置位置和远场点分别如图7所示。

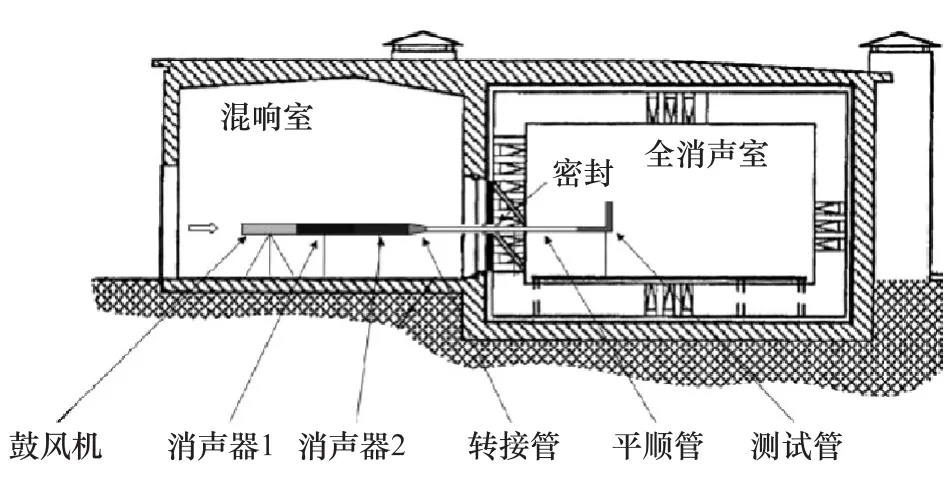
图6 试验装置示意图

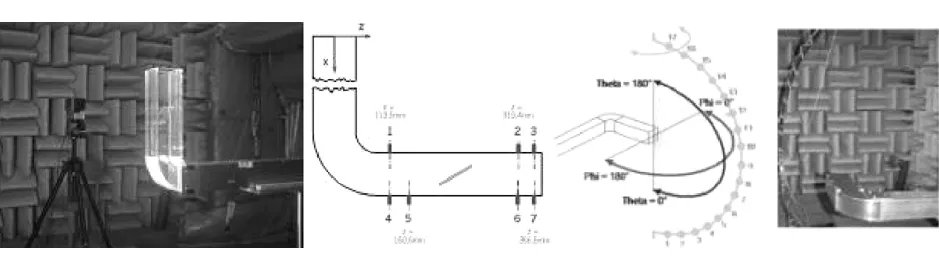
图7 PIV测量系统与测点

2.2 仿真模型

为减小边界条件对计算结果的影响，最大限度保持与试验条件的一致性，计算风道前段延长一段3m长的等截面管道，计算风道出口处连接一个稳压腔。风道内部网格尺寸为2mm，为捕捉风门处的涡流特征，该处网格尺寸加密为1mm，为获得更多流场细节，风道出口喷流区增加4层加密盒，网格尺寸依次为2，4，8和16mm。受流体黏性影响，管道内壁面区会形成附面层，本文中在近壁面区采用了6层精细棱柱网格来计算附面层的影响，整个计算网格共计3 000万。具体计算边界条件如下:进口边界为速度入口，速度为7.5m/s，出口边界条件为压力出口，其余边界条件为固体壁面边界。

稳态计算采用RNG湍流模型进行求解，当稳态计算稳定后，将稳态计算结果作为瞬态计算的初始值，在瞬态计算开始时，按照2.1节中的方法分别设置好声源面与数据采集监测点，并输出脉动压力数据。瞬态求解的总时间设定为0.6s，由于瞬态流场从启动到相对稳定需要一个过程，因此0.1s时才开始记录。由于本文中感兴趣的频率区间为200-2 000Hz，本次计算的最高频率设定为2 500Hz，根据奈奎斯特采样定律并考虑计算时间成本，取样频率取为5 000Hz，即对应的时间步长为0.2ms。

3 结果分析与验证

针对各阶段获得的仿真结果，本节将从稳态流场结果、近场声压级和远场声压级3方面对其进行试验结果对比分析。

3.1 稳态结果

管道内Y＝0截面上X方向和Z方向的时均速度场分别如图8与图9所示，从图中可以看出，在拐角处内端面区域存在一个气流滞留区，该处存在明显涡流，在风门尾流区存在两个较大旋涡，根据涡声理论，这些涡流均是引起气动噪声的主要原因。虽然仿真结果较好地体现了这些涡流特征，且与PIV试验结果吻合程度较高，但由于来流边界层厚度的差异及边界层数值模型、湍流模型与网格尺寸的影响，拐角处剪切层的分离脱落区存在差异。

图8 在Y＝0截面上X向时均速度分布

图9 在Y＝0截面上Z向时均速度分布

3.2 近场声压级

图中监测点1、监测点2和监测点6的声压级仿真值与试验值对比分别如图10、图11和图12所示。由图可见:仿真结果与试验结果吻合较好；脉动压力能量主要集中在200Hz以内的低频区域；监测点1位于拐角处内端面，如3.1节中稳态流场分析结果所示，由于该处剪切层涡流分离脱落区域与试验结果存在差异，导致该处壁面压力脉动频谱与试验值相差较大，在全频段区域，仿真值明显高于试验值，但其趋势基本一致；监测点2和监测点6位于风门涡流区，该处涡流特征仿真值与试验基本一致，因此，这两个监测点的脉动压力频谱曲线与试验值吻合较好。监测点1、监测点2和监测点6脉动压力总声压级仿真相对误差分别为5%，-2.2%和-1.5%。

图11 监测点2声压级仿真值与试验值对比

3.3 远场声压级

气流流经风门并沿+Z方向喷出后，在喷口处形成强烈湍流涡，涡在脱落、卷起、碰撞融合等演进过程中形成气动噪声，并向四周辐射，其噪声源分布如图13所示，该简化风道主要噪声源位于风门后缘和喷口射流中心区，声能量主要集中在低频段。

图12 监测点6声压级仿真值与试验值对比

为了验证新方法的准确性和各方法的优劣，将距离喷口中心点1m的半球上均匀布置37个测点，将37个测点声压级的平均值与试验数据进行对比，如图14所示。由图可见:方法1精度最高，与试验值基本吻合；方法2次之，略高于试验值，频谱曲线基本特征与试验值一致；方法4与试验值频谱曲线趋势基本一致；方法3与试验值相差较大。