基于Copula和多成分GARCH的股市高频波动溢出研究
2018-12-11翟晓婧
翟晓婧 朱 丹
(南昌大学,江西 南昌 330000)
在过去,GARCH模型得到了广泛的扩展。但是,将Copula理论运用于高频数据的研究还不多。大致上,可以将Copula理论运用于高频数据研究的文献分为三类,一类是直接将Copula与边缘模型相结合对多变量高频数据之间的关系进行研究。一类是用高频数据计算出“已实现”波动率等构建边缘分布模型,再与Copula模型结合进行低频数据波动关系的研究。最后一类是将Copula和ACD模型结合运用于超高频数据。考虑到高频数据的日历效应特征并结合SJC-Copula为建模工具对金融市场尾部波动溢出进行的研究还未出现,本文的研究有助于填补这一空白。
一、模型和研究方法
(一)多成分GARCH模型的基本理论
本文把采集高频收益率样本的天数依次标记为t(t=1,…,T)。在每天里收集N个收益率样本,每天的高频样本依次标记为i(i=1,…,N)。可以构造出多成分GARCH模型的基本形式:

在上式 (1)里,rt,i表示第t天第i个对数高频收益率数据,μt,i为rt,i的条件均值,εt,i为残差项。qt,i代表日内标准差成分,σt为第t日收益波动的标准差,si为日历标准差成分,zt,i服从iid(0,1)标准化新息,zt,i服从的分布较常见的有高斯分布、学生t分布等。本文选择使用学生t分布,并设自由度参数为λ。
这里,本文将多成分GARCH模型进一步表示成:

上式(2)中,μ代表均值的常数部分,p为选定的最大滞后阶数。rt,i-j为rt,i的第j个滞后项。
(二)多成分GARCH模型的参数估计
考虑到多成分GARCH模型既利用了低频数据又使用了高频数据,本文使用分步法进行估计:
第一步先估计σt。在对每日收益标准差σt估计时,我们选用GJR-GARCH(1,1)模型进行。
第二步,对日历标准差成分si和多成分GARCH模型的参数等进行估计。估计方程式如下:

在本文里,我们用剔除对数高频收益率条件均值后的残差替换对数高频收益进行估计。估计式变为:

如果我们将(2)式的前两个方程式分别代入(3)式和(4)式,可以发现使用(4)式计算日历标准差成分比(3)式更能明晰表现出日历标准差的估计式与多成分GARCH模型里设定的日历标准差的对应关系。
其后,将第一步估计得到的σˆt和(4)式确定的sˆi的表达式代入(2)式,对多成分GARCH模型用极大似然法进行估计得到参数值和残差序列。在式(2)里,有参数,那么,学生t分布下的对数似然函数可以表示为:
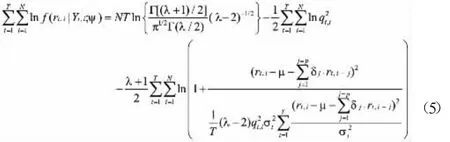
在上式(5)中,Yt,i表示直到t日第i个样本点的信息集合,Γ(·)为Gamma函数,并要求学生t分布的自由度参数λ>2。
(三)SJC-Copula模型的形式及参数估计
Copula理论的发展极大地丰富了多元变量之间相关性研究的内容。尾部相关系数可以用来捕捉当一个预测变量为极值时,另一个观测变量也出现极值的概率。尾部相关系数引申出来的一个概念是条件尾部相关系数。在实证研究中,常用τU(τL)表示条件上(下)尾相关系数。当τU(τL)大于零且小于等于1时,则说明存在上尾(下尾)相关关系,否则就表示不存在这种相关关系。Joe-Clayton Copula函数形式为:

上式中 κ=1/log2(2- τU),γ=-1/log2τL且 τU∈(0,1),τL∈(0,1)。Joe-Clayton Copula不仅能对尾部相关关系进行静态描述,也可以对它们的动态的变化进行刻画。Patton发现Joe-Clayton Copula无法度量出上下尾相关系数相等的情况,提出了SJCCopula。其具体函数形式可表示为:

Patton在定义Joe-Clayton Copula函数中的参数时变性的基础上,得到了时变条件上下尾相关系数的表达式。

其中的Λ(·)表示的是logistic转换函数,其表示形式为Λ(x)=(e-x+1)-1,这一变换有助于保证上下尾相关系数永远处于(0,1)范围内。
在对SJC-Copula进行估计时,本文运用基于核密度的极大似然法(MLK)来实现。在运用MLK法进行Copula参数估计时,需要分两步进行。
第一步,利用核平滑分布估计函数将标准残差xnt转换为均匀变量unt;

其中,hnT为窗宽,kT(·)为核函数,一般取Gaussian核函数。
第二步,估计c(·)的待估参数向量θ:

二、实证研究
(一)实证样本数据选取及其统计特征描述
多成分GARCH模型既用到了低频数据也用到了高频数据,本文低频数据来源于Wind数据库,高频数据来源于锐思高频数据库,结合本文的需要对数据进行处理,分别计算出每日和每10分的对数收益率:

Rt,Pt分别表示第t个交易日的收益率和收盘价格;rt,i,Pt,i表示第t个交易日第i个收益率和收盘价格。另外,本文规定,当i=1时pt,i-1取上一日最后采集的收盘价格。对四个行业指数10分钟高频数据样本分别进行统计特征分析,发现呈现出明显的尖峰厚尾性。同时它们也表现出显著的左偏特征。四个样本都显然不服从正态分布,而且除地产指数(DCZS)外,其它三个指数都不能拒绝存在序列自相关性的假设。
(二)边缘分布模型的参数估计及检验
通过使用Ljung-Box-Q检验和Kolmogorov-Smirnov检验变换后的序列,发现这4个时间序列服从iid(0,1)的均匀分布。这表明,多成分GARCH模型能够较好地拟合边缘分布,可以用它进行四个指数高频收益率序列的建模。
(三)时变SJC-Copula模型的参数估计及检验
依据SJC-Copula模型的理论,将得到的概率积分变换后数据代入SJC-Copula模型估计参数,得到静态SJC-Copula模型的上下尾相关参数以及时变SJC-Copula模型(8)和(9)式中参数,并计算出AIC的值。
(四)上海股市行业板块高频风险传染实证结果分析
1.下尾相依性分析。只有在地产指数与其它行业指数之间存在时变的高频下尾相依性,而在其它指数之间则不存在时变的下尾相依性。从波动幅度可以看出,地产板块与商业板块之间的下尾相依性波动较大,地产板块与工业板块、公用事业板块的下尾相依性波动幅度则较小。
2.上尾相依性分析。只有在地产指数与其它行业指数之间存在时变的高频上尾相依性,而在其它指数之间则不存在时变的上尾相依性。从变动幅度可以看出,地产板块与商业板块之间的上尾相依性变动较小,地产板块与工业板块、公用事业板块的下尾相依性波动幅度却较大,这点与下尾相依性表现的正好相反。同时,下尾相依性比上尾相依性更大,而且在表现出时变上下尾相依性特点的地产指数与其它板块之间相依性的波动也呈现出明显的不对称特点。
本文使用能够同时描述静态和动态上下尾相依性的SJC-Copula和适用于高频数据的多成分GARCH模型分析了上海股市行业板块之间的风险溢出关系。研究发现工业指数、商业指数和公用事业指数之间有较强的上下尾相依性,且这种相依性呈现出较为恒定的状态。但在地产指数与其它指数之间,则呈现出相对较弱的时变上下尾相依性。
