开口式正方形刚性索穹顶的性能与灵敏度分析

岑迪钦 庄 宁

(1.浙江大学建筑设计研究院有限公司，浙江 杭州 310028；2.杭州启迪协信丁桥赵家科技发展有限公司，浙江 杭州 310028)

0 引言

索穹顶结构是一种受力合理、结构效率和经济效率高的新型大跨度预张拉结构，主要起源于Fuller[1]的张拉整体结构的思想。其中，美国著名结构工程师Geiger第一次把该中结构类型应用于汉城奥运会的体操馆和击剑馆[2]，获得了较大的成功。此后这类工程得到了广泛的应用，其中又以Levy等[3]设计的亚特兰大体育馆的乔治亚穹顶、美国伊利诺斯州大学的红鸟体育馆、佛罗里达州的太阳海岸穹顶、圣彼得堡的雷声穹顶等最具代表性。这些工程说明了索穹顶结构强大的生命力和广阔的工程应用前景。

文献[4]～[7]提出了一些新的索穹顶结构形式，但依然没有解决索穹顶结构中存在的问题，比如结构的脊索容易退出工作、结构设计精度要求高、结构施工技术要求高等问题。为了较好地解决和避免这些问题，文章在文献[8]的基础上，提出了一种以刚性杆件代替结构脊索的开口式正方形索穹顶结构，并采用Ansys软件对其进行了结构的性能分析和结构随机变量的灵敏度分析[9]。

1 开口式正方形刚性索穹顶结构模型

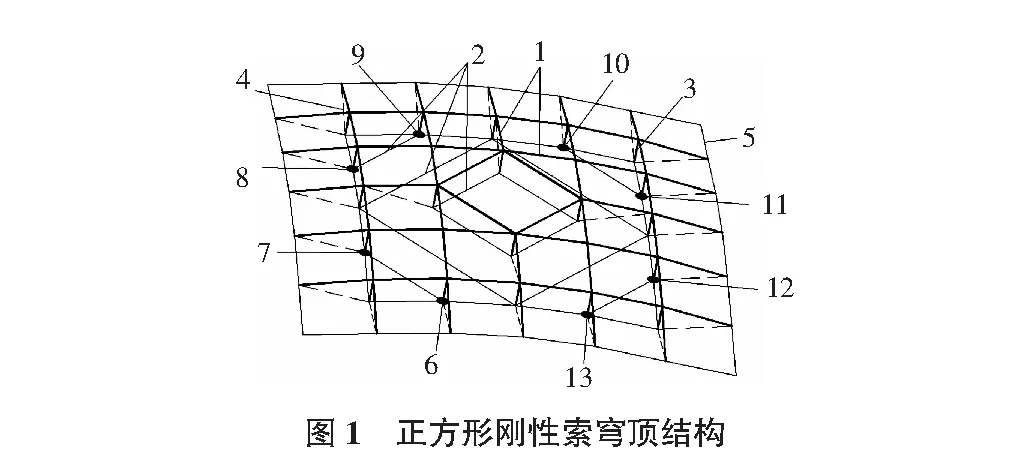
图1是开口式正方形刚性索穹顶结构的一种计算模型，其中，编号1～编号5分别为代替原脊索的上弦刚性杆件，下弦拉索，竖直撑杆，斜索以及边上环梁。刚性杆件按相互垂直的网格布置在一个上凸的双曲面上，结构周边设有边环梁。

计算模型中的竖直撑杆设置在对称轴上的网格节点及周边网格节点，斜索连接于对称轴上的网格节点、环梁与刚性杆件的节点与内侧相邻竖直撑杆下端之间，对称轴上的竖直撑杆下端连成一个封闭的正方形的下弦拉索环，周边的竖直撑杆下端相邻节点之间用下弦拉索连接，同时，在节点6和7，8和9，10和11以及12和13之间也用下弦拉索进行连接。

2 结构性能

对图2所示的计算结构模型进行性能分析，其中，结构跨度为48 m，结构矢高为3 m，承受满跨均布荷载P作用。计算结构模型中的索截面面积取值为14.33 cm2，刚性杆件截面面积取值为43.23 cm2，拉索的弹性模量取值为1.85e11Pa，刚性杆件的弹性模量取值为2.06e11Pa。竖直撑杆高度取值均为3 m，截面面积取值均为48.70 cm2。结构计算的初始条件为在拉索预应力的作用下，结构最大初始位移控制在L/800，L为结构计算跨度。节点位移ω的计算结果如图3所示。

从图3可以看出，在满跨均布荷载作用下，在初始时刻，结构存在一定的向上的初始位移，其节点位移的变化大致上呈线性，节点位移变化较为均匀，且最大位移较小。

3 结构的灵敏度分析

对图2计算结构模型进行双随机下的可靠性灵敏度分析。分析的方法为常用的灵敏度分析方法——Monte Carlo方法。

随机变量的选取为结构竖杆、刚性杆件和拉索的弹性模量Esg，Egg，Els，结构竖杆、刚性杆件和拉索的密度Rousg，Rougg，Rouls，结构竖杆、刚性杆件和拉索的截面面积Asg，Agg，Als，均布荷载Load以及斜索XS3的预应力水平PP。表1为以上随机变量的统计参数。

计算模型的位移限值取为L/200，其中，L为结构的跨度。选取位移控制下的失效模式对结构进行计算分析，分析得到的随机变量的灵敏度结果如图4所示，其中，浅灰色表示刚性杆件截面面积Agg，灰色表示刚性杆件弹性模量Egg，黑色表示均布荷载Load。计算过程中考虑结构自重影响。

表1 随机变量的统计参数

由图4可以看出，在位移控制下，随机输入变量中的刚性杆件截面面积Agg、刚性杆件弹性模量Egg和均布荷载Load对结构失效较为敏感，其灵敏度分别为80.8%，40.1%和38.9%。

4 结语

1)开口式正方形刚性索穹顶结构平面可根据需要灵活布置，可应用于各种不同的实际工程项目。2)在荷载作用下，开口式正方形刚性索穹顶结构的节点位移变化较为均匀，整个曲面形状较为平稳。3)在位移控制下，较为敏感的变量为刚性杆件截面面积、刚性杆件弹性模量及均布荷载。4)采用Monte Carlo方法能较好地进行随机灵敏度分析。