连续梁拱组合结构风致抖振响应分析

余 海 洪

(中铁四川生态城投资有限公司，四川 眉山 620500)

1 概述

连续梁拱组合结构是两种形式的连续梁桥和拱组合。连续梁拱桥包含两种结构的特征，具有结构刚度大，跨越能力强，动力性能好，外形美观，施工方便等优点。近年来，这种类型的桥梁已经逐渐发展为超轻，大跨度，由风引起的抖振问题日益突出。

桥梁抖振是由湍流中的脉动组件引起的一种强迫振动。频域分析方法是热门的分析方法。本文选择非线性时域分析方法，非线性时域分析方法能有效弥补频域分析方法的不足。时域解的第一步是计算风荷载项的抖振力和自激力，并选择准稳态气动力学公式计算抖振力。我们使用Davenport的气动导纳函数来纠正它。然后用谐波综合法模拟风场。本文基于35 m+130 m+35 m单肋连续梁拱组合桥的研究背景。利用数学软件MATLAB和大型有限元软件ANSYS进行数值模拟，研究了连续梁拱桥抖振的非线性行为。考虑结构的几何非线性行为并与线性分析值进行比较。

2 桥梁有限元模型

本文在35 m+130 m+35 m连续梁拱组合桥的基础上进行研究，利用大型有限元软件ANSYS建立了该桥的三维模型。梁单元选择Beam188单元、吊杆选择Link10单元，三维模型中X轴，Y轴，Z轴分别为横桥向，梁高方向和顺桥方向。材料特性如表1所示。图1为全桥模型，对其进行动力计算，得到了桥梁的基本模态(见表2)。

表1 结构材料特性

如表2所示，此桥的基本频率是0.745 Hz，周期是1.342 s，表示此桥整体刚度较大；基频对应的振型为拱肋面外对称侧弯，主梁的横向弯曲比较小，表示此桥主梁的横向刚度比拱肋大；在前六阶振型中拱肋发生扭转，这表明拱肋的抗扭刚度比主梁的小；结构面内振动的基本频率为2.579 Hz，面外振动基本频率为0.745 Hz，面内振动基本频率比面外基本频率大，表示该桥在横向稳定方面存在问题；此桥第一阶扭转出现在第2阶振型，频率为2.056 Hz，出现在面内振型之前，表明此桥梁的抵抗扭转的刚度小于它的面内抗弯刚度。

表2 前六阶振型与频率

3 结构风致响应分析

3.1 风场的模拟

选择谐波合成法来模拟脉动风场的模数值，是一种运算不复杂、理论可靠、结果精度较高的方法。这种方法利用谱分解与三角余弦函数叠加以使数值接近的目的，这样的方法可以较好的模拟随机过程，跨度较大的连续梁拱组合桥的竖向尺寸与顺桥向尺寸通常比横桥向尺寸大的多，所以一般在利用谐波合成法来模拟脉动风场的时候，需要设置数量巨大的模拟点，这样会导致计算很困难。所以我们通过不同结构的特点来简化风场。依据本例的结构特点和振动基本模态，在模拟本组合桥的三维脉动风场时，可以将脉动风场简化为主梁和拱肋沿横桥向和垂直方向的维度为一维的线性随机风速场。利用MATLAB软件使用谐波合成法来模拟出随机风速场。脉动风场在MATLAB中的基本参数如表3所示。主梁跨度为200 m，桥面高10 m，拱肋模拟点为跨中最高点即拱顶。脉动风场模拟基本参数如表3所示。

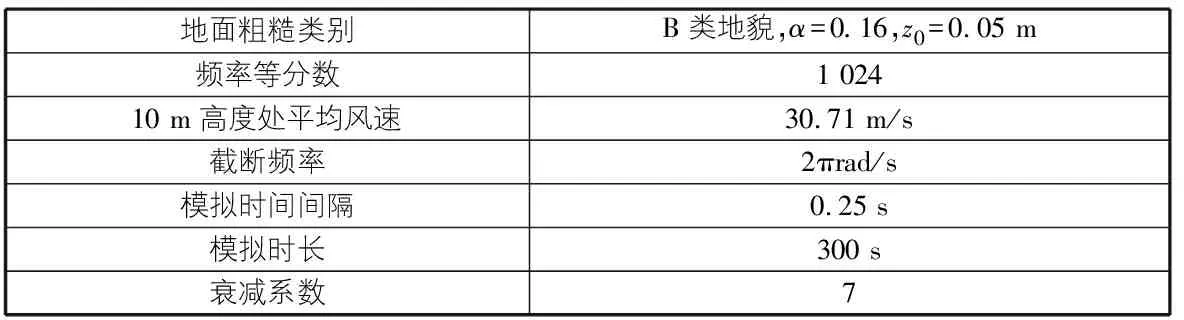
表3 脉动风场模拟基本参数

对MATLAB软件模拟的脉动风场进行分析，该桥拱顶位置前300 s脉动风速时程片段如图2,图3所示，拱顶的水平和竖向脉动风速时程的平均值与0接近(<±0.5 m/s)，如图2，图3所示，脉动风场样本的功率谱密度和目标谱函数的较为吻合，并且验证它的紊流强度和相关数值等都在要求范围之内，这表示该模拟风场符合要求，可以用来进行抖振力的计算和研究。

3.2 抖振力计算

在计算时根据Scanlan准定常气动理论，气动导纳函数将被用来修正结果。此桥单位长度受到的荷载为：

(1)

(2)

(3)

其中，CD′(α),CL′(α),CM′(α)分别为阻力、升力和升力矩对攻角的导数；u(t),w(t)分别为水平和竖向的脉动风速。

加载的时候将抖振力时程加载在拱顶的节点上，并且考虑阻力、升力和扭矩的影响，抖振力时程用式(1)～式(3)进行运算可以算出，把运算得到的结果导入到ANSYS三维模型中，加载到关键节点然后进行分析，得到的模拟脉动风场时间步长和时间的步长一样，一共取300 s，结构阻尼选取规范规定的阻尼比。本组合桥抖振响应运算数据如表4所示。表4中CD，CL，CM均为结构静力三分力系数，CD′，CL′,CM′均为三分力系数对风攻角的导数。

表4 拱顶抖振响应计算的基本参数

3.3 抖振响应分析对比

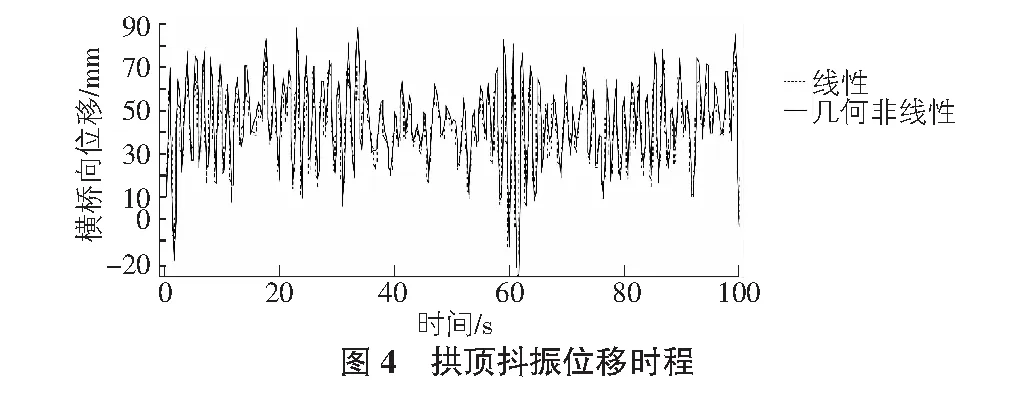
进行抖振时域运算分析，得到梁拱顶部关键部位的横桥向位移与抖振扭转位移时程曲线如图4，图5所示。

把该模型主要节点的位移时程结果利用均方根运算可以得出拱肋顶部的横桥向、垂直方向还有抖振扭转位移响应的数值，如图6～图8所示。

通过上面的数据可以得出，在抖振时域分析计算中，最大跨桥抖振位移峰值和最大抖振扭转位移峰值出现在肋跨度上。 在非线性状态后，拱肋在拱肋横向上的抖动位移略大于线性情况下的拱形抖动位移，拱肋垂直抖振位移的RMS值减小。 拱肋摆动抖动传递RMS值比线性情况稍大，见表5。

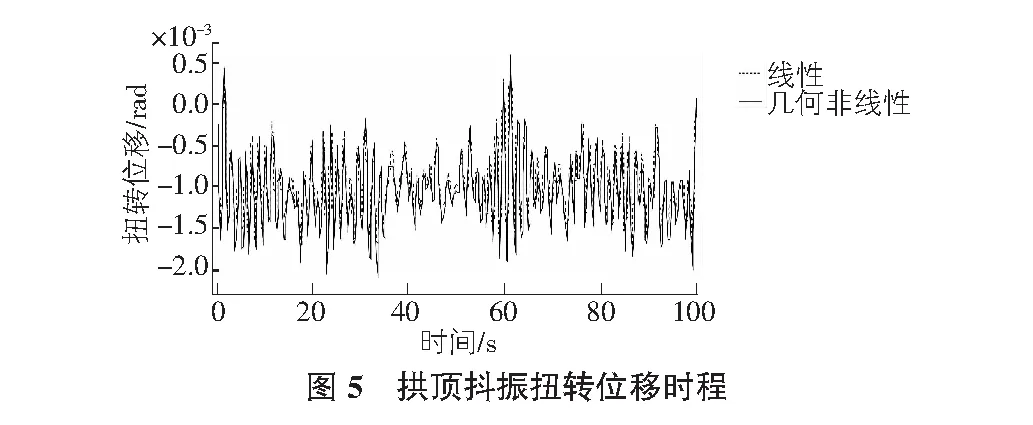
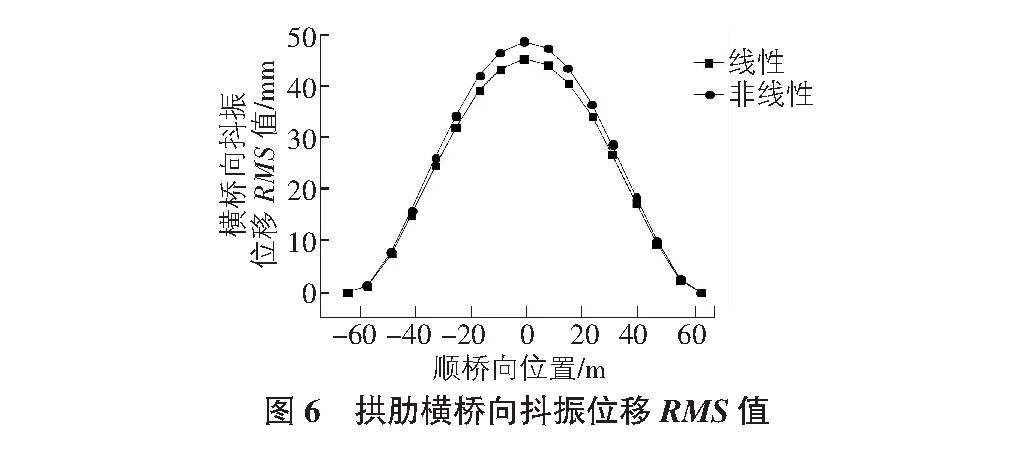
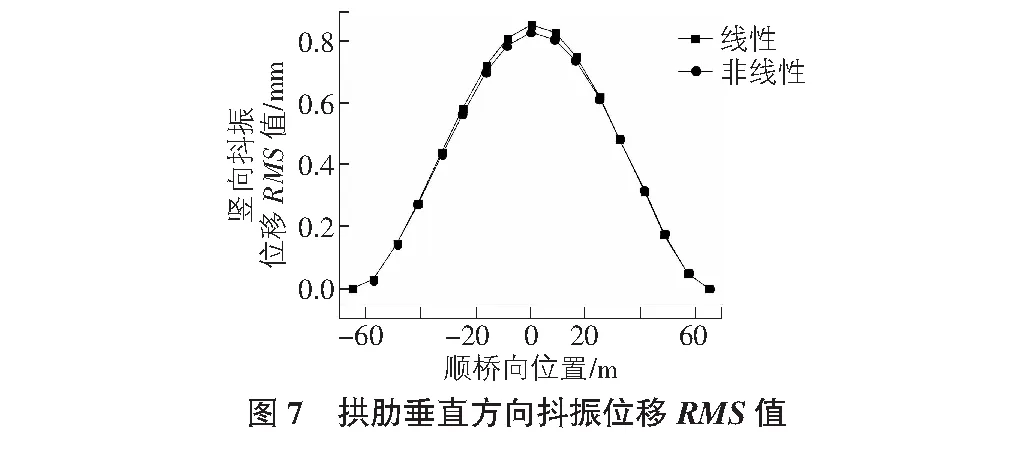
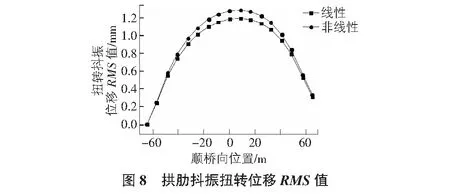
表5 主要截面位置的位移峰值(U=30.71 m/s)

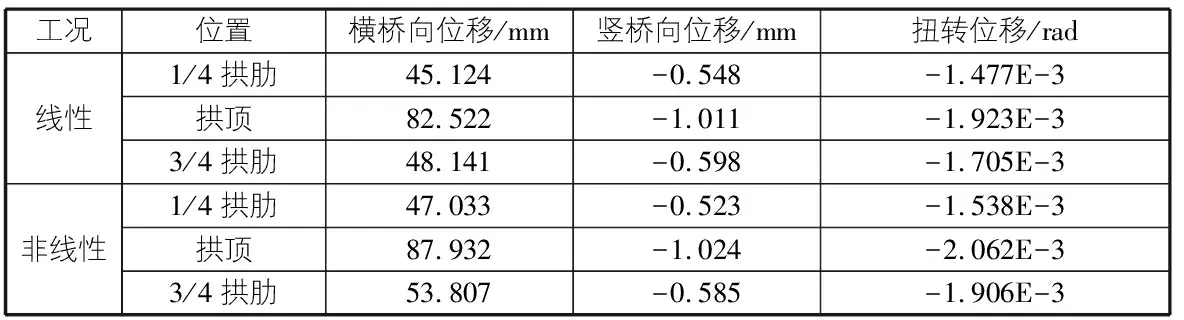
工况位置横桥向位移/mm竖桥向位移/mm扭转位移/rad线性非线性1/4拱肋45.124-0.548-1.477E-3拱顶82.522-1.011-1.923E-33/4拱肋48.141-0.598-1.705E-31/4拱肋47.033-0.523-1.538E-3拱顶87.932-1.024-2.062E-33/4拱肋53.807-0.585-1.906E-3

考虑到非线性情况，比较抖振内力响应的峰值，可以看出桥梁主要部分的轴力没有明显变化。右拱脚的垂直弯矩增加11%，右拱脚的力矩沿桥向增加12%，其余内力峰值几乎没有变化，见表6。

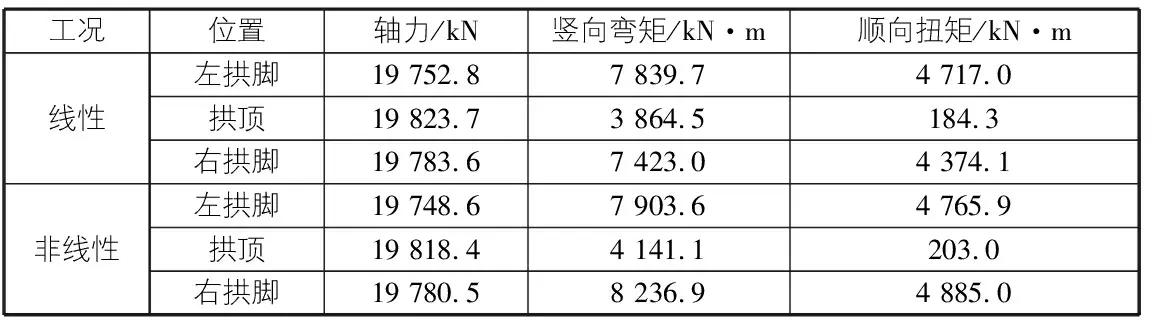
表6 主要截面位置的内力峰值(U=30.71 m/s)

4 结语

本文主要计算和分析连续梁拱组合桥的风致抖振响应。首先，进行脉动风场的数值模拟，然后将抖振力施加到桥上，并且优先进行抖振响应分析，得到了如下几条结论：

1)在抖振时域分析计算中，最大跨桥抖振位移峰值和最大抖振扭转位移峰值出现在肋跨度上。 在非线性状态后，拱肋在拱肋横向上的抖动位移略大于线性情况下的拱形抖动位移，拱肋垂直抖振位移的RMS值减小。 拱肋摆动抖动传递RMS值比线性情况稍大。

2)考虑到非线性，比较抖振内力响应的峰值，可以看出桥梁主要部分的轴力没有明显变化。右拱脚的垂直弯矩增加11%，右拱脚的力矩沿桥向增加12%，其余内力峰值几乎没有变化。

3)在设计风速范围内，随着风速的增加，交叉桥扭转振动和拱肋扭转振动的RMS值增大。垂直位移没有明显变化，表明风速对大跨度连续梁拱组合桥的横向和扭转位移有很大影响。 对竖向位移无明显影响。