分时电价和时变行程时间下的供应链调度
2018-12-11王君
王 君
天津财经大学管理科学与工程学院,天津,300222
0 引言
经济与社会的持续发展带来能源消耗的快速增长,与此伴随的CO2排放是全球气候变化的重要因素。工业生产的能源消耗达到全球总能源消耗的一半[1]。在大多数生产企业中,电力是消耗能源的主要形式[2]。电力不能被有效存储,只能随着用户的需要而进行实时的生产、运输和供应,因此,需求反应技术和负荷管理对电力供需的平衡十分重要,分时电价(time-of-use electricity tariffs,TOU)政策就是一种最常用的策略[3]。它通过价格机制,鼓励电力需求敏感的消费者把电力使用从需求的波峰时段移动到波谷时段,从而有效提高电网系统的稳定性和效率。
TOU政策下,制定生产计划需要考虑订单(或机器、工序)的功率消耗,尽量把高功率的订单放在低电价下进行生产,以达到节省电力成本的目的。FANG等[4]以最小化电力成本为目标,研究了单机器生产环境下的抢占式和非抢占式机器调度问题,证明了问题的复杂度并给出了精确的或近似最优的求解算法。CHE等[5]对类似的单机器非抢占式机器调度问题,设计了一个贪婪插入算法。WANG等[6]针对生产批次的调度问题,在最小化电力总成本的同时,增加了总完工时间目标,给出了一个得到精确Pareto前沿的算法。DING等[7]以同样的两个优化目标研究了平行机生产系统的机器调度问题,给出了求解多目标问题的启发式算法。
生产系统有效利用电力、保持电网稳定性是实现节能减排的方式之一。对工业企业而言,另一个节能减排方式是在配送系统中节约燃油。UBEDA等[8]在配送系统的案例研究中指出,仅通过减少总行驶里程就能比初始的配送方案减少25.5%的燃油消耗。城市配送中,道路网络的拥堵程度类似于分时电价,选择较通畅的时段进行配送有利于减少油耗[9]。因此,企业有效整合生产和配送系统,有利于同时节约电力和燃油总成本,以实现可持续调度[10]。对生产和配送同时进行决策的问题称为供应链调度问题[11],这明显增加了问题的复杂程度,但目前的研究都没有考虑分时电价和路网的拥堵[12-13]。
本文针对单机器、单客户的供应链调度问题,考虑在分时电价政策和路网拥堵的条件下,对工件的开始生产时刻、配送的批次和开始配送时刻进行决策。以最小化生产电力成本与配送油耗成本之和为目标建立模型,然后分析模型的优化性质。基于模型的最优性质,把集成的模型分解为多个批次的机器调度子问题。对于子问题的优化,设计了一个子集划分的启发式算法;对于主问题的优化,设计了自适应变邻域搜索算法。数值计算表明,供应链调度模型和算法比先优化生产调度、后优化分批配送的分阶段优化方法,可节约更多的电力和油耗成本。
1 问题描述
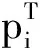
分时电价指每个时段的电力价格随着电力需求的不同而变化。把加工周期划分成m1个时间段,第k(k=1,2,…,m1)个时间段记为Tk,该时间段的结束时刻记为ek。那么Tk可以表示为时间区间[ek-1,ek],Tk内的单位电价为ck。假设任意一个工件的加工时间都小于Tk。分时电价下,不同时间段安排工件的加工所耗费的电力成本是不同的,因此生产决策包括工件的加工顺序和每个工件的开始加工时刻。
时变行程时间(time-dependent travel times,TDTT)可描述路网的拥堵。车辆行驶在某个配送路段的行驶速度依赖于路网的通畅程度。把配送周期分成m2个时间段,第η(η=1,2,…,m2)个时间段pη的结束时刻记为lη,同样可以用区间[lη-1,lη]表示pη。假设在任意完整时间段内都可以完成配送任务,即车辆在配送时最多横跨2个时间段。根据ICHOUA等[14]的TDTT模型,在pη内,车辆的行驶速度为sη。该模型把行驶速度表示为时间的分段函数,使得模型具有先进先出(first in first out,FIFO)性质,即先出发的车辆一定比后出发的车辆先到达目的地。路网拥堵条件下,在不同的加工完成时刻安排配送分批,每个配送车辆对应的载重、行驶速度是不同的,所以其耗费的燃油成本也是不同的。因此,在生产决策已知的情况下,配送决策即为确定配送的批次。
2 模型建立
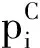
(1)
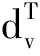
(2)
其中,yiv是0-1决策变量,如果工件i由第v个批次进行配送,则yiv=1;否则,yiv=0。
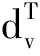
(3)
αη=γ0+γ1sη
(4)
(5)
式中,D为工厂到客户的行驶路线长度;αη、βv为油耗系数;γ0、γ1为与速度相关的参数,γ0≥0,γ1≥0;μ为长期统计的车辆载货量;λ0、λ1为与载重相关的参数,λ0≥0,λ1≥0。
显然,在其他条件不变的前提下,随着速度的增大,αη增大,油耗减小;随着载重量的增大,βv减小,耗油增大。
记h为燃油价格;Csum为加工和配送所有工件的总成本;M为无穷大的数;xij为0-1决策变量,即如果工件i在工件j之前进行加工,并且在工件i与工件j之间无其他工件,则xij=1;否则,xij=0。考虑其他约束,该问题的混合整数规划模型如下:
(6)
s.t.
(7)
(8)
(9)
(10)
(11)
(12)
xij+yiv≤1+yjv+yj,v+1
(13)
xij∈{0,1}
(14)
yiv∈{0,1}
(15)
zi≥0
(16)
模型中,式(6)表示优化目标是最小化加工和配送的总成本;式(7)表示机器加工第一个工件的顺序约束;式(8)、式(9)表示机器加工其他工件的顺序约束;式(10)表示每个工件必须包含在一个配送批次中;式(11)表示每个批次的配送量不能超过车辆的载重能力;式(12)表示前一个工件完成加工后,才能开始加工下一个工件;式(13)表示相邻加工的后一个工件,要么与前一个工件一个批次配送,要么在下一个批次进行配送;式(14)、式(15)是0-1变量约束;式(16)是非负变量约束。
3 模型的求解分析
分析模型及解的性质有利于构造高效的优化机制,减小搜索空间,提高算法的效率。该优化问题包含生产调度和分批配送两个有先后顺序的决策子问题,首先对这两个子问题进行求解分析。
定义1如果工件的开始加工时刻和加工完成时刻都包含在时间段Tk内,那么称该工件在Tk内完全加工;如果工件的开始加工时刻在Tk内,加工完成时刻在Tk+1内,则称该工件横跨时间段Tk和Tk+1,并称该工件在Tk和Tk+1部分加工[5]。
定义2如果工件i的加工完成时刻等于工件j的开始加工时刻,那么称工件i和j是紧密相邻的,并称工件i是j的紧前工件,工件j是i的紧后工件。
定义3如果在加工序列(i1,i2,…,is)中,任意相邻的两个工件都是紧密相邻的,且i1无紧前工件,is无紧后工件,则称该加工序列为紧序列,工件个数s(s≤n)称为该紧序列的长度。如果紧序列(i1,i2,…,is)中的某个工件is′横跨时间段Tk和Tk+1,则称(i1,i2,…,is′)和(is′,is′+1,…,is)分别是在Tk和Tk+1内的紧序列。
定义5如果模型的最优解唯一,那么称该最优解为最优决策方案;如果最优解不唯一,那么称含有紧序列数量最少的解为最优决策方案。
引理1加工某个工件的电力成本仅取决于各个时间段加工该工件的时间消耗[5]。
引理2若某个工件在一个时间段内加工完成,则加工该工件的电力成本与开始加工时刻无关[5]。
定理1如果模型存在最优解,那么最优决策方案存在以下性质:
性质1在时间段Tk内的某个紧序列中,任意交换同一配送批次、完全加工工件的次序,模型的最优值保持不变。
性质2在时间段Tk内,完全加工的非关键工件与同一批次的关键工件必定组成一个紧序列。
性质3如果一个同批次配送的加工序列(i1,i2,…,is)是紧序列的一部分,序列中某个工件is′横跨时间段Tk和Tk+1。若ck
位于一六多金属矿田南部、天门坳—牛公锥西主干断裂中段西侧、梅子冲银铅锌矿床南约4km处(图1)。赤老顶锑矿历史悠久,于清末始被发现和开采,矿体主要呈似层状、透镜状赋存于天子岭组内的硅化层或硅化断裂破碎带中,主矿体赋矿标高为409~134m,目前最深开采标高至+170m左右。断裂发育,具有近SN、NNE、NNW、NW、近EW及NE向等多组断裂,其中近SN向、NNE向、NNW向组与矿化关系较密切。围岩蚀变主要为硅化、方解石化。区内未见岩体出露。
性质4如果一个同批次配送的加工序列是紧序列的一部分,序列中的工件is′横跨时间段Tk和Tk+1。若ck
根据引理1和引理2容易得到定理1中的性质1和性质2。图1给出了性质2的示例。在a行中,5个工件在时间段Tk内完全加工,分2个批次进行配送,根据引理2,往后推移工件1和2的开始加工时刻使工件1、2、3紧密相邻,往后推移工件4的开始加工时刻使工件4、5紧密相邻,得到2个紧序列,如b行所示。由于关键工件3和5未移动,所以加工和配送这5个工件的总成本不变。在c行中,6个工件组成了1个紧序列,含有2个关键工件,示意了1个紧序列由多个配送批次组成。

图1 性质2的紧序列示意图Fig.1 A compact sequence diagram of property 2
从以上分析可以看出,在不改变成本的前提下,时间段Tk内,完全加工的非关键工件的开始加工时刻具有一定的灵活性。如果可以,把它们的开始加工时刻在Tk内往后(即时间轴方向)推移,直到与所在批次的关键工件组成紧序列;否则,就把它们的开始加工时刻在Tk内往前(即时间轴相反方向)推移,直到与前1个批次的关键工件组成紧序列。
以上分析的目的是为了在多个最优解中,选出最优决策方案作为优化的最终结果。最优决策方案相比于其他最优解,含有最少的紧序列,所以机器的加工间歇期最少,从而尽量减少机器在加工和间歇状态之间的转换,这符合现实企业的操作实践。
性质3由反证法容易证明,由性质1和性质3易得到性质4。根据以上分析可知,在最优决策方案中,序列内工件的次序不唯一。为了在研究中得到最优决策方案的唯一解,对某同批次配送的加工序列(i1,i2,…,is)进行分析,如果它是紧序列的一部分,不失一般性,本文约定:①如果该序列在时间段Tk内,那么序列内工件按照加工功率升序排列;②如果该序列中的工件is′横跨时间段Tk和Tk+1,那么序列内工件在ck>ck+1时,按加工功率升序排列;在ck 由于FANG等[4]已经证明分时电价下的机器调度问题是NP-Hard问题,所以本文研究的供应链调度问题也是NP-Hard问题。因为基于邻域搜索的算法在处理生产、配送分批调度问题中具有很好的优化效果[15-17],所以本文采用文献[18]提出的自适应变邻域搜索(adaptive variable neighborhood search,AVNS)算法的框架进行求解。 采用基于配送批次和开始配送时刻的向量组编码结构,用第v个向量表示车辆v配送的工件,最后一个向量表示每个批次的开始配送时刻。例如,向量组((2,5),(3,7,9),(1,4,6,8),(100,180,360))表示9个工件、3个批次的调度方案,具体加工配送调度计划如图2所示。机器加工完工件2、5后,在时刻100配送第1批工件;加工完工件3、7、9后,在时刻180配送第2批工件;最后加工工件1、4、6、8并配送它们。该编码结构下,每个批次工件的加工顺序可以是任意的,但要求每个批次最后一个工件的加工完成时刻等于该批次的开始配送时刻。为了得到每个批次的工件加工次序和工件的开始加工时刻,需要对向量组解码以获得模型的解。通过定义6和算法1,可以对向量组的每个分批进行解码。 图2 向量组表示的调度计划示意图Fig.2 The diagram of a scheduling plan expressed by a vector group 定义6根据向量组编码结构,对于某个分批,在已知机器准备就绪时刻、加工完成时刻的条件下,确定该批次每个工件的开始加工时刻,以最小化该批次生产电力成本为目标的优化问题称为分时电价下加工完成时刻已知的机器调度问题(子问题1)。 算法1机器调度算法 (2)对工件按照加工功率降序排序得到排列i1、i2、…、is。 (3)Forl=1 tosdo ②把工件il的加工完成时刻设置成时间轴的结束时刻,更新Is′和Is′-1。 ③Forl′=1 tosandl′≠ldo b.选择电力成本增量最小的时间段、插入方式,插入工件il′。 c.Fork=1 tos′ do更新Ik。 ④计算该批次工件的加工电力成本f(il)。 (4)选择最小的f(il)对应的方案。 (5)Forl′=1 to s andl′≠ldo依据性质2、性质4和最优决策方案唯一解的约定,计算工件l′的开始加工时刻,算法结束。 定理2如果电价是按照批次内时间段升序或降序排列,那么用算法1可以计算得到子问题1的最优解;否则,可以得到子问题1的近似最优解。 证明:显然步骤②是把问题的解集划分为s个子集,在每个子集中,安排工件il为最后一个加工工件,对其他工件的加工调度转化为一个分时电价下的非抢占式机器调度问题(子问题2)。 对子问题2,算法1的步骤(1)(2)和步骤②~④组成的算法与贪婪插入启发式算法[5]一致。因为CHE等[5]通过实验验证了算法的近似最优性,而且步骤(5)不改变工件在每个时间段的加工时间,即加工成本不变。因此,通过步骤(4)(5)可以求得所有子集近似最优解的最小值(子问题1的近似最优解)。 为了得到可行的调度方案,采用算法1的部分步骤得到加工计划,然后进行批次分配,具体步骤如算法2所示。 算法2初始解生成算法 (1)依次执行算法1的步骤(1)(2)和步骤②~④、步骤(5),得到加工计划序列(i1,i2,…,in)。 (2)初始化l:=1,v:=1,Load:=0。 (3)Whilel≤ndo ②置l:=l+1。 (4)利用算法1优化每个批次的机器调度问题。 在每个批次包含的工件和批次的开始配送时刻已知的条件下,根据机器调度算法,能得到供应链调度问题的最优解或近似最优解。因此,对供应链调度问题的全局优化,就简化为对开始配送时刻的搜索和对批次分配的搜索,这是邻域结构设计的出发点。 定义7对某个工件的开始配送时刻附近进行搜索的邻域,称为开始配送时刻邻域。 假设配送批次v最后一个加工的工件为工件i,工件i所在的紧路径中任意的一个工件为工件j,即j∈Jj,其中,Jj为工件j所在紧路径中所有工件的集合,那么有 算法3开始配送时刻邻域 (1)随机选择配送批次v,得到该批次最后一个加工的工件i,假设包含该批次的紧序列包含的批次为v-s、v-s+1、…、v+s′-1、v+s′(s,s′≥0)。 (2)在时间轴方向或时间轴相反方向中随机选择一个搜索方向。 (5)利用算法1优化每个批次的机器调度问题。 定义8把一个批次中的某个工件移动到另一个批次称为批次移动邻域。交换2个批次中的某个工件称为批次交换邻域。批次移动邻域和批次交换邻域统称为批次邻域。 记邻域u(u=1,2,…,U)的选择概率为ρu,邻域u的有效、无效的次数分别为ρ1,u和ρ2,u。令有效率ρ3,u=ρ1,u/(ρ1,u+ρ2,u)+0.02,那么[18] (17) 根据以上自适应选择机制,结合4.1、4.2节的内容,得到如下AVNS算法的总流程: (1)初始化批次移动和批次交换的有效次数ρ1,1=ρ2,1=5、无效次数ρ1,2=ρ2,2=5。利用算法2生成初始解X,并设置X为当前解和最优解。初始化φ:=0。 (2)Whileφ<φmax ①根据两个批次邻域的选择概率,使用轮盘法随机选择一个邻域u。 ②Forθ=1 toθmaxdo a.使用邻域u对当前解进行邻域操作,得到解X′。 b.使用算法3的开始配送时刻邻域对X′进行局部搜索,得到的最好解记为X″。 c.如果X″优于当前解,则置ρ1,u:=ρ1,u+1;否则置ρ2,u:=ρ2,u+1。 d.置X″为当前解,φ:=φ+1。如果X″优于最优解,则置X″为最优解,φ:=0。 ③使用式(17)更新邻域的选择概率。 随机生成参数不同的18个算例,来验证模型的正确性、算法的效率以及对问题规模的敏感程度。算法用Visual C# 2010编程,在Intel i7-6700 3.4 GHz的CPU、8GB内存、Windows7系统的电脑上运行。设置工件数量为20、40,随机生成工件的相关参数,各参数的取值范围如表1所示。为了在加工周期内完成所有工件的加工任务,随着工件的增加,每个工件的平均加工时间缩短。工件的加工功率设置为高功率、低功率、高低功率混合三种类型,工件质量也有类似设置。设置车辆最大载重Qv=20 t,行驶路线长度D=100 km,油价6元每升,分时电价[5]和时变行程时间的设置如表2所示。与油耗相关的参数如下[9]:λ0=4.400 276 59,λ1=0.000 033 978 4,γ0=4.537 757 841 4,γ1=0.065 805,μ=15 173.04 kg。参考文献[15,17-18]对算法参数的设置,令θmax=3,4,…,9;φmax=10,20,30,40,并选取几个算例进行试优化。我们发现θmax的取值对算法优化结果的影响不大,较大的φmax会增加算法的运算时间,因此,经过反复试验后设置算法参数:θmax=5,φmax=20。 表1 工件参数 表2 分时电价和时变行程时间参数 如表3所示,算法的计算结果分为两部分:一部分是运用本文提出的供应链调度优化模型和AVNS算法得到的计算结果;另一部分是把加工调度和批次配送调度分成两个阶段先后优化,即先采用文献[5]的方法优化加工调度,然后在加工计划给定的条件下优化分批得到的计算结果。优化分批采用本文提出的ANVS算法框架和相同的参数设置,其算法中邻域结构的设置如下:①将某个批次的第一个工件移动到前一个批次;②将某个批次的最后一个工件移动到后一个批次。表3中,加粗字体显示较好的结果。从计算时间上看,作为对比的分阶段优化算法用时很少,这是因为文献[5]采用的是贪婪插入算法,缺少全局搜索过程。从总成本的对比结果看,以供应链整体视角进行的优化比分阶段优化减少4.85%~18.47%的成本。再分别对加工和配送的成本进行分析。供应链整体优化的配送成本都明显小于分阶段优化的成本。算例2a、2b、3a、6a、7a、7b的分阶段优化的加工成本大于整体优化方式,这是因为在时间段较多并且电价不是按照时间段有序排列的情况下,用文献[5]的算法优化加工调度仅能取得近似最优解。整体优化方式仅在批次内部进行加工调度的优化,而每个批次的时间区间包含的时间段要少很多,那么配送成本就进一步接近甚至等于最优解。因此,本文提出的供应链整体视角的优化模型和AVNS算法在优化加工和配送总成本方面具有很好的效果。 表3 算例计算结果 由表3可知,当工件较少(20个工件)时,AVNS算法在30 s内就能取得最终结果。当工件数量增加到40时,运算时间明显延长。这是因为运算时间主要取决于邻域的搜索范围和算法的迭代次数。批次较多或配送成本明显大于加工成本,会增加邻域范围和搜索的深度。算例8b同时满足以上两个条件,其运算时间最长,但也没有超过10 min,其运算过程见图3。在前50次迭代中,总成本目标的下降速度较快,下降到4 196.52 元,已经优化了97.64%,说明AVNS算法在运算过程的前期具有较好的优化效果。在运算后期,当前解在最优解上方随机波动,说明AVNS算法的随机搜索性能较理想。 图3 算例8的迭代过程Fig.3 Iterative process of example 8 (1)在分时电价政策和时变行程时间下,研究了单机器的集成生产计划和配送分批的供应链调度问题,对每个工件的开始加工时刻、配送的分批进行决策,目标是优化总成本。 (2)建立了混合整数规划模型,分析了模型的最优化性质,设计了自适应变邻域搜索算法进行求解。数值计算的实验表明,供应链集成调度模型比分阶段先后独立优化具有很大的优势。 (3)对单机器、单个客户的供应链调度问题进行了研究。由于企业的生产系统、配送系统具有多样性,考虑多机器、多客户、车辆路径规划等条件下的供应链调度问题,是下一步研究的方向。4 模型的求解算法
4.1 解的编码结构及解码
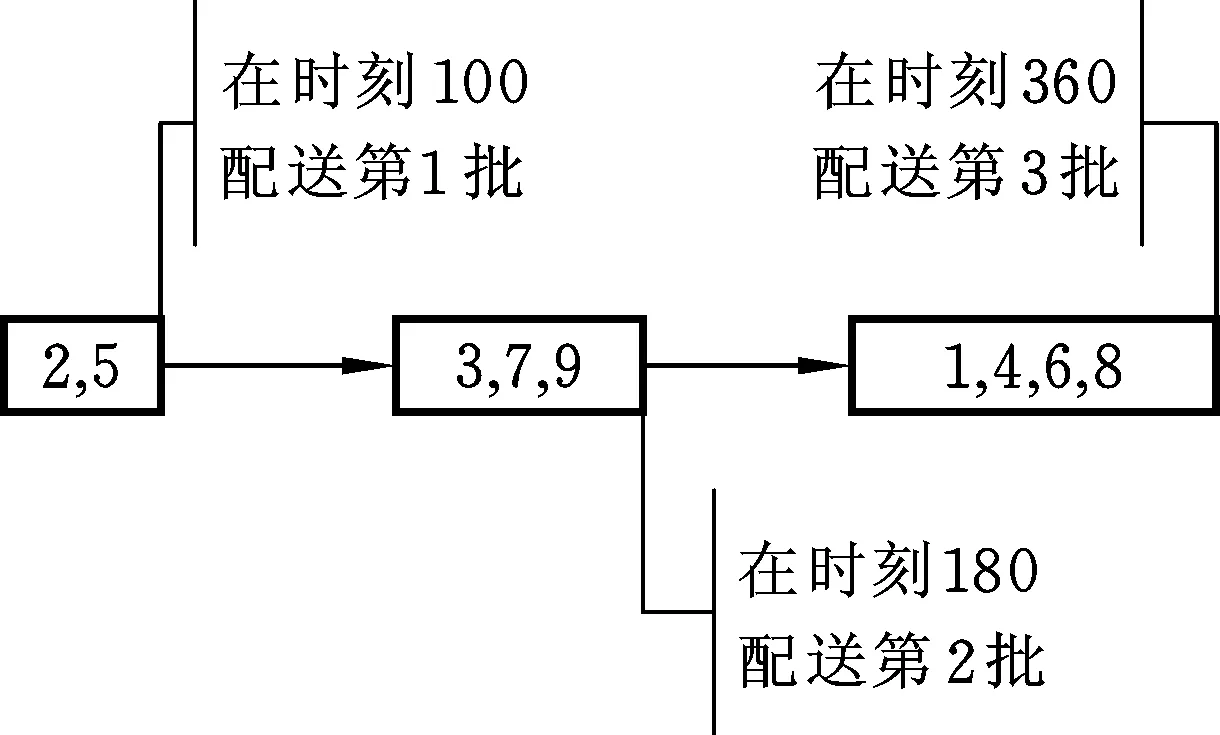




4.2 初始解
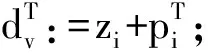
4.3 邻域结构
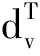
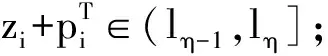
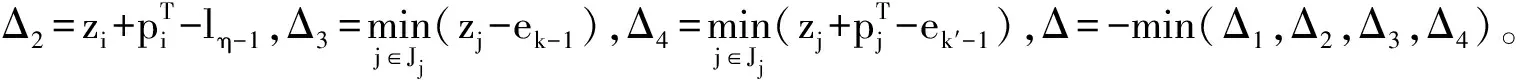
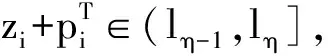
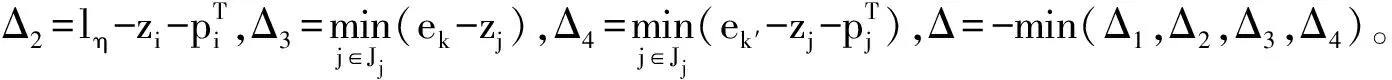
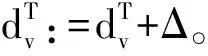
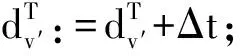
4.4 AVNS算法总流程
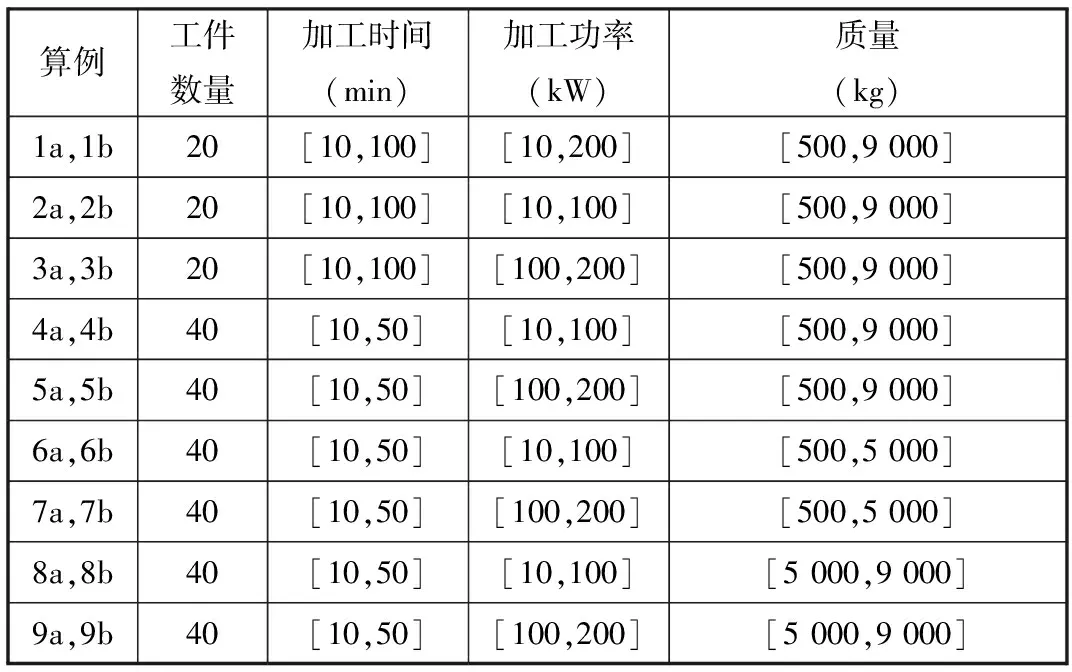
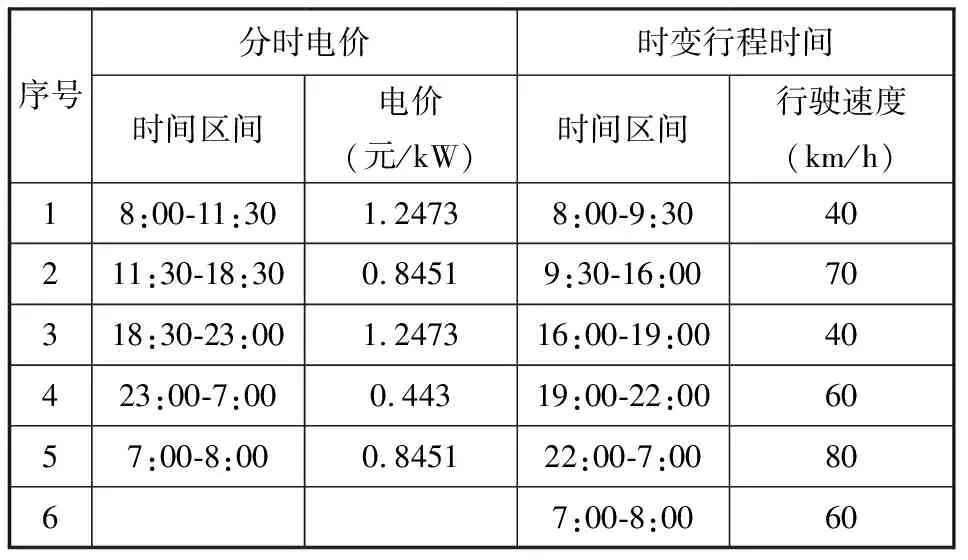
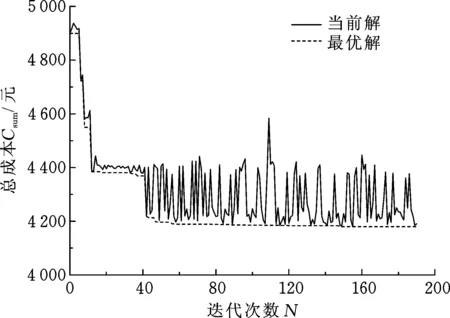
5 数值计算分析

6 结论
