装卸一体化车辆路径问题的自适应并行遗传算法

周 蓉 沈维蕾

合肥工业大学机械工程学院，合肥，230009

0 引言

装卸一体化车辆路径问题(vehicle routing problem with simultaneous pickup and delivery,VRPSPD)是车辆路径问题的一类重要扩展。该问题涉及的客户同时具有送货和取货两种需求，且要求服务车辆将产品配送至客户的同时从该客户处取走其他物品，如汽车、家电等行业制造商将新产品运送至客户，同时回收客户的废旧产品[1]。该问题不受送货与取货先后顺序的限制，能有效减少车辆空载、降低运作成本并提高服务效率[2]。但是双重需求及波动变化的车辆承载特征使得问题结构明显不同于单一需求的车辆路径问题，它涉及更为复杂的客户分配和车辆载重量界定，求解难度更大[3]。

国内外有关VRPSPD的文献较多，求解目标多以最小化车辆行驶距离为主，但现实中可能存在由租赁费用产生的单次派出成本，需要综合考虑单次派车成本和配送路径成本。虽然少数文献增加了车辆数目方面的分析，但缺乏对总配送成本、车辆数目、车辆行驶距离等多种目标的系统性分析。如TASAN等[4]以最小化车辆行驶距离为目标，提出一种基于遗传算法的方法来求解VRPSPD，并利用Augerat标准数据集部分算例进行验证，结果证明该方法较数学规划工具Cplex具有更好的稳定性。NAGY等[5]提出采用插入式启发式方法求解单个/多个车场的带回程车辆路径问题，并设计了包含VRPSPD问题在内的5类标准数据集。柳毅等[6]提出采用改进人工鱼群算法求解相同目标问题，并利用NAGY标准数据集中的10组算例进行仿真分析，结果证明该算法虽然计算时间较长，但寻优性能较文献[5]的插入式启发式算法更加优越。彭春林等[7]在求解VRPSPD问题时增加了派出车辆数目标，但对算法的性能分析只针对NAGY标准数据集中的两组算例，算法验证缺乏普适性。龙磊等[8]针对相同目标问题提出采用一种粗粒度并行遗传算法进行求解，并以NAGY标准数据集中的14组算例进行验证，证明该算法在大部分实例上超过了已知最优解。TANG等[9]以最小化车辆数目、最小化车辆行驶距离为目标，提出采用一种基于局域迭代搜索的禁忌搜索算法进行求解，并以多个标准测试集进行了算法准确性和有效性的验证。WASSAN等[10]提出一种能自动调节禁忌长度的自适应禁忌搜索算法，结果表明该算法性能在绝大部分算例上优于文献[9]的禁忌搜索算法。WANG等[11]以最小化总配送成本、最小化车辆数目、最小化车辆行驶距离为目标，并考虑时间窗约束，提出采用联合进化遗传算法进行求解，结果表明该方法较基本遗传算法和数学规划工具Cplex具有更好的寻优性能。

上述研究表明，VRPSPD问题的优化目标多以配送距离为主，部分文献考虑了配送车辆数目，几乎没有文献将配送距离、车辆数目及配送成本进行系统性分析；求解算法大多集中在以经典C-W节约法为基础的启发式方法和以群体智能为基础的元启发方法。遗传算法(genetic algorithm，GA)作为一种鲁棒性较强的元启发方法，在许多车辆路径与调度问题的求解应用中已被证明具有良好的优化性能[4,7-8,11]。GA在搜索处理后期容易出现两难窘境：要么收敛速度较慢耗时长，要么早熟收敛陷入局部最优，因此，必须在进化过程中改善种群的多样性和优良基因的遗传性，以提高算法整体搜索性能[7,11]。受到该思想的启发，本文将包含多样性种群和高质量种群的双种群并行策略引入基本遗传算法，提出一种自适应并行遗传算法求解包含多种目标的VRPSPD问题，并通过算例仿真和结果对比验证所提算法的可行性和有效性。

1 问题描述与模型

VRPSPD问题可以描述如下：物流中心拥有一定数量的相同车辆，车辆从配送中心出发，在一定时间内完成确定数量客户集的送货与取货后返回物流中心。每个客户的送货与取货由同一车辆同时完成。要求合理安排车辆配送路线，在派出车辆数目最小、车辆行驶距离最短的情况下，实现总配送成本最小。采用符号体系描述如下：假设物流中心共有N个客户，采用i、j表示客户编号(i，j=1，2，…，N)，0表示物流中心；Z为总配送成本；客户的送货量和取货量分别为di、pi；客户之间的距离为cij，物流中心到客户i的距离为c0i；车辆单位距离行驶成本为g，单车指派成本为f，最大装载量为Q；车辆总数为K，车辆k(k=1，2，…，K)离开客户i时车上载重量为Uik，车辆的最大行驶距离为L。

根据上述描述，建立VRPSPD问题的混合整数规划模型如下：

(1)

满足约束条件：

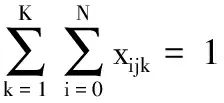
(2)

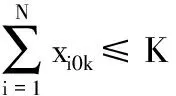
(3)

(4)

(5)

∀i=0,1,…,N;k=1,2,…,K

(6)

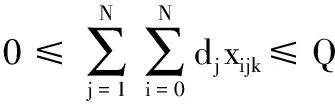
(7)

(8)

(9)

(10)

Uik≥0 ∀i=0,1,…,N;k=1,2,…,K

(11)

式(1)考虑了车辆指派成本、运输路径成本的总配送成本Z最小目标，隐含车辆数目最小、车辆行驶距离最短两个子目标；式(2)确保每个客户只被服务一次且仅由一辆车服务；式(3)确保使用车辆数不超过车辆总数K；式(4)为流量守恒式，即到达和离开每个客户的车辆相同；式(5)～式(8)为容量约束，式(5)表示当xijk=1时，确保车辆k在离开客户i后，服务客户j时车上载重量不超过车容量Q；式(6)表示任何一辆车服务的所有客户的货物都是由物流中心配送的，保证车辆从物流中心出发时的载货量等于其所服务的客户的送货需求量之和；式(7)、式(8)分别确保每辆车服务的所有客户送货需求量总和、集货需求量总和均不超过车容量Q；式(9)为车辆最大行程约束；式(10)和(11)为决策变量属性。

2 自适应并行遗传算法

2.1 双种群并行策略

为解决GA在搜索过程中出现的两难窘境，本文提出一种包含多样性种群和高质量种群的双种群并行策略，其中多样性种群以改善种群多样性为主要目的，高质量种群以强化寻优能力为主要目的。双种群并行策略框架结构见图1。该策略通过对双种群同时执行不同的遗传操作(针对多样性种群执行多样性交叉变异操作、针对高质量种群执行自适应交叉变异操作)，并针对双种群中最优个体执行特殊变异和后优化的局域搜索，使得算法在扩大搜索空间的同时能够进行深度搜索并保持优良基因的遗传性状，从而有效避免陷入局部最优。

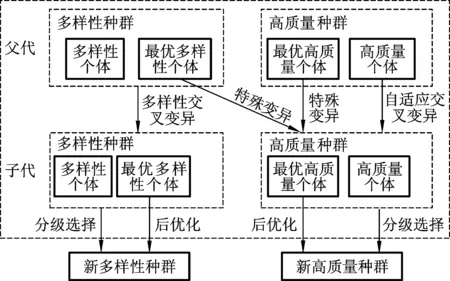
图1 双种群并行策略框架结构Fig.1 Frame structure of bi-group parallel strategy

2.2 编码及解码

染色体结构为N个1～N之间互不重复的自然数排列(N为客户总数)，该排列是一条以自然数序列表示客户服务顺序的无分段大路径[12-13]。染色体解码采用基于深度优先搜索的大路径分割方法[14]，考虑车辆装载能力、最大行驶里程等约束。

2.3 种群初始化

由于初始解质量对遗传算法求解的速度和质量影响较大，本文以C-W节约法为基础，设计3种基于双重需求的启发式种群初始化方法，并采用大部分个体随机生成、部分优良个体采用种群初始化方法生成的方式得到初始种群。随机产生方法遵循两条原则：第一，不允许产生相同个体；第二，随机产生个体与已产生个体的目标值之差应不小于某一数值Δ[13]。

2.3.1基于双重需求的最低成本插入法

C-W节约法根据待插入位置所能带来的成本(或距离)节约值中的最大值来决定最佳插入位置[15]。为降低车辆超载率并提高车辆装载率，VRPSPD客户服务排序须考虑集货量与送货量之间的关系，通常将具有较大配送需求、较小取货需求的客户提前安排，或将具有较大取货需求、较小送货需求的客户延后安排。本文设计了一种基于双重需求的最低成本插入法(简称PDCW法)，新的节约值根据取货量与送货量之间的关系对客户在不同插入点产生的空间效益差异影响进行定义，其计算公式为

(12)

Sij=c0i+c0j-cij

2.3.2基于双重需求的多参数最低成本插入法

PDCW法虽然考虑了客户需求量对改进节约值的不同影响，但未考虑不同节点之间运输费率或运输距离对节约值的权重影响。MESTER等[16]提出了一种改进OSMAN节约值[17]的多参数最低成本插入准则，插入点的成本节约值受到插入点与其紧前、紧后节点之间成本(或距离)的权重影响。受此启发，本文设计了一种基于双重需求的多参数最低成本插入法(PDMPCW法)，通过同时考虑客户需求量及新弧对节约值的影响程度来改进成本节约值。改进后的成本节约值计算公式为

(13)

2.3.3基于双重需求的多参数随机最低成本插入法

为了在搜索空间中产生多个较为分散且质量优良的初始染色体，本文提出基于双重需求的多参数随机最低成本插入法(PDMPRCW法)。该方法以PDMPCW法为基础，先将染色体前面k个客户固定，后面N-k个客户采用PDMPCW法根据最大成本节约值准则插入。k的取值根据客户总数N，按一定百分比可以取不同的整数值，如N=34时，k按0.3N,0.4N,…,0.9N进行向上取整，将分别得到固定前11、14、17、21、24、28、31个客户的7条染色体。

2.4 适应度值

总配送成本同时受到车辆派出数量和配送路径距离的影响。相比具有较低车辆派出数量的父代，优良子代更容易从具有较短配送距离的父代染色体中遗传优良基因。为有效避免早熟收敛并体现不同染色体的配送路径距离在整个种群中的影响，本文采用配送路径距离在整个种群中的评级，同时考虑种群大小的方式确定适应度值。适应度值的计算公式为

FitV(x)=PS-Rank(x)

(14)

其中，FitV(x)表示染色体x的适应度值，PS表示种群大小，Rank(x)表示染色体x的配送路径距离在整个种群中的评级，即配送路径距离在种群中按从小到大排序后的级别。如染色体x的配送路径距离在种群中的排序为5，则Rank(x)=5。

2.5 交叉操作

交叉操作是产生新个体并将优良基因遗传给子代的主要方法，是决定算法收敛性能的关键。针对多样性种群，本文采用传统的部分匹配交叉方式(partially mapped crossed，PMX)，为更大程度地提高种群多样性，直接以父代染色体作为交叉对象。针对高质量种群，本文采用边重组交叉算子和PTL片段交叉算子。

边重组交叉算子是由STARKWEATHER等[18]提出的一种强化父代路径上边之间邻接关系遗传性状的个体交叉方式，具有较好的基因继承特性。文献[7]曾提出一种改进边重组交叉算子并将其用于求解VRPSPD，该算子采用概率方式选择邻接节点，在强化子代遗传性状的同时保证了种群多样性。本文采用该改进边重组交叉算子[7]，以染色体解码后的路径集合为父体产生对应邻接表，依次随机选择染色体中的客户节点，从邻接表中选择其前继节点及(或)后继节点，最终形成新的染色体。

由于两个交叉父体可能相同，本文设计一种PTL片段交叉，使相同序列交叉后得到不同的新序列。不同于直接以染色体交叉的PTL两点交叉[19]，PTL片段交叉以父体分割后的路径集合为交叉对象，随机地选择属于某一路径的客户作为交叉片段，交叉时将所选片段分别置于对方的前面，消去与交叉片段相同的客户节点，形成新的子代个体。具体交叉过程见图2。

图2 PTL片段交叉示意图Fig.2 Schematic diagram of PTL segment crossover

2.6 变异操作

为扩大个体搜索空间并在其附近进行深度探索，算法对染色体执行特殊变异。特殊变异包含两部分内容：去除重插入变异、两点互换变异。特殊变异本质上是对个体进行局域深度搜索，算法中主要用于高质量种群中的精英个体。

去除重插入变异是一种较大程度上的变异。变异时，先将父代染色体解码后的路径集合去除部分客户，然后以Osman最大成本插入准则依次重新插入所去除客户后形成的子代染色体。

两点互换变异以染色体分割后的两条路径为父体，分别随机选择一定数量的节点形成多个节点对；针对各节点对，以Osman最大成本节约插入准则为依据进行交换，最终选择具有最大成本节约值的节点对执行变异并形成子代个体。

2.7 选择操作

分级选择法是一种防止早熟收敛而设计的适应度值比例选择法。精英保留选择法将种群中最优个体保留直接进入下一代，可以有效保证算法寻优性能。算法在两个种群中同时采用精英保留选择法和分级选择法，确保在扩大搜索空间、加快搜索速度的同时提高全局搜索质量。

2.8 自适应策略

遗传算法搜索性能很大程度上受到交叉概率和变异概率的影响，取值过大容易破坏群体中的优良模式；取值过小容易导致产生新个体的能力变差，导致过早收敛。本文采用一种自适应策略调整高质量种群的交叉概率和变异概率，以寻求保护种群优秀性状得以遗传与避免早熟收敛两者之间的平衡，其交叉概率Pc和变异概率Pm分别为[20]

(15)

(16)

2.9 算法整体流程

自适应并行遗传算法试图从搜索空间的广度及深度两个维度进行扩大搜索，通过引入多样性种群和高质量种群的双种群并行策略，并针对高质量种群中的个体进行自适应遗传操作，以进一步提高高质量种群的寻优性能。算法流程框图见图3，详细步骤如下。

图3 自适应并行遗传算法流程图Fig.3 Flowchart of adaptive parallel genetic algorithm

(1)初始化种群参数PS、交叉概率Pc、变异概率Pm、最大迭代次数tmax、全局极值连续未更新最大次数gsn；

(2)采用2.3节的种群初始化方法产生初始种群，种群数目为PS；

(3)将上述初始种群复制两个，分别命名为多样性种群ChromOne和高质量种群ChromTwo；令迭代次数t=0；

(4)如果迭代次数不超过最大迭代次数tmax或连续未更新次数不超过最大次数gsn，执行以下操作：

①针对多样性种群：

a.计算种群的目标函数值、适应度值；

b.采用精英保留策略，将种群中目标函数值最小的个体bestChromOne保存并复制给高质量种群ChromTwo；

c.对种群执行多样性交叉变异操作：PMX交叉和两点互换变异；

d.更新多样性种群，即将原精英个体bestChromOne加入交叉操作后的种群，得到多样性种群子代，此时该种群大小为PS+ 1；

e.计算多样性种群子代的目标函数值、适应度值；

f.采用分级选择法，从新种群中选择PS-1个个体，加上原精英个体bestChromOne，形成新的多样性种群。

②针对高质量种群：

a.计算种群的目标函数值、适应度值；

b.采用精英保留策略，将种群中目标函数值最小的个体bestChromTwo保存；

c.对种群所有个体执行自适应交叉操作：改进边重组交叉或PTL片段交叉；

d.对交叉后的种群所有个体执行自适应两点互换变异操作；

e.对两个种群的原精英个体bestChromOne、bestChromTwo执行特殊变异；

f.将经过步骤e后得到的两个新精英个体加入经过步骤d后得到的种群中，得到高质量种群子代，此时该种群大小为PS+ 1 + 1；

g.计算高质量种群子代的目标函数值及适应度值，找出目标函数值最小的精英个体，更新bestChromTwo；

h.采用分级选择法，从高质量种群子代中选择PS-1个个体，加上精英个体bestChromTwo，最终形成新的高质量种群。

③对于两个种群中的精英个体bestChromOne、bestChromTwo，分别执行特殊变异的后优化操作，如果后优化操作使得该精英个体的目标函数值进一步降低，则更新该精英个体；否则不更新。选择目标函数值较小的精英个体作为全局最优个体。

④t←t+1，转步骤①。

(5)输出全局最优个体及其目标函数值，以及最优路径集合。

3 算例测试与比较

为验证算法寻优性能，选取2个算例进行寻优测试。算法采用MATLAB R2009b编程语言实现，微机运行环境为：CPU i5-2520，主频2.5 GHz，内存4 GB。

3.1 算例选取及参数设置

3.1.1算例选取

选取Augerat标准测试集中24组数据作为算例1，用于验证小规模情况下以总配送距离为目标时算法对模型(式(1))的求解精度。Augerat测试集分为A、B、P三类数据，从客户分布、客户需求量及车容量等方面体现VRPSPD问题的不同要求，对算法求解精度要求较高。算例1中除客户集货需求服从[0，26]的均匀分布[4]外，其余数据均采用文献[21]中的基础数据。

选取NAGY标准测试集中12组数据作为算例2，用于验证大规模情况下，以总配送成本为总目标、以车辆数最少和总配送距离最短为子目标时算法对模型(式(1))的求解精度，同时也用于分析双种群并行策略、种群初始化方法及自适应遗传算子对算法性能的影响。

3.1.2参数设置

试验发现，种群大小PS、最大迭代次数tmax在求解精度及计算耗时等方面对算法整体性能影响较大。为寻求种群大小和最大迭代次数的最佳组合，本文选取7个不同规模问题(客户数为15～199)作为参数试验算例，每个算例以不同参数组合独立运行20次。表1给出不同参数组合情况下本文计算最优值与文献最优值的偏差百分比，表2给出不同参数组合情况下平均计算时间。两表中“均值”一栏是指在同一参数组合下7个算例结果的算术平均值。表1中偏差百分比的计算式为本文最优值与文献最优值之差再除以文献最优值，最优值的取法如下：①当本文所得车辆数与文献车辆数相同时，最优值取为行驶距离；②当本文所得车辆数比文献车辆数小，但行驶距离比文献距离大时，最优值取为车辆数取，否则最优值取为行驶距离；③当本文所得车辆数比文献车辆数大时，最优值取为车辆数。

表1 不同参数组合最优值偏差百分比统计

表2 不同参数组合最优方案计算时间统计

对表1中“均值”数据进行分析发现，在上述9种参数组合情况下，除种群大小为50外的其余6种组合的偏差百分比均为负数，说明本文算法在求解上述7个算例时均能得到比文献算法更好的结果。其中，150/1 000组合的偏差百分比(-11.9%)最小，说明种群数越大、迭代次数越大，计算结果越好，但由表2知其计算消耗的平均时间也最长。因此，通过对表1、表2统计数据进行综合分析，最终选择以较少计算时间产生较好计算结果的150/300为最佳参数组合方式。

以种群PS=150、tmax=300为试验基础，最终确定其他参数为：交叉概率Pc=0.8，变异概率Pm=0.03， 全局极值连续未更新最大次数gsn=100。

3.2 结果分析

3.2.1算例1分析

表3 算例1计算结果比较

以算例1的24组算例为基础数据，采用本文算法进行20次独立仿真计算，得到各算例的最优行驶距离。将计算得到的最优行驶距离与文献[4]采用基于遗传算法的方法(GA based approach，GAA)所得到的最优行驶距离进行比较，对比分析情况见表3。表中加粗字体表示行驶距离最优值。可见，GAA算法在求解A-n38-k5.vrp、A-n39-k5.vrp、B-n39-k5.vrp、P-n23-k8.vrp四个算例时，能取得比本文算法更优的行驶距离。而本文算法在24组算例中，除4个算例的最优行驶距离大于GAA算法的结果外，其余20组算例均得到更好的近似最优解。在这20组算例中，除算例A-n45-k6.vrp的行驶距离与GAA算法结果相同外，其余19组算例的决策结果均优于GAA算法。

本文进一步采用t-test显著性差异检验法验证所提算法的优越性。首先采用KS-test检验数据的正态分布特性，进行如下KS-test检验假设：

H0表示两种算法结果服从正态分布；

Ha表示两种算法结果不服从正态分布。

设置置信度为95%，采用SPSS软件进行“单样本K-S(1)”检验分析，结果见表4。由于表中两种算法结果数据的双侧显著性取值均大于0.05，因此否定H0假设并接受Ha假设，即认为两种算法结果均服从正态分布，可以采用t-test进行显著性差异验证。

表4 KS-test检验统计分析结果

进行t-test前，进行如下检验假设：

H0表示两种算法结果的均值差等于0；

Ha表示两种算法结果的均值差不等于0。

设置置信度为95%，采用SPSS软件进行“比较平均值-成对样本T检验”，得到Sig(双尾)=0.001<0.05。可以看出拒绝H0假设的概率只有0.1%，故接受Ha假设，即认为两种算法结果均值不相等。但这仍然不能证明本文算法结果的均值小于GAA算法结果的均值，因此，需要做进一步的单侧t-test检验。重新做出如下假设：

H0表示本文算法结果均值-GAA算法结果均值等于-15；

Ha表示本文算法结果均值-GAA算法结果均值小于-15。

设置置信度为95%，采用SPSS软件进行“比较平均值-成对样本T检验”，得到Sig(单尾)=0.006<0.05。可以看出拒绝新H0假设的概率只有0.6%，因此，接受新Ha假设，即认为本文算法结果的均值小于GAA算法结果均值。

由此可以推断，本文算法在求解VRPSPD时具有更好的寻优能力。此外，由表3中计算时间来看，本文算法在大部分算例运算时消耗时间更少，证明本文算法具有更高的计算效率。

3.2.2算例2分析

以算例2的12组算例为基础数据，采用本文算法进行20次独立仿真计算，将所得最优值与文献[5]的启发式算法、文献[9]的禁忌搜索算法、及文献[10]的自适应禁忌搜索算法所得最优值进行比较，分析结果见表5，表中加粗字体表示对应算例的最优值。显然，文献[10]的自适应禁忌搜索算法比其他两种算法效果更好。然而，与自适应禁忌搜索算法[10]相比，除了CMT7X、CMT7Y、CMT9Y、CMT13X四个算例外，本文算法在求解其余8组算例时均能取得更好的行驶距离，其偏差百分比最大达到-21.3%。此外，本文算法还对6组算例的车辆数目进行了改进，其偏差百分比最大达到-30%。

表5 算例2计算结果比较

由于CMT13X、CMT14Y问题部分节点呈随机分布、部分节点呈丛聚式分布，且具有车辆最大行程及节点装卸时间限制的诸多特征，使得它们的求解较其余10组问题更为困难。针对这两个问题，尽管行驶距离比自适应禁忌搜索算法大一些，但使用车辆数较之少1辆。由于车辆指派成本为一个很大的正整数，故车辆数目的减少可以大大降低总配送成本。由此可以推断，本文算法在求解带指派成本的VRPSPD时具有更好的优化性能。

3.2.3算法性能分析

为进一步分析双种群并行策略、种群初始化方法及自适应交叉变异操作对算法性能的影响，选取算例2中CMT8X作为对比分析对象，以种群大小为150、最大迭代次数为300、交叉概率为0.8、变异概率为0.03的组合参数，独立运算20次，选取最优近似解进行分析。

采用双种群并行策略与采用单一种群时的对比情况见图4。选取两种单一种群方式与双种群并行策略进行对比：一种为舍弃多样性种群、保留高质量种群的单一种群方式，另一种为包含小部分高质量个体、大部分多样性个体的单一种群方式，图4中分别采用ONE_POP_HQ、ONE_POP_DR_HQ表示，双种群并行策略采用TWO_POP_PARALLEL表示。由图4可见，单纯采用高质量种群可以获取比较好的初始解，但在搜索过程中由于搜索空间变小很容易陷入局部最优；包含部分高质量个体、大部分多样性个体的单一种群方式虽然扩大了搜索空间，在一定程度上改善了种群多样性，但仍然无法跳出局部最优。而双种群并行策略却能以较少的迭代次数取得更小的行驶距离，说明本文提出的双种群并行策略在遗传算法求解VRPSPD问题时，不仅能有效帮助算法在有限迭代次数内进行广度与深度的同步探索，而且能有效避免陷入局部最优，最终以较短时间快速寻找到近似最优解。

图4 ARALLEL与NO_PARALLEL收敛性对比Fig.4 Comparison of convergence between ARALLEL and NO_PARALLEL

采用2.3节的种群初始化方法与不采用该方法时的对比情况见图5。图例INITIAL_PDCW、INITIAL_PDMPCW、INITIAL_PDMPRCW分别表示单独采用2.3.1节、2.3.2节和2.3.3节中的初始化方法，图例INITIAL表示同时采用上述三种初始化方法。图例NO_INITIAL表示不采用上述初始化种群方法，而以任意产生PS条大路径序列方式对种群进行初始化。可见，在INITIAL情况下初始行驶距离较INITIAL_PDCW、NO_INITIAL要小很多，但比INITIAL_PDMPCW、INITIAL_PDMPRCW要大一些，这说明，针对具有双重需求的VRPSPD问题，其初始解质量在单纯考虑客户需求量对插入节点节约值的影响时最差，在增加考虑不同节点之间运输费率或运输距离对节约值权重影响、且不固定客户节点时最好，而同时考虑3种初始化方法仅处于中间状态。但是，同时考虑3种初始化方法在中后期收敛效果好，行驶距离更小，这说明初始化种群方法对本文算法求解VRPSPD问题的性能具有较大影响，良好的种群初始化方法能促使其收敛加快并保持良好寻优能力。

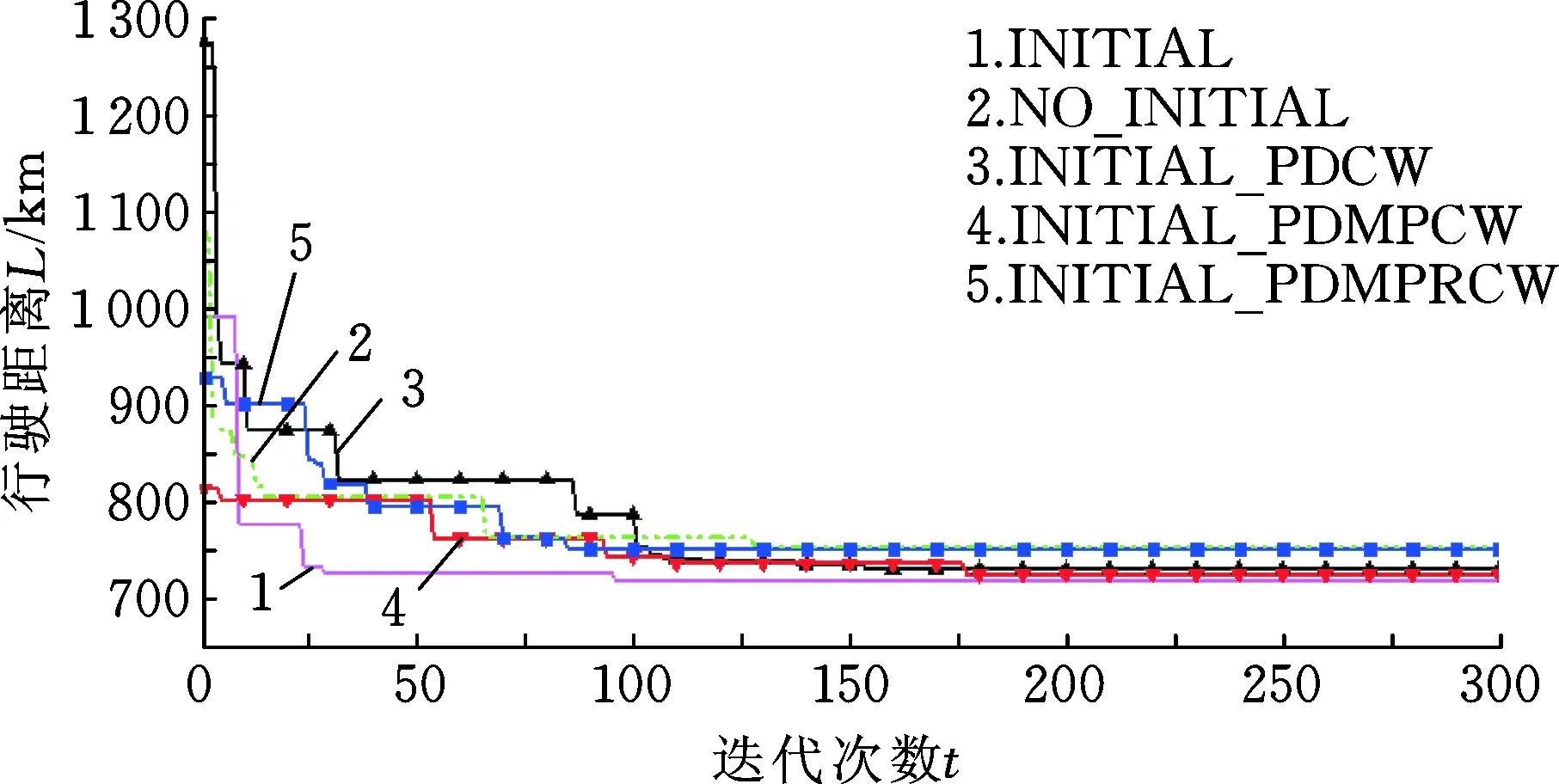
图5 INITIAL与NO_INITIAL收敛性对比Fig.5 Comparison of convergence between INITIAL and NO_INITIAL

采用自适应交叉变异操作与交叉变异概率均恒定不变的对比情况见图6，图例分别为ADAPTION、NO_ADAPTION。由图可见，当交叉变异概率恒定不变时，算法收敛速度慢，容易在阶段性收敛后产生停滞从而陷入局部最优；而采用适应性变动的交叉变异操作能加快收敛速度，提升收敛效果，以较少的迭代次数搜索到更短的行驶距离。这说明本文提出的自适应交叉变异操作在遗传算法求解VRPSPD问题时，能提高进化早期的全局搜索能力以及进化后期的局部搜索能力，有效提高搜索质量。

图6 ADAPTION与NO_ADAPTION收敛性对比Fig.6 Comparison of convergence between ADAPTION and NO_ADAPTION

4 结论

装卸一体化车辆路径问题是一类具有双重需求特征的复杂车辆路径问题，因其决策目标、决策因素和限制条件较多等特征需要高求解性能的启发式方法或元启发算法。针对装卸一体化车辆路径问题，本文建立了以总配送成本为优化目标的混合整数规划模型，提出了求解装卸一体化车辆路径问题的自适应并行遗传算法。该算法采用3种基于C-W的改进启发式算法产生初始种群，并引入多样性种群和高质量种群的双种群并行策略，同时采用保留精英及随着进化过程适应性改变交叉变异概率的自适应遗传操作，实现搜索空间在广度和深度上的同步拓展。针对不同规模、不同总目标，分别基于两个算例进行仿真分析。仿真结果表明，无论是单纯以总行驶距离为目标的算例1问题，还是以总配送成本为总目标、以车辆数最少和总行驶距离最短为子目标的算例2问题，本文提出的自适应并行遗传算法都能以较快的收敛速度找到近似最优解，且寻优性能强于已有的基于遗传算法的方法、插入式启发式算法、禁忌搜索算法以及自适应禁忌搜索算法。由此可见，本文所提算法对具有较大车辆指派成本的物流配送和取货优化问题具有重要的指导意义，同时对离散型组合优化问题的进一步研究也具有一定的理论参考价值。