一种求解单机总加权延迟调度问题的改进蚁群算法
2018-12-11乔东平文笑雨肖艳秋焦建强
乔东平 裴 杰 文笑雨 肖艳秋 焦建强
1. 郑州轻工业学院机电工程学院,郑州,450002 2.河南省机械装备智能制造重点实验室,郑州,450002
0 引言
单机总加权延迟调度(single machine total weighted tardiness scheduling, SMTWTS)问题是考虑作业完工时间满足预定交货期,优化目标为最小化加权延迟成本的单机调度问题。LAWLER[1]证明了SMTWTS问题为NP-Hard问题。随着求解规模的扩大,该类问题求解复杂度及求解时间呈现指数级增长。针对该问题设计有效的调度算法,一直是生产调度领域的重要研究课题之一。目前,对该类问题已提出一系列有效的求解方法。依照优化机制和优化行为的不同,解决SMTWTS问题的算法可分为精确算法、基于优先分配规则的构造性启发式方法和元启发式算法[2]。BABU等[3]构建的分支定界算法解决了50个作业规模的基准问题;YIN等[4]结合候选作业特征提出一种新的构造性启发式规则(mixed dispatch rule, MDR),以更有效地求解SMTWTS问题;YAHYAOUI等[5]、FU等[6]研究了求解SMTWTS问题的变邻域搜索(variable neighborhood search,VNS)算法;SUPPIAH等[7]、UMI等[8]分别采用遗传算法和禁忌搜索算法(TS)对SMTWTS问题作了进一步探讨;MADUREIRA等[9]、叶强等[10]针对OR-Library中的多个基准问题,研究分析了蚁群算法对SMTWTS问题求解的有效性。
分支定界、动态规划等精确算法虽能在一定条件下产生最优解决方案,但受限于计算复杂性,仅能有效解决较小规模的实例问题。基于优先分配规则的构造性启发式方法为求解单机调度问题提供了一种快速排序方法,但算法求解质量依赖于调度规则的选取。以模拟自然现象及规律而发展的元启发式算法更易在合理时间内以较大概率求得问题的满意解,为复杂调度问题的研究提供了新的思路和手段,成为目前求解调度问题的主要方法。
蚁群优化(ant colony optimization,ACO)算法[11]已在作业车间调度[12]、路径规划[13]等优化领域中得到广泛应用。鉴于该算法的诸多优良特性,本文针对SMTWTS问题特点,提出一种基于信息素差异更新的改进蚁群优化 (improved ant colony optimization,IACO)算法以更有效地求解SMTWTS问题。首先,该算法采用确定性选择与随机性选择相结合的策略,结合MDD优先规则改进了启发式信息的设定。其次,通过引入正负反馈机制,提出一种改进的差异化信息素更新策略,并结合局部优化策略实现了对调度序列的进一步优化。最后,OR-Library中多个不同规模基准算例的仿真验证了算法具有较好的寻优性能。
1 SMTWTS问题描述
单机总加权延迟调度问题1‖ΣwjTj可描述如下:n个相互独立的作业安排在1台机器上完成,机器连续处理且同一时刻最多只能完成1个作业任务,各作业均可在0时刻到达并加工,作业间的加工顺序不预先设定。第j(j=1,2,…,n)个作业有3项独立参数:加工时间pj、权重即延迟惩罚系数wj及交货期dj,各作业参数与其在加工序列中的位置无关。
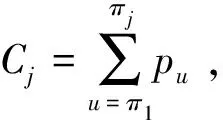
(1)
求解中,对该调度模型作如下假设:①各作业无准备时间,在0时刻,所有作业均可被处理;②作业的处理时间、交货日期和权重在计划开始时均为已知且确定;③不同作业具有相同的优先级,其加工顺序不预先设定;④工件在机器上仅加工一次,且机器一次只能处理一个作业;⑤机器进行连续加工,不允许抢占和中断;⑥当前作业完成后,下一个计划作业立即开始执行。
2 求解SMTWTS问题的改进蚁群算法
2.1 描述SMTWTS问题的变量定义
在IACO算法中,每个蚂蚁通过对作业节点的逐步选取,最终构建出完整的作业序列。解决方案的构建过程受启发式信息和信息素指导,初始信息素及启发式信息分别结合最早交货期(earliest due date, EDD)优先规则和修正的MDD启发式规则给出。每次迭代中,当所有蚂蚁都构建出完整的解决方案后,采用改进的差异化信息素更新规则对构成该可行解的各节点间的信息素做更新处理,然后引入局部搜索以改进每次迭代搜索到的最佳解决方案。IACO算法的相关变量定义如下:(i,j)表示在位置i处理作业j;α为信息素对蚂蚁选择路径的影响力,α≥ 0;β表示启发信息值的相对重要性,β≥ 0;ρ为信息素挥发因子,ρ∈(0, 1);NC为迭代计数器变量;NCmax为算法最大迭代次数;S*为当前最优调度序列;T*为当前最优调度序列的总加权延迟成本。
IACO算法的求解流程可描述如下:
Procedure单机调度问题的改进蚁群算法
参数设置;
结合EDD优先规则初始化各节点间信息素;
While不满足终止条件 do
For 蚂蚁k=1 tom
For 加工序列位置i=1 ton
按选取规则构造可行解;
End for
End for
差异化信息素更新规则更新节点间信息素;
Application局部搜索策略;
If 搜索到当前最优解决方案π的改进解π*
then
Setπ←π*andTπ←Tπ*
更新解决方案π相关节点间信息素;
End if
End while
Return最优调度序列S*and该方案下的总加权延迟成本T;
End Procedure
2.2 编码方式
基于问题特性的编码方式能更好地提高算法的优化性能。对于本文研究的1‖ΣwjTj问题,采用基于作业序列的构建性编码方式:初始时刻,m只蚂蚁随机选取作业j安排在加工序列的起始位置进行处理;其次,按照2.4节中定义的多样性选取规则逐步将尚未安排的作业添加到加工序列的后续位置,直至完成所有作业调度。编码后得到一个完整的作业处理序列。表1给出了作业处理序列为J1-J7-J3-J2-J5-J6-J4,总加权延迟成本T=30的一个解决方案示例。
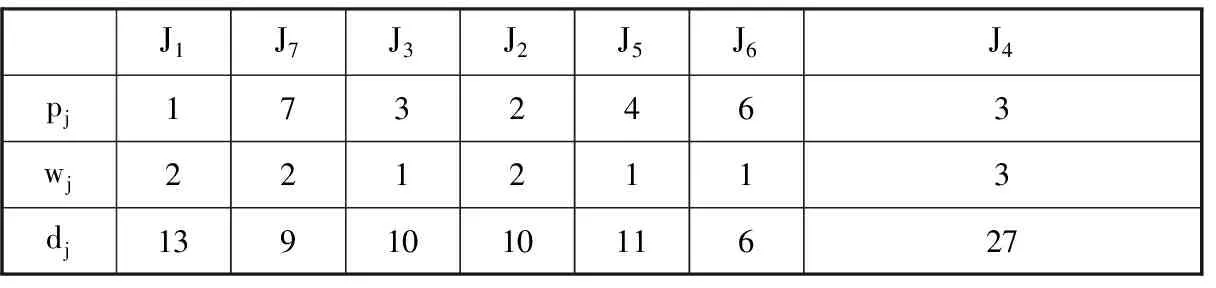
表1 基于作业序列的编码
2.3 初始化
2.3.1初始化参数设置
令NC=0, 设置最大迭代次数NCmax,初始化当前最优调度序列π*为空集,当前最优调度序列的总加权延迟成本T*为无限大。
2.3.2初始化信息素
在所提出的改进蚁群算法中,τij为任意时刻节点(i,j)间的信息素浓度。初始信息素浓度τij(0)的设定影响算法状态转移概率的计算,对蚂蚁后续的搜索产生影响。若信息素释放量远大于信息素初始值,则在正反馈机制的作用下,算法将很快集中搜索于蚂蚁最初生成的几条路径,导致搜索陷入较差的局部空间;反之,算法则需要较多次的初期迭代才能有效反映出不同节点的优劣性,从而正确指导蚂蚁开始有偏向性地进行搜索。因此,为使算法具有较好的搜索性能,信息素初始值应略大于每次迭代中蚂蚁释放的信息素期望值。
考虑到蚂蚁的信息素释放量多设定为1/Trnd(Trnd为蚂蚁搜索到的任一调度序列的加权延迟目标值),算法在初始时,按τij(0)=n/TEDD分配节点(i,j)间的初始信息素,其中,TEDD为采用最早交货时间序列规则生成的作业序列下系统的总加权延迟成本。
2.4 调度序列构建
当IACO算法用于求解SMTWTS问题时,每次迭代中,m只蚂蚁独立构造一个可行调度方案。SMTWTS问题的一个可行解决方案为n个作业排列组成的处理序列。在可行调度方案的构建过程中,每只蚂蚁从一个空序列开始,通过选取规则逐步将一个未调度的作业j添加到已构建的部分序列中,最终构建出一个完整调度方案。将作业j添加到部分序列的决策是按照蚁群算法的状态转移规则进行的,这个过程受节点间信息素τij及任意时刻节点(i,j)间的启发信息值ηij的共同影响。
状态转移规则的设定对蚁群算法的优化性能具有重要影响:若不同作业间的状态选取概率差异过大,则易使算法过早陷入局部最优状态;反之,则导致算法难以有效利用迭代过程积累的搜索经验,收敛性能较差。
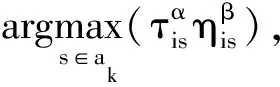
(2)
计算各可选作业在该位置处的加工概率,然后结合轮盘赌规则选出待加工作业。
采用确定性选择与随机性选择相结合的选择策略。通过对q0的调整,可以调节算法对当前较优解区域及其他未知解空间的探索度,有利于提高解空间的多样性,避免算法过早陷入局部最优。
2.5 启发式信息的设定
启发式信息的设定反映了优化问题的成本代价或成本代价的估计值。对ηij的有效设定直接影响到算法的求解效率及全局收敛性。在本文所述SMTWTS问题中,启发式信息ηij表征作业j安排在位置(作业处理序号)i(i=1,2,…,n])进行加工的期望程度。针对该问题,文献[10]采用基于MDD的优先规则定义ηij:
(3)
式中,Cj-1为已安排作业的总加工时间。
若待选作业j在加工位置i能早于其交货期dj完成加工,则具有较早交货期的作业被选择在位置i加工的概率就大。此外,对于迟于交货期完成的候选作业,处理时间较短的作业拥有更高的加工优先级。
式(4)对于启发式信息的定义仍存在部分不足:由于大部分基准实例问题的交货期dj通常较大,尤其在求解大规模实例问题的调度决策后期,加工时间的累积将使max(Cj-1+pj,dj)的取值变得很大,因此,这些作业间的启发式信息差异通常较小。这意味着启发式信息可能无法完全正确反映出其对蚂蚁决策的相对影响。
为了减弱上述影响,提出采用由下式定义的启发式信息:
(4)
式中,wj为待选作业j的权重。
若Cj-1+pj≥dj,则具有较小加权处理时间pj/wj的作业具有较大的启发式信息值。
2.6 信息素更新
在所有蚂蚁完成一次完整遍历后,对构成该可行解的各节点间的残留信息做更新处理。为使算法在对较优节点信息充分利用的同时,也保持较好的全局搜索能力,避免过早陷入局部最优,提出一种改进的差异化信息素更新策略,对各节点间信息素进行全局更新处理。
在所述差异化信息素更新规则中,根据蚂蚁构建的方案质量,引入正负反馈机制对各节点间信息素进行自适应差异化更新,使当前最优节点的变化能迅速表现在节点间的信息素分布上。该过程受迭代最优调度方案的总加权延迟成本Tib、迭代最差调度方案的总加权延迟成本Tworst及所有调度排序方案的平均延迟成本Tave的影响。改进的信息素更新策略描述如下:
(5)
式中,ρ为信息素挥发系数;Tk为本次迭代中蚂蚁k搜索到的排序方案下的总加权延迟成本;Δτijk为蚂蚁k在本次循环中留在节点(i,j)间的信息素量;Δτij为本次循环中节点(i,j)间的信息素增量和。

(6)
式中,Q为预先设定的总信息量。
式(5)、式(6)根据蚂蚁构建的调度方案质量动态调整各节点间的信息素。对于目标值小于迭代平均延迟成本的较优调度排序方案,延迟成本越小,其所含节点间信息素增量越大,节点间就会获得更多的信息素,在后续迭代中就可能会被更多的蚂蚁所选择;对于目标值大于迭代平均延迟成本的较差调度排序方案,延迟成本越大,该方案所含节点间信息素减少的越多。相较于基本蚁群算法,该改进通过对不同质量调度排序方案进行信息素差异化更新,增大较优节点对蚂蚁的吸引力,降低较差节点对蚂蚁选择的干扰,使得算法快速向全局最优调度序列的方向搜索。
2.7 局部搜索策略的应用
为进一步改善调度方案质量,对所有蚂蚁每次迭代搜索后产生的迭代最优方案引入局部搜索策略。局部搜索策略基于对候选解π的邻域进行迭代探测,通过局部调整当前解决方案中的部分作业序列来提高调度方案质量。在本文中,采用成对交换策略以进一步实现解序列的优化改进。
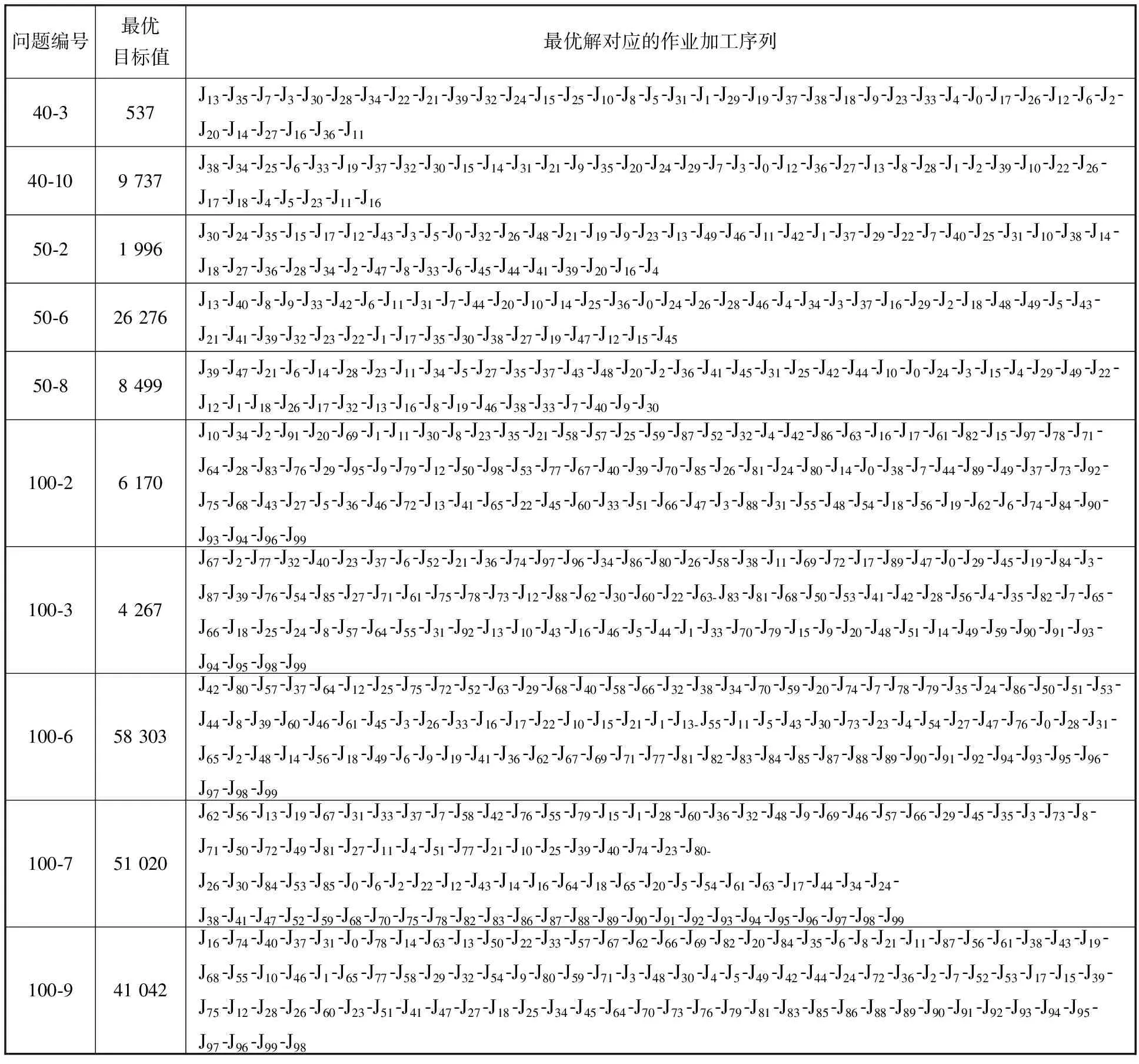
成对交换策略中,候选解π的交换邻域是在满足i2-i1≤r(i2>i1;r为可调参数,r=1,2,…,n-1)的条件下,通过交换π中i1和i2位置的作业而得到的所有候选解π*的集合。成对交换是梯度下降的,它只接受可降低系统总加权延迟成本的可行调度方案。若在当前候选解的邻域内找到更好的调度序列π*的加权延迟目标值满足Tπ* 考虑到有着临近交货期的作业必定在相近时刻先后安排加工才能保证整体最优,因此,通过调整具有相近交货期的部分作业序列可进一步改善方案质量。以r=4为例(任一作业与其紧邻的4个作业依次交换)的成对交换策略执行伪代码可描述如下: Procedure成对交换 对于任一迭代最优作业序列π Forr=1 to 4 Fori1=1 ton-r Fori2=i1+r Exchange [i1][i2]位置上的作业生成新的作业序列π*; Ifπ*优于当前最优解决方案πthen π←π*,Tπ=Tπ* 更新解决方案π相关节点间信息素; End if End for End for End for End Procedure 按照上述交换步骤,以表1为起始解决方案的一个成对交换局部优化示例如图1所示。 图1 局部优化示例Fig.1 Local optimization example 通过对迭代最优方案引入局部优化策略,将全局搜索与局部搜索有机结合,以较小的运算代价有效改善了调度方案质量,提高算法优化性能。且上述交换策略只考虑了有限数量的交换邻域,相比于文献[14]的全局迭代交换,该方法更加简单有效。 为验证IACO算法对SMTWTS问题的求解性能,实验选用OR-Library[15]中问题规模n分别为40、50、100的各10个基准问题进行测试,并与蚁群算法及遗传算法(GA)进行求解比较。为使所选实例问题更具有一般性,30个实例问题均来自不同规模基准问题集的前10项。 3种算法均采用Java语言编程,并在内存为8 G,Intel Core i7-3770 CPU的PC上进行测试。分别对每个实例问题进行20次独立实验,每次进行2 000次迭代,ACO算法和GA算法的其他参数分别设置为文献[16-17]中给出的建议值,IACO算法参数结合实验测试并设置如表2所示。 表2 IACO算法参数设置 表3统计了3种算法对不同基准问题的实验结果。表3中,Tknow为已知最佳解决方案的总加权延迟目标值,Tbest为算法搜索到的最佳结果,Tmean为算法20次求解的平均值,Hr为20次实验中搜索到已知最佳解决方案的命中率,偏差dev为算法搜索到的最优解Tbest与已知最优解Tknow的偏离程度: (7) 表3 不同实例问题的求解结果 (续表) 基准算例基本蚁群算法ACO遗传算法GA改进蚁群算法IACOn编号TknowTbestTmeanHr(%)dev(%)TbestTmeanHr(%)dev(%)TbestTmeanHr(%)dev(%)10015 9886 0406 24300.875 9886 286.5505 9886 054.440026 1706 2466 47201.236 2006 408.100.496 1706 288.530034 2674 3074 476.800.944 2804 482.800.304 2674 312.6510045 0115 0555 252.500.885 0115 235.5505 0115 151.5515055 2835 2885 515.800.095 2835 523.3505 2835 402.95550658 25861 54965 458.805.6559 13660 696.301.5158 30359 542.400.08750 97252 79955 207.803.5851 94353 263.201.9051 02055 152.900.09859 43460 99163 677.602.6260 58461 840.101.9359 55960 968.800.21940 97842 75144 437.604.3342 25343 23703.1141 04242 993.300.161053 20854 82156 833.803.0354 82155 890.803.0353 34254 842.300.25 表4给出了表3中部分实例问题求得的最优解所对应的具体加工序列。 表4 部分实例问题最优解对应的加工序列 由表3可知,对于SMTWT问题规模为n=40,50的多个基准算例,IACO算法和GA均能在实验设定条件下获得问题的最优目标值,ACO算法的求解结果稍差于IACO算法和GA,仅取得了少数最优值。从其他统计参数来看,IACO算法的搜索成功率和平均求解结果等指标多优于GA且均明显好于ACO算法,对每个基准问题的平均求解结果与最优解也极为接近,表明改进算法对该类规模SMTWTS问题具有较好的求解性能及求解稳定性。 对于表3中n=100规模的后4个基准问题,3种算法均未能在算法停止时搜索到最优解。由实验统计结果可知,IACO算法的误差率均在0.3%内,明显优于其他2种算法,表明IACO算法在相同的迭代停止条件下具有更好的全局收敛性。 实验同时给出针对n=40,50,100三种不同规模基准实例问题中编号为5的算法收敛曲线,如图2所示。 图2 实例问题5的算法收敛曲线图Fig.2 Algorithm convergence curve for instance cases 5 图2中,3种算法均以1000次迭代为停止条件。由图2可知,GA的收敛过程“阶段性”特征较为明显,收敛较慢;ACO算法能快速收敛,但两种算法对n=50,100规模的两个实例问题均未能在指定停止条件下得到问题的最优解。IACO算法能在更少迭代次数内快速收敛到最优解附近并趋于稳定,图2所示的3个实例均能在300次迭代内获得问题的最优解,表明改进算法具有较强的搜索能力。 综合上述实验分析可知,对于多数基准算例,IACO算法在求解质量、收敛稳定性等方面均显著优于GA及ACO算法,其原因如下:①多样性节点选取规则和差异化信息素更新策略的应用,使得算法在对较优节点搜索经验更好利用的同时,提高了解空间的多样性和算法的搜索能力。②改进的启发式信息简洁,准确描述了作业在加工序列中不同位置的加工关系,信息素的正反馈更新机制强化了较优调度节点被选取的概率,保证了算法快速向最优调度序列的方向搜索。③局部搜索策略的引入,弥补了ACO算法局部搜索能力差的不足,在一定程度上降低了算法过早陷入局部最优的概率。 本文针对单机总加权延迟调度问题,提出一种基于信息素差异化更新的改进蚁群调度算法。该算法采用确定性选择与随机性选择相结合的选取规则,结合MDD调度规则改进了启发式信息函数,实现了SMTWTS问题的调度序列构建;引入正负反馈机制对各节点间信息素进行自适应差异化更新,提高了解空间的多样性,避免了算法的过早停滞。同时结合局部优化策略实现了对可行调度方案的进一步优化。OR-Library中多个基准实例的仿真实验表明,该改进算法对SMTWTS问题具有良好的优化性能。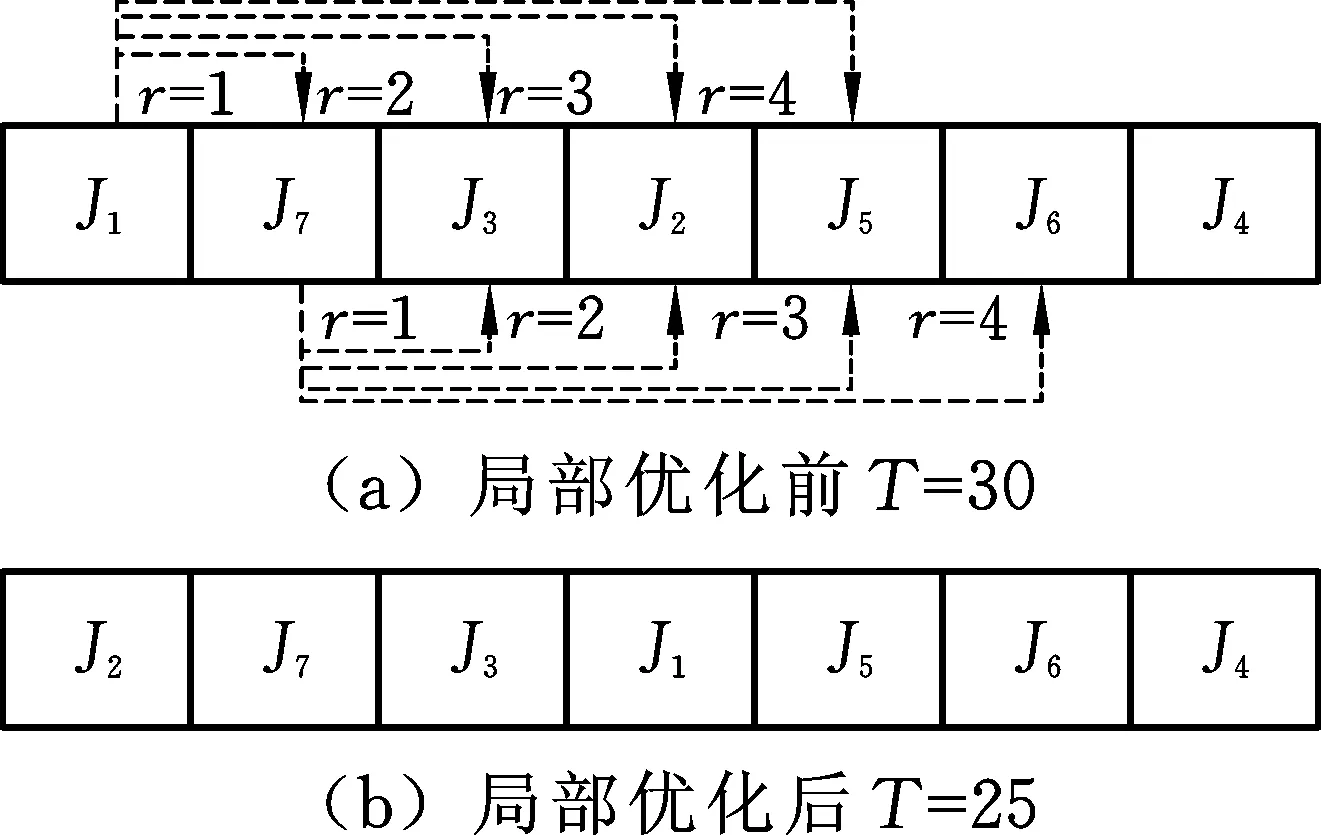
3 实验分析




4 结语
