混合布谷鸟算法求解绿色流水车间调度问题
2018-12-11钟祾充
钟祾充 钱 斌 胡 蓉 王 凌
1.昆明理工大学信息工程与自动化学院,昆明,650500 2.清华大学自动化系,北京,100084
0 引言
全球变暖是由温室气体的过度排放引起的,特别是二氧化碳(CO2)的过度排放。其中,化石燃料的燃烧成为CO2排放的主要原因。合理减排能够减缓地球变暖。本文研究的问题模型包含环境指标,符合当前生态环境治理的需求。根据FANG等[1]的调查,约一半的世界能源消耗来自工业部门,制造企业已经成为全球变暖的主要因素之一。一方面,法律法规对温室气体的排放量控制使得制造企业不得不限制碳排放;另一方面,高碳排放量带来的高税收也使得制造企业寻求切实可行的方法来减少能源消耗。
在传统生产调度问题上,主要考虑的优化指标或目标均与时间、成本和质量相关。当制造业面对日益增强的环境和节能压力时,便需要在生产制造过程中协同考虑经济指标和绿色指标。本文所研究的带绿色指标的多目标置换流水线生产调度问题(multi-objective permutation flow shop problem,MOPFSP)具有较强的工业背景。在计算复杂度上,2台机器以上的置换流水车间调度问题(permutation flow shop scheduling problem,PFSP)被证明是NP-hard问题[2],因此,更为复杂的MOPFSP也属于NP-hard问题。综上,开展带绿色指标的MOPFSP求解具有重要的工程和学术意义。
在过去几十年里,流水线车间调度问题已被广泛研究,然而,近十年来才有一些文献同时考虑经济和环境指标。LUO等[3]针对带电力消耗的多目标混合流水车间调度问题,设计了蚁群优化算法进行求解。DING等[4]针对带碳排放总量的多目标流水车间调度问题进行研究,并提出了一种改进的迭代贪心算法求解该问题。LIU等[5]设计了一种自适应多目标遗传算法,可有效求解一类带碳排放和总加权延迟两个优化指标的流水线车间调度问题。DING等[6]提出了基于非支配解结构特性的迭代贪心算法,用于求解带碳排放总量的双目标流水车间调度问题。TANG等[7]提出了改进的粒子群优化算法,可求解基于能源消耗和最长完工时间两个目标的柔性流水车间调度问题。LU等[8]针对带能源消耗的多目标流水车间调度问题,提出了一种基于机器设置时间和工件运输时间的混合多目标回溯搜索算法进行求解。综上所述,带绿色指标的多目标流水车间调度问题的研究仍较为有限,迫切需要加强对求解该类重要问题的有效方法的研究。
布谷鸟搜索 (cuckoo search,CS)算法是YANG和DEB于2009年提出的一种元启发式算法,该算法根据布谷鸟产卵时的飞行机制进行搜索,能够快速有效地求解连续优化问题。近年来,CS算法也被扩展用于求解带经济指标的单目标生产调度问题。LI等[9]利用NEH启发式规则产生部分初始种群,并设计了一种带局部搜索的混合CS算法对单目标PFSP问题进行求解。MAEICHELVAM等[10]在CS算法的初始阶段采用NEH规则初始化部分种群,进而将其用于求解单目标多阶段混合流水线车间调度问题。ALAA等[11]对CS算法中的莱维飞行公式进行改进,同时加强了对种群最优个体邻域的搜索,并将所提算法用于求解单目标柔性作业车间调度问题。WANG等[12]采用NEH规则产生部分初始种群,继而提出了一种带局部搜索的混合布谷鸟算法,用于求解单目标流水线车间调度问题。由上述文献可知,尚无利用CS算法求解带绿色指标的MOPFSP的相关研究。此外,上述文献均将步长控制因子设定为某个常数,并未对其进行动态调整。实际上,随着算法迭代次数的增加,若步长控制因子设置过大,布谷鸟算法的搜索易偏离优质解区域,从而导致性能变差;若步长控制因子设置过小,该算法在前期就容易陷入局部最优而早熟。因此,针对绿色流水车间调度问题,设计可动态调整步长控制因子的布谷鸟算法进行有效求解,具有重要意义。
本文提出了一种混合布谷鸟(HCS)算法用于求解优化目标为最长完工时间和总碳排放量的MOPFSP。在HCS算法中,不仅提出了一种步长控制因子的自适应调整策略,使布谷鸟算法具有较快的收敛速度和较好的全局搜索性能;同时还设计了一种多邻域局部搜索机制,可对HCS算法全局搜索得到的优质解区域进行细致搜索,进而使算法在全局和局部搜索之间到达较好平衡。最后,通过仿真实验和算法对比来验证HCS算法的有效性。
1 低碳MOPFSP描述
设有n个工件需要在m台机器上加工,每个机器有s种不同的加工速度,其中工件集合为J={1,2,…,n},机器集合为M={1,2,…,m},速度集合为S={v1,v2,…,vs}。Pi,k表示工件i在机器k上的标准加工时间;Vi,k表示工件i在机器k上的加工速度;Pi,k/Vi,k表示工件i在机器k上以速度Vi,k加工时的真实加工时间;Qk,v表示机器k以速度v工作时的单位能耗;Qk表示机器k待机状态时的单位能耗;当t时刻机器k以速度v工作时xkv(t)=1,其他时刻xkv(t)=0;t时刻机器k呈现待机状态yk(t)=1,其他时刻yk(t)=0;π=(j1,j2,…,jn)为所有工件的某种排序;Π是不同排序π的集合;C(ji,k)i=(1,2,…,n)为工件ji在机器k上的完成时间。
PFSP的2个加工规则:①当工件i∈J在机器(k-1)∈M上加工完成之后,工件j∈J才能在机器k∈M上加工。②每台机器每次只能加工一个工件,不能同时加工多个工件。
假设工件j1至jn依次在机器1至机器m上顺序加工,最长完工时间make-span的数学模型如下:
C(j1,1)=Pj1,1/Vj1,1
(1)
C(ji,1)=C(ji-1,1)+Pji,1/Vj1,1
(2)
C(j1,k)=C(j1,k-1)+Pj1,k/Vj1,k
(3)
(4)
Cmax=C(jn,m)
(5)
其中,k=2,3,…,m,i=2,3,…,n;式(5)为最长完工时间。
假设ε是每单位能耗的CO2排放量,CO2排放总量计算公式为
(6)
其中,CT表示能源总消耗;CCO2表示CO2排放总量,以下简称碳排放总量(total carbon emissions,TCE)。
为了计算碳排放总量,需要构建机器的速率矩阵An×m,其中Ai,k∈{1,2,…,s}。假设s=3,Ai,k∈{1,2,3},n=3,m=2,则矩阵A3×2的其中一种情况表示如下:
(7)
如,A31表示第3个工件在第1台机器上的加工速度为3。
对于低碳多目标PFSP,不可能同时求得最长完工时间(make-span)和TCE的全局最优解,但是可以求得这样一组解:任何一个目标的继续优化都必须牺牲其他目标函数值的有效解[13-14]。这类有效解组成的集合称之为非劣解,即Pareto解集。
2 多目标问题相关概念
本文中MOPFSP可以表示为
minF(π)=[f1(π),f2(π)],π∈ψ
(8)
f1=Cmax
(9)
f2=CCO2
(10)
式中,ψ为可行域。
(1)支配。对于目标向量F(π1)=(f1(π1),f2(π1))和F(π2)=(f1(π2),f2(π2)),当且仅当(∀i∈{1,2}:fi(π1)≤fi(π2))∩(∃i∈{1,2}:fi(π1) (2)Pareto优解。对于π∈ψ,当且仅当不存在π′∈ψ使F(π′)F(π)时,称π为Pareto优解。 (3)Pareto解集合。对于Pareto解集合P: P={π∈ψ|π′∈ψ:F(π′)F(π)} (4)Pareto前沿。 对于Pareto前沿PF,有 PF={F(π)=(f1(π),f2(π))|π∈P} YANG等[15]根据布谷鸟寻窝产蛋的行为和莱维飞行(Lévy flight)特征,提出了标准的多目标布谷鸟算法。布谷鸟算法中个体更新方式有两种,第一种是使用莱维飞行公式: xi,t+1=xi,t+α⊕Lévy(λ) (11) 其中,xi,t+1、xi,t分别表示第i个个体在第k代和第k+1代时的位置向量;⊕表示点乘;α为控制步长的步长因子,大多数情况下,α=O(1);Lévy(λ)为莱维飞行搜索路径。 从式(11)可以看出,该分布使布谷鸟的连续位置形成了一种带重尾的概率分布,能扩大搜索范围,增加种群多样性,且容易跳出局部最优。 第二种更新方式是根据一个固定的发现概率Pa与一个随机数β之间的关系确定是否产生新个体,更新公式如下: xi,t+1=xi,t+γH(Pa-β)⊕[xo,t-xk,t] (12) 其中,γ和β二者均服从均匀分布,γ、β∈U[0,1];xi,t、xo,t、xk,t分别为第t代中3个不同的随机个体;H为赫威赛德函数,其计算公式为 (13) 3.2.1自适应步长因子 CS算法虽然在诸多领域得到应用研究,但其本身存在固有不足:莱维飞行是一种马尔科夫链,只与当前情况有关,随机性较大,所以标准CS算法缺乏有效机制来加强搜索深度,算法收敛精度不高。CS算法在式(11)中定义了步长控制因子,该因子在标准算法中一般设定为固定的常数(譬如常取值为0.01)。若步长控制因子取值过大,易导致算法后期的搜索偏离优质解,使其收敛速度变慢;反之,若步长控制因子取值过小,则算法可能过早地陷入局部最优解,从而导致算法性能较弱。因此,对步长控制因子的改进有利于算法性能的提升。如果在算法搜索前期使用一个较大的步长控制因子,有利于在全局范围内迅速发现优质解所在区域;同时,随着算法搜索的推进,应逐渐减小步长控制因子,加强对局部优质解区域的细致搜索,这有利于提高算法的收敛速度和性能。 本文从步长控制因子方面对标准CS算法进行改进:用动态步长控制因子替换原有固定的步长控制因子。寻优过程中,随着个体质量逐步提高,适当缩小搜索范围,以加强搜索深度,有利于搜寻到更优的解。合理的步长控制因子应该是随着进化代数的增加而逐渐减小,使得算法在进化后期容易发现优质个体。 本文根据以下方面自适应调整步长控制因子α:将α取值范围设置为[0.01,0.2];另外,引入余弦函数使α随着进化代数的增加而减小。综上所述,提出α的改进公式: (14) 其中,R表示当前进化代数与总进化代数之比;αmin为步长控制因子的下限;αmax为步长控制因子的上限;Tmax为最大迭代次数;k为当前进化代数。算法初始阶段R≤0.2,此时应有大步长去发现优质解所在区域,因此步长控制因子α随进化代数增加而逐渐减小;算法中期可能达到最佳更新状态,即0.5>R>0.2,此时应在优质解所在区域进一步搜索,加强局部精细搜索,α保持不变;算法后期R≥0.5,此时个体逐渐接近Pareto前沿,无需大步长跳跃,因此保留α下界即可。 3.2.2多邻域局部搜索 为进一步提高布谷鸟算法的局部搜索能力,本文引入多邻域局部搜索策略,对种群中的优质个体执行基于不同邻域的细致搜索。具体来说,就是对算法当前的非劣解集中的个体执行基于三种邻域的局部搜索。这三种邻域搜索分别为:Interchange local search、Insert local search[16]、2-opt local search,具体定义如下。 Interchange local search:对每个个体的工件排序,随机选择其中两个不同的位置,交换位置上的工件。例如10工件排序为[4,2,7,1,3,5,9,8,10,6],随机产生了两个位置p1=3,p2=9,则将位置3的工件7和位置9的工件10交换位置,得到一个新排序[4,2,10,1,3,5,9,8,7,6]。 Insert local search:该步骤可分为前插入和后插入。对每个个体的工件排序进行操作,随机选择其中2个不同的位置p1和p2,假设p1>p2。后插入是指将位置p1的工件插入位置p2,位置p1+1~p2的工件均往前挪一个位置;前插入是指将p2的工件插入位置p1,位置p1~p2-1的工件均往后挪一个位置。例如10工件排序为[4,2,7,1,3,5,9,8,10,6],随机产生了两个位置p1=3,p2=9,按照上文,后插入得到的新排序为[4,2,1,3,5,9,8,10,7,6],前插入得到的新排序为[4,2,10,7,1,3,5,9,8,6]。 2-opt local search:对每个个体的工件排序,随机选择其中两个不同的位置p1和p2,将p1~p2的工件排序逆序排列,其他位置工件排序不变。例如10工件排序为[4,2,7,1,3,5,9,8,10,6],随机产生了两个位置p1=3,p2=9,按照上文,得到的新排序为[4,2,10,8,9,5,3,1,7,6]。 令π(X)为个体X基于LOV规则的工件排序,π(X′)为个体X′基于LOV规则的工件排序,k为扰动或探索次数。对个体X执行多邻域局部搜索的具体步骤如下: (1)扰动阶段。①设k=0;②随机选择2个不同位置p1和p2,π(X)=Insert(π(X),p1,p2),k=k+1;③如果k<2,则返回步骤②。 (2)探索阶段。①设k=0,t=0;②随机选择两个不同位置p1和p2;如果t=0,π(X′)=Insert(π(X),p1,p2);如果t=1,π(X′)=Interchange(π(X),p1,p2);如果t=2,π(X′)=2-opt(X,p1,p2);③如果π(X′)π(X),则π(X)=π(X′),k=k+1,否则t=t+1;④如果k<30,则跳到步骤⑤,否则停止探索并输出π(X)和X;⑤如果t<3,返回步骤②,否则t=0,返回步骤②。 基于改进的HCS算法求解MOPFSP的主要步骤如下: (1)参数初始化。设置种群规模N;个体上下界,并在界内初始化种群W;设置最大迭代次数gene或算法运行时间T。 (2)个体离散化。采用LOV规则将连续的个体转化为离散排序;计算每个个体的两个目标函数值。 (3)个体更新。随机挑选一个个体xi,根据式(11)采用莱维飞行对个体进行更新,产生一个新个体xi1;新老个体采用非支配原则保优,若互不支配,则随机保留一个,保留的个体存入xi1。 (4)抛弃概率的应用。根据抛弃概率判断是否对步骤(3)中保留的个体xi1进行操作,若要对其进行操作,则利用式(12)更新并得到一个新个体xi2,最后对新旧个体采用非支配原则保优;若互不支配,则随机保留一个,保留的个体存入xi1。 (5)保留Pareto前沿。利用非支配原则将本代的Pareto前沿找出,并将本代Pareto前沿的个体存入Pareto解集P(t)。 (6)多邻域搜索。将本代P(t)集合里的每个个体XP(t)对应的排序依次进行多邻域搜索,得到本代更新后的Pareto解集P(t)′。 (7)记录当前Pareto解集。将更新后的Pareto解集P(t)′与第t-1代保留下来的Pareto解集P融合,利用非支配原则求出当前第t代Pareto解集P,并用此集合P代替本代非劣解集P(t)′,便于在下一代中使用。 (8)根据式(14)更新步长控制因子α,每一代都要对步长控制因子做出判断,并更新。 (9)终止条件若当前迭代次数小于最大迭代次数gene或进化时间小于算法运行时间T,重复执行步骤(2)~步骤(8);否则输出当前Pareto解集P,结束算法。 基于以上步骤,利用HCS算法求解MOPFSP的算法流程图见图1。 图1 HCS算法流程图Fig.1 Flow chart of HCS 为验证HCS算法求解MOPFSP的有效性,本文选取了10种规模大小不同的算例,采用标准CS和INSGA-Ⅱ算法[17]进行对比实验。INSGA-Ⅱ算法是基于经典多目标算法NSGA-Ⅱ的改进算法,文献[17]利用仿真实验验证了INSGA-Ⅱ算法优于NSGA-Ⅱ算法,所以将HCS算法与INSGA-Ⅱ算法比较是有意义的。 在测试算例中,工件在每台机器上的加工时间采用100以内的随机正整数按照问题规模生成;机器速度挡位设定为Ai,k∈{1,2,3};所有算法的种群大小均为30;HCS算法与CS算法的抛弃概率均为0.25;CS算法步长控制因子为0.01;HCS算法初始步长控制因子为0.2;INSGA-Ⅱ算法中变异概率为0.3,交叉概率为0.9。本文以 50n(单位ms)作为各算法运行的终止条件,其中,n为每种问题规模的工件数。这使得测试同一个问题规模时,所有算法的运行时间一致,可确保比较的公平性。各算法对每一测试问题均独立运行20次。 所有算法和测试程序均用Delphi 10.2编程实现,操作系统为Win 10,处理器为Intel(R) Core(TM) i5-4210U 1.70 GHz,内存为4 GB。 本文采用的分析指标是文献[18]中提出的多目标分析指标,分别为R_NDS(Sr)和NDS_NUM(Sr),计算公式如下: R_NDS(Sr)=|Sr-{x∈Sr|∃y∈S:yx}|/|Sr| (15) NDS_NUM(Sr)=|Sr-{x∈Sr|∃y∈S:yx}| (16) 其中,Sr是指算法r的Pareto解集;S是指K种算法的Pareto解集的并集,可以表示为S=S1∪…∪Sr∪…SK;yx是指个体y完全支配个体x;|Sr|是指Sr集合中个体的数量;NDS_NUM(Sr)是指算法r中未被支配的个体数量;R_NDS(Sr)是指算法r中未被支配的个体数占算法r中总的Pareto解集个体数的比率。R_NDS(Sr)=1意味着Sr中所有的Pareto个体都不被支配;R_NDS(Sr)=0.9意味着Sr中90%的Pareto个体都不被支配。 本文中每个问题规模的数据结果可以在表1和表2中找到:HCS算法和CS算法的对比数据见表1, HCS算法和INSGA-Ⅱ算法的对比数据见表2。根据上文中S的定义,表1中的S可以表示为S=SHCS∪SCS,表2中的S可以表示为S=SHCS∪SINSGA-Ⅱ。R_NDS_HCS表示20个R_NDS(SHCS)数据的平均比率,R_NDS_CS表示20个R_NDS(SCS)数据的平均比率,R_NDS_INSGA-Ⅱ表示20个R_NDS(SINSGA-Ⅱ)数据的平均比率,NDS_NUM_HCS表示20个NDS_NUM(SHCS)数据的平均数,NDS_NUM_CS表示20个NDS_NUM(SCS)数据的平均数,NDS_NUM_INSGA-Ⅱ表示20个NDS_NUM(SINSGA-Ⅱ)数据的平均数。 表1 HCS算法和CS算法对比数据 表2 HCS算法和INSGA-Ⅱ算法对比数据 由表1可看出,R_NDS_HCS全部为1,而R_NDS_CS几乎为零,说明在求解以上所有问题规模的MOPFSP时,HCS算法完全支配标准CS算法,且NDS_NUM_HCS的个数在3~6之间,符合种群规模为30的情况;由表2可看出,R_NDS_HCS均大于R_NDS_INSGA-Ⅱ,且有8个问题规模的R_NDS_HCS大于0.8,说明HCS算法有80%以上的Pareto个体支配INSGA-Ⅱ算法的Pareto个体,而在其他2个问题规模中,比率为65%以上。总体而言,HCS算法得到的解集更优,证明了HCS算法的有效性。 10_5规模和100_30规模某次运行情况见图2、图3。从图2中可看出,虽然HCS算法与INSGA-Ⅱ算法寻得的Pareto解集重合,但都完全支配标准CS算法。从图3中可看出,HCS算法的Pareto前沿在其他2个算法的左下方,说明HCS算法的Pareto解集把其他2个算法的Pareto解集完全支配。随着问题规模的增大,较标准CS算法和INSGA-Ⅱ算法,HCS算法的Pareto前沿与其他2个算法的Pareto前沿距离越拉越大,寻优的优越性越来越明显。 图2 问题规模为10_5时3种算法的某次Pareto解点图Fig. 2 Non-dominated solutions of HCS (3points)、CS (2points) and INSGA-Ⅱ (3points) when the instance is 10_5 图3 问题规模为100_30时3种算法的某次Pareto解点图Fig. 3 Non-dominated solutions of HCS (4points)、CS (4points) and INSGA-Ⅱ (4points) when the instance is 100_30 综上所述,在以上所有问题规模中,HCS算法在求解MOPFSP时比INSGA-Ⅱ算法和CS算法有效。 为进一步验证所提算法的有效性,将HCS算法用于求解江西瑞金某电线电缆厂的电线电缆生产调度问题。该工厂初成型电缆生产过程依次为单丝拉制、单丝退火、导体绞制、绝缘挤出、成缆共5个环节。5个环节分别在5台特定的机器上加工,各环节的加工机器可通过调整挡位来设定加工速度。近年来,该公司积极响应绿色生产节能减排,在其生产过程中同时考虑经济指标(make-span)和环境指标(TCE)。显然,此初成型电缆的生产调度问题是典型的MOPFSP。目前,该电缆厂生产调度是由调度员基于经验对工件编号后进行人工排序调度。 本文采用该工厂生产30类电缆的实际生产数据作为测试实例,用HCS算法运行1.5 s求解,同时请调度员在5 min内给出人工调度方案。HCS算法获得了调度方案S1~S4,见表3和图4。调度员通过经验得到的调度方案T1,见表3。由表3可知,S1~S4均明显优于T1。这一结果表明HCS算法可快速有效地求解实际问题。 表3 调度方案 图4 HCS目标值对比Fig.4 HCS target value comparison 本文提出了一种混合布谷鸟算法,用于求解绿色多目标流水车间调度问题(MOPFSP)。HCS算法通过采用所提的自适应步长控制因子和多邻域局部搜索,较好地平衡了算法的全局和局部搜索,提高了算法的性能和收敛速度。仿真实验和算法比较结果表明,HCS算法能够较快求解MOPFSP,且其性能优于CS算法和INSGA-Ⅱ算法。验证了HCS算法在求解MOPFSP上的有效性。 关于布谷鸟算法在复杂生产调度上的未来研究,可以考虑将其拓展应用于比MOPFSP更加复杂的调度问题上,特别是不确定绿色调度问题。3 混合布谷鸟算法
3.1 标准布谷鸟算法
3.2 混合布谷鸟算法(HCS)
3.3 HCS算法求解MOPFSP的步骤
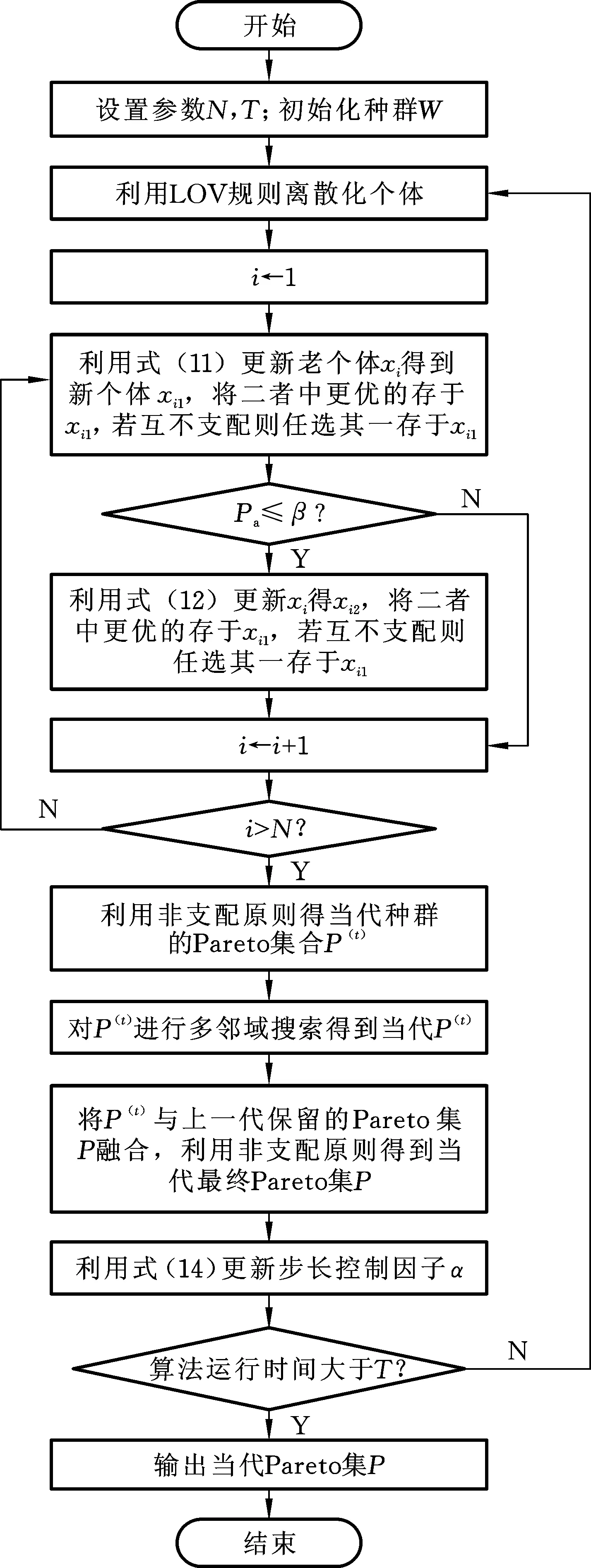
4 算法测试结果及分析

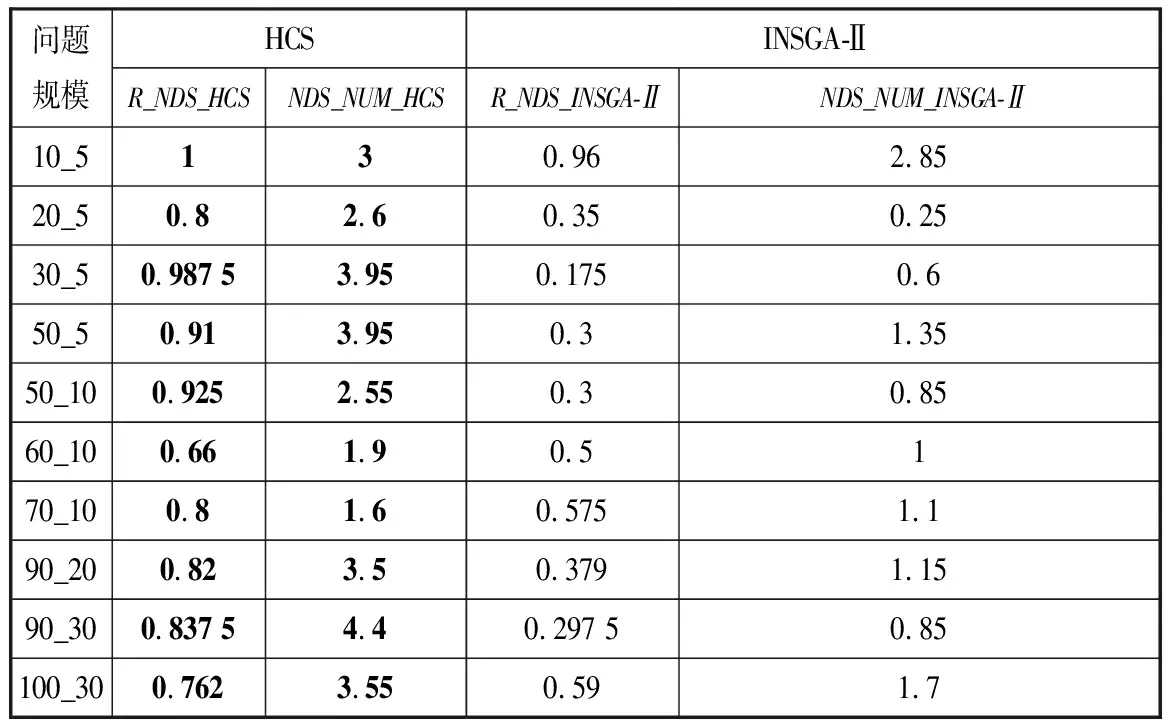


5 实例分析
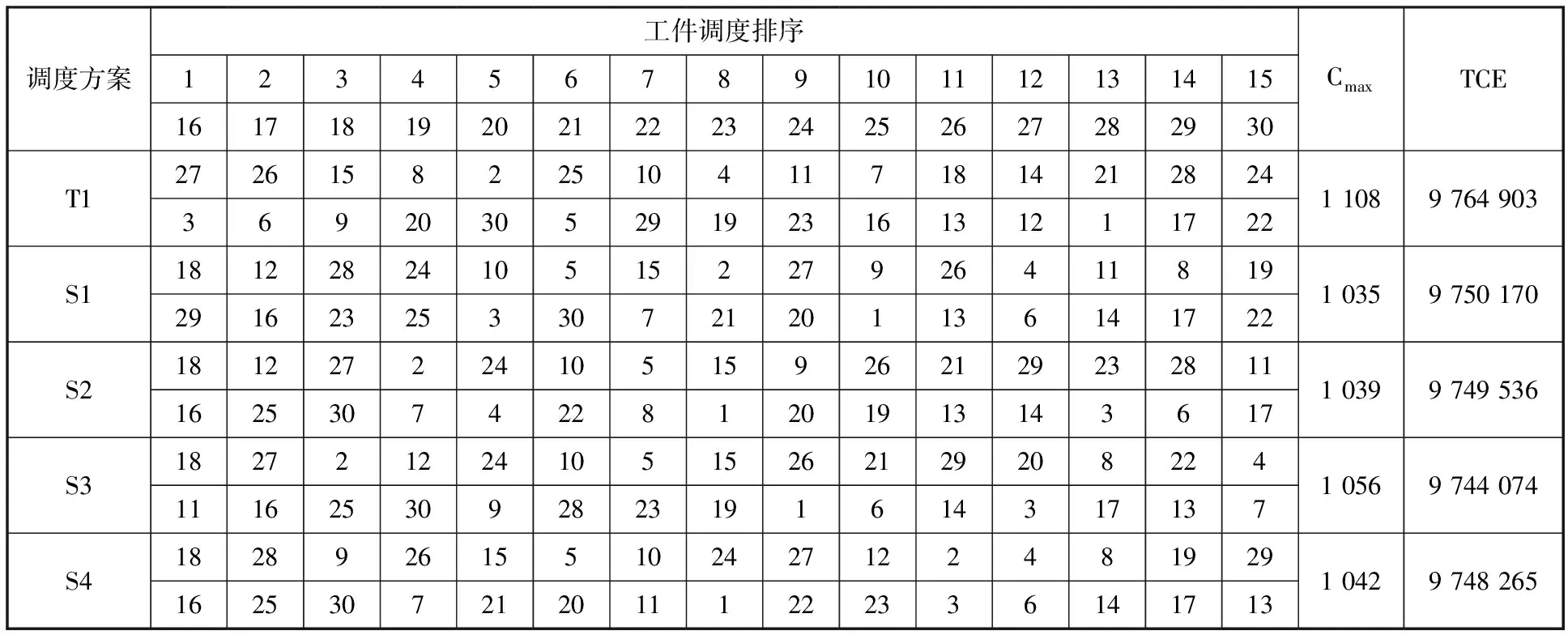
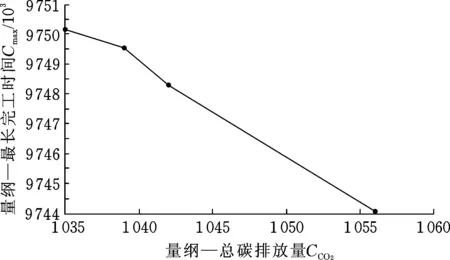
6 结论
