西安地区Q3原状黄土蠕变特性试验研究

(西安科技大学 建筑与土木工程学院，陕西 西安 710054)

1 研究背景

黄土覆盖面积广阔，全球黄土分布的总面积约有1 300万km2，覆盖率达全球大陆面积的 9.3%以上。而我国黄土的总面积约为64万km2，约占国土面积的 6.3%，其中西部地区黄土分布最为广泛，约占土地面积的 50%～60%。近年来，随着我国西部大开发，“一带一路”倡仪的实施，黄土地区岩土工程问题亟待探讨和研究。西安土质为黄土(沙质)，属于湿陷性黄土。湿陷性黄土的主要特征有：主要色调为黄色、含盐量较大、粉土颗粒含量较多、具有大孔性，在天然剖面上有垂直节理；土质稳定性好，在没有遇到水的情况下，土质坚硬；受水浸湿容易湿陷，使建筑物大幅度沉降、倾斜而影响其安全和正常使用。湿陷性黄土是指黄土在一定压力作用下， 受水浸湿后，土壤结构迅速破坏，发生显著的湿陷变形，强度也随之降低。黄土地区岩土工程问题的研究与一系列基础设施、生态环境以及高新技术等方面密切相关。

Pumpellv[1]可能是外国地质学家中提到中国黄土的第一人，他观察了中国北方的黄土，研究黄土的成因，打开了黄土近代科学研究的大门。他认为黄土是湖泊沉积物，并使用了“Huangtu”作为其英文名称。自20世纪50年代以来，刘东生等[2-5]在对中国黄土进行全面调查的同时，做了较多的地球化学分析工作。文启忠等[5-7]对80年代以前中国黄土的化学成分研究做了总结[8]。土的流变性研究在国内外也早已开始，Scott编著的《土力学原理》中，长期试验数据表明了黏土有明显的弹性后效特性[9]。而蠕变本构是土体的流变力学理论的基础，同时也是其最重要的组成部分，在各种研究中尽可能地选择能够反映蠕变规律的简单模型，如描述岩土材料粘弹性的Kelvin体、Maxwell体及其Burges模型，描述岩土材料粘塑性的Bingham体，描述岩土材料粘塑性的村山模型和西原模型等。另外，有些学者将模型串联或并联，用以准确描述岩土材料的流变性质。夏才初等[10-12]提出的统一流变力学模型，可以在统一流变力学模型及其14个特殊情况下对模型进行全面系统地辨识。土体蠕变一般经历3个阶段，即减速蠕变阶段，等速蠕变阶段和加速蠕变阶段。很多模型只能较好地描述土体蠕变的前两个阶段，而不能描述第三阶段，而第三阶段正是土体的破坏阶段，所以蠕变模型中包含第三阶段，对于工程长期稳定性有一定的指导意义。

本文通过黄土蠕变试验，基于传统西原模型，提出加速西原模型，能够较好地描述土体蠕变的3个阶段，弥补了原有模型只能描述蠕变前两个阶段的不足，并根据试验数据得到长期强度函数参数，确定所取黄土的长期强度函数方程。

2 试验方案

试验所选用的Q3原状黄土取自西安市南部地区航天城，取土深度5 m。按照土工试验规范，根据“烘干法”，测得土样天然含水率为18.28%；根据“环刀法”，测得土样天然密度为1.60 g/cm3，通过计算得到土体天然孔隙比为 0.996。根据液塑限联合测定法得土体液塑限分别为ωL=41.8%,ωP=25.7%；根据比重瓶法，土体相对密度为2.70。其基本物理力学指标如表1所示。

表1 基本物理力学指标

试验在SR-6型上进行，试样为 30 cm2×12.5 cm的圆柱体。所有试样采用相同含水率(18.28%)，在用环刀取得试样后，再将环刀取下，分别用12.5，25，50，75，100，125，150，175，187.5，200 kPa进行单轴蠕变试验。对于每一组荷载设定加载稳定标准为24 h内蠕变量小于 0.002 mm，卸载蠕变量24 h内小于 0.005 mm，即可认为稳定。当蠕变曲线出现等速蠕变阶段后，势必会出现加速蠕变阶段，此时试样的应变速率急剧增大，试样在短时间内遭到破坏。

3 试验结果及分析

3.1 蠕变曲线

以时间为横坐标轴，应变ε为纵坐标轴，绘制Q3原状黄土在无侧限下的蠕变加卸载曲线，如图1所示。

图1 不同应力下试样加卸载曲线

由图1可以看出，应力越大，试样达到稳定的时间越短，反之越长。蠕变曲线在出现第二阶段，即等速蠕变阶段时，必然会出现第三阶段，即加速破坏阶段，试样破坏。

3.2 应变速率与时间关系曲线

在分析黄土蠕变特性时，从得到的蠕变曲线中选取几条具有代表性的曲线绘制相应的时间与应变速率关系曲线，如图2所示。

图2 不同压力下应变速率与时间关系曲线

由图2可知，在低水平应力作用下，应变速率随时间的增大而减小，最终趋于0，满足第一阶段减速蠕变阶段特性；在高水平应力作用下，应变速率随时间的增大先减小、后平衡，再快速增大，符合黄土蠕变所经历的减速蠕变、等速蠕变、加速蠕变3个阶段。

3.3 蠕变模型分析

基于流变模型理论，结合蠕变试验曲线对要选模型进行辨识。

(1)刚加载时，出现瞬时变形，证明存在瞬时弹性变形，即模型中有独立弹簧元件；

(2)在低应力条件下，蠕变曲线呈减速蠕变状态，且卸载后能完全回弹，说明模型中包含黏弹性体；

(3)在较高应力条件下，蠕变曲线出现等速蠕变阶段，且最终出现加速破坏蠕变阶段，证明模型包含黏塑性体。

综上所述，本构模型选择为西原模型。

4 蠕变本构模型的建立

4.1 西原模型

如果将具有弹性的虎克体简记为H(表示为弹簧线)，将具有黏性特点的牛顿体简记为N(表示为黏壶线)，将具有塑形特点的圣·维南体简记为V(表示为断搭线)，通过将其串联和并联，组合成不同的力学模型，以便描述材料更加复杂的力学特性。当采用斜线与平线分别表示有关元件的串联和并联关系时，常用的模型有Maxwell模型(简记为 M，其组成为H-N)、Kelvin模型(简记为 K，其组成为 H/N)、广义Kelvin模型(其组成为H/N-H)等多种力学模型。西原模型(见图3)由虎克体、开尔文体和理想黏塑性体串联而成，能较全面地反映岩石的弹-黏弹-黏塑性特性。

图3 西原模型

对于西原模型，其基本关系式为

式中，E1,E2为弹性模量，Pa；η1，η2，η3为黏滞系数，PaS；S3为屈服应力，kPa。

如果应力为瞬时施加的恒定应力σ0(dσ/dt=0)，则有：

(2)

可见，当σ0≤S3时，第一项为弹性应变部分，第二项为非稳定蠕变部分。当σ0>S3时，塑性元件开始滑动，第一项为弹性应变部分，第二项为非稳定蠕变部分，第三项为稳定蠕变(等速蠕变)部分。

但西原模型使用的元件为理想线性元件，难以描述蠕变的加速破坏阶段。

4.2 加速西原模型

谢定义等[13](2008年)指出：土是一种多孔多相的松散介质，是一种有许多颗粒以一定方式排列连接而成的集合体，当受到外界荷载作用时，土中的某些部分会出现应力集中，个别连接点超载和遭到破坏，进而使土中内部颗粒的相对位置发生改变，连接遭到破坏的点颗粒趋向新的稳定。在这个过程中，一方面出现新的“愈合”，另一方面也出现新的“损伤”。这种缓慢进行的“愈合”和“损伤”过程就是土的蠕变过程。

考虑到黄土进入非线性破坏阶段后，应力应变关系已不再是简单的正比例关系，因此可以选择黄土的应变参量作为黄土是否进入加速蠕变阶段的标准，并引入带应变触发的非线性黏壶来描述加速蠕变阶段的变形(见图4)。

图4 非线性黏壶元件

应变触发，就是模型的应变达不到εa(黄土刚进入加速蠕变阶段时所对应的应变值)时，黏壶为刚体，不起作用；当ε>εa时，黏壶触发。蠕变过程中应力与应变速率成正比例关系，即

(3)

所以在施加应力时，

(4)

加速西原模型如图5所示，与传统西原模型的主要区别在于用非线性黏壶代替黏壶。

图5 加速西原模型

图6 200 kPa下加速蠕变阶段应变速率与时间关系曲线

关系式为

(5)

所以ε(t)=CeBt+D

将第三阶段应变公式与前两阶段结合，可得

ε=A+B[1-exp(-Ct)]+Dt+EexpFt

(6)

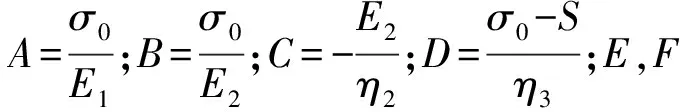
5 西原模型和加速西原模型数值分析

5.1 西原模型的数值分析

将试验所得数据与传统西原模型进行拟合，在低荷载下，拟合结果如图7所示；较高荷载下，结果如图8所示。

图7 低荷载下西原模型拟合曲线

图8 较高荷载下西原模型拟合曲线

所得相关系数分别为：0.974 77，0.984 81，0.985 78，0.980 21。拟合结果可以看出西原模型可以很好地描述蠕变的前两个阶段，但对第三阶段无法进行描述，所以引入加速西原模型。

5.2 加速西原模型的数值分析

当ε>εa时，蠕变进入加速蠕变阶段，同时σ0>S3，此时蠕变方程为

ε=A+B[1-exp(-Ct)]+Dt+EexpFt

(7)

将试验结果与加速西原模型进行拟合，如图9所示。

图9 加速西原模型拟合曲线

相关系数为 0.995 04，说明拟合效果很好，所选取的模型较好描述了该黄土蠕变的3个过程。

6 长期强度

长期强度是指土体在长期荷载作用下抵御破坏的强度值，土体在长期荷载作用下会产生蠕变效应，故而把蠕变强度作为土体的长期强度。

本文所用确定长期强度的方法为：根据试验所得4条破坏曲线，以试样破坏时所需的时间为横坐标，施加的应力为纵坐标，绘制一条曲线，此曲线反映了破坏剪应力与破坏时间的关系，即为长期强度曲线。长期强度曲线上的流动纵坐标即为土的长期强度。

破坏时间与所施加应力之间关系如图10所示。

图10 试样的长期强度曲线

取剪应力对数τ和破坏时间对数t，由图11可知X=τ与Y=t呈良好的线性关系，拟合方程为

Y=-0.112 34X+4.523 21

(8)

图11 长期强度曲线取对数

相关系数为 0.964 27，拟合度较高。

土长期强度的幂函数方程为

(9)

式中，T*=T(N/a)l/a;N=A0(εpc)m；tp为蠕变变形时间；a,m为无因次参数；εp为破坏时刻的蠕变变形值。

所以，长期强度幂函数的方程参数为：a=-0.112 34,T=exp(4.523 21/0.112 34)=3.06×1017，其长期强度幂函数方程为

(10)

该方程可计算任一破坏时刻的长期强度值。

7 结 语

西原模型可以较好模拟土体蠕变的减速蠕变、等速蠕变阶段，但却不能描述土体的加速蠕变阶段。在西原模型原有元件的基础上，串联一个非线性黏壶，构建出加速西原模型，加速西原模型在能描述土体前两个变形阶段的基础上，能够较好描述土体蠕变的加速蠕变阶段。并且通过长期强度的定义，根据长期强度幂函数公式得到土体长期强度幂函数方程，对工程有一定指导意义。

但在室内土工试验中，由于仪器设备及人工操作问题，所得参数值的不精确问题不可避免。另外，本文根据传统西原模型，基于西安地区土样得到的加速西原模型是一种经验模型，有一定的地域局限性，难以适用于所有地区黄土。