无人机三维编队保持的自适应抗扰控制器设计

魏 扬,徐浩军,薛 源

(空军工程大学航空工程学院,陕西 西安 710038)

0 引 言

无人机在编队飞行时,需要保持编队队形的稳定,以获得最佳的气动效益和作战效能。在长机做机动飞行(如爬升、转弯等常规机动动作)时,为了使僚机能够精确跟踪长机轨迹,并与长机保持期望的编队距离和飞行速度,使整个编队能够在外界干扰(紊流、风切变等)下始终稳定维持在一个固定的构型,需要设计队形保持控制器,以保持编队队形的稳定。

无人机的编队保持控制问题是目前的研究热点,国内外均开展了这方面的研究工作。目前研究较多的无人机编队策略主要有领航跟随法[1]、虚拟结构法[2-3]、行为分解法[4]。其中领航跟随法即“长-僚机”编队研究最多也最成熟。比例-积分-微分控制[5-6]、非线性动态逆控制[7-9]、鲁棒控制[10]、极值搜索[11]、非线性模型预测控制[12]等多种方法被应用到无人机编队保持控制中。但大多数文献仅局限于二维平面上的编队保持[13-19],然而在实际情况中,编队飞行发生在三维空间,只是考虑平面上的相对运动并不符合飞机的飞行实际,也不能满足更精确的需求。

针对无人机在三维空间上的编队保持研究的相对较少,且很少考虑设计控制器的抗扰动性能。文献[20]设计了比例积分的紧集编队队形保持控制器,但面对外界扰动时控制器的鲁棒性不强;文献[21]设计了近距编队的鲁棒自适应控制器;文献[22]采用滑模变结构控制方法设计了编队保持与变换控制器;文献[23]基于鲁棒H∞控制理论设计了编队保持控制器,采用相同方法的还有文献[24];文献[25]提出了编队飞行内外环控制的思想;文献[26]采用多种自适应控制方法设计了编队飞行的容错控制系统;文献[27]采用传统的线性化手段设计了三维编队控制律,但没有考虑外界扰动的影响,采用相同方法的还有文献[28];文献[29]采用比例-积分-微分控制方法设计了无人机编队控制系统,并开展了飞行试验。以上的这些文献虽然考虑了三维情形下的编队保持,但都是把编队运动的三维模型简单解耦分别进行控制,对外界扰动考虑的较少,降低了控制精度以及控制器的抗干扰能力。

针对无人机编队保持控制在“三维”与“抗扰”方面的设计需求,本文在考虑系统存在外界时变干扰的情况下设计了三维空间上的无人机编队保持自适应控制器,能够有效抑制干扰的影响,使僚机能够迅速跟随长机机动,并克服外界干扰以保持编队队形的稳定,具有较强的鲁棒性,在工程上有一定的应用价值。

1 无人机编队建模

1.1 简化的自动驾驶仪模型

现代关于飞机内回路姿态控制(即飞机自动驾驶仪设计)的研究已经比较成熟[16]。这里将自动驾驶仪模型进行简化,并作为本文飞行控制的内回路。

假设编队中的每一架无人机均配备有闭环的互不耦合的速度保持控制、航迹俯仰角保持控制、航向角保持控制的自动驾驶仪系统,能够实现自动控制无人机按照设定的速度、航迹俯仰角、航向角飞行。这里将自动驾驶仪简化为一阶的速度保持控制、航向保持控制及航迹俯仰角保持控制模型[30],表示为

(1)

式中,τV、τχ及τγ分别为速度通道时间常数、航向通道时间常数及航迹俯仰角通道时间常数；i=L,W分别表示长机与僚机。

1.2 旋转坐标系下编队的相对运动方程

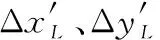
无人机的运动学方程为

(2)

由图1中的双机相对运动关系可得

(3)

其中

(4)

其中

2 队形保持控制系统设计

2.1 无人机编队保持控制系统结构

无人机编队飞行的队形保持控制系统的设计结构如图2所示。该控制系统为一个闭环系统,由内、外回路两部分组成。以双机编队飞行为例,内回路为僚机上的自动驾驶仪,其功能为:接收外回路传递来的速度指令VWc,航向角指令χWc以及航迹俯仰角指令γWc,并由僚机的自动驾驶仪跟踪输入指令,从而实现僚机的自动飞行。其余部分为外回路,其功能为:通过长机的自动驾驶仪控制长机跟踪指定的编队机动指令,得到长机速度VL、偏航角χL以及航迹俯仰角γL这些运动状态参数;再将长机的运动状态参数及编队间隔指令(xc,yc,zc)输入到队形保持自适应控制器中,经过控制律解算为内回路即僚机的自动驾驶仪生成速度指令VWc、航向角指令χWc以及航迹俯仰角指令γWc。另外,在考虑扰动干扰的情况下,需要对僚机的自动驾驶仪模型进行修正,加入扰动影响的模型,如长机的尾涡流的气动干扰模型。这样,内外回路相互协调工作就能够实现自主编队飞行的队形保持。

图2 编队飞行队形保持控制系统结构Fig.2 Structure of Formation keeping control system

多机编队的队形保持控制系统可在此基础上拓展,只要将僚机当作编队序列里的第i架无人机,长机为与之相邻的第i-1(i>1)架无人机,两者之间进行信息交互,控制方法不用改变。以此类推即可实现多机编队的队形保持控制。

2.2 队形保持的自适应控制器设计

在编队飞行时,不可避免地要受到外界不确定干扰(如突风、湍流)的影响,从而对编队成员的飞行状态造成影响。自适应控制是一种能修正自己特性以适应对象和扰动动态特性变化的一种控制方法[31]。在考虑闭环系统存在外界时变干扰的情况下,采用自适应控制思想设计队形保持控制器,以提高系统鲁棒性。

考虑到模型不确定性,选取函数ΔfVi、Δfχi、Δfγi为时变干扰函数,加入到简化的自动驾驶仪模型中去,用来作为编队飞行系统模型中的不确定项,可以得到

(5)

并做以下假设:

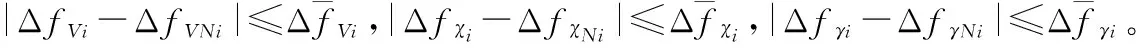
假设2由于这里只是对僚机进行控制,所以ΔfVL=ΔfχL=ΔfγL=0。

对无人机编队的运动学方程式(2)求二阶导可以得

(6)

式中,λV=1/τV；λχ=1/τχ；λγ=1/τγ。下面定义在惯性坐标系下僚机与长机的编队误差为e,ΔAc=[Δxc,Δyc,Δzc]T表示期望的编队间距,则有

e=AL-AW-T1(χL)T2(γL)ΔAc

(7)

则误差的一阶导数为

(8)

则误差的二阶导数为

(9)

这里选取u1=[VWc,γWc,χWc]T为控制量,整理矩阵等式(9)可得

(10)

其中

G=

F=

为使误差能够稳定收敛,设计控制律为

(11)

(12)

则可以得到误差的动力学方程为

(13)

将误差方程写为

(14)

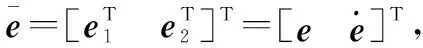
(15)

其中

只要保证误差渐进趋近于0,即可达到控制目的。令对称正定矩阵P为Lyapunov矩阵方程ATP+PA=-Q的解,Q也为对称正定矩阵,设计自适应律为

(16)

(17)

(18)

至此,在编队飞行系统模型中的不确定项为时变函数的情况下的自适应队形保持控制器设计完毕。

3 仿真验证

为验证设计的自适应控制的队形保持控制律的有效性,设置仿真条件为:长机的飞行速度指令为在0～10 s保持为120 m/s,在10～20 s以1 m/s2的斜率增大到140 m/s,此后保持140 m/s的速度不变。长机的航向角指令为在0～15 s保持为0°,在15～30 s以2(°)/s的斜率增大,此后保持30°的航向角不变。长机的航迹俯仰角在t=0～10 s保持在0°,在t=10～20 s以1(°)/s的斜率增大,在20～30 s保持10°不变,在t=30～40 s又以-1(°)/s的斜率恢复到0°,此后保持0°不变。为使指令能够平滑输入,增加一阶滤波器对指令进行滤波。长、僚机的初始速度均为120 m/s,初始的航向角、航迹俯仰角均为0°。长僚机的初始的x、y、z三方向上编队距离差分别为(30 m,30 m,-30 m)。控制目的是在以长机为参考的旋转坐标系下,x、y、z三方向上长僚机的编队距离差保持为(50 m,100 m,0 m)。

为了充分考虑干扰对无人机编队飞行产生的影响,这里取3个通道的时变干扰函数为

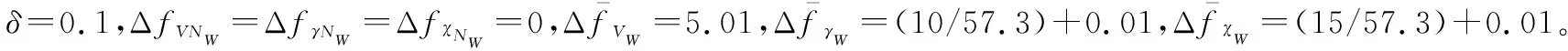
这里取长机与僚机的自动驾驶仪3个通道的时间常数分别为:τV=5 s,τχ=0.33 s,τγ=0.33 s。为了使指令能够平滑输入,增加一阶滤波器对指令进行滤波。仿真时间为50 s,仿真步长取0.01 s。图3～图9为仿真的结果。

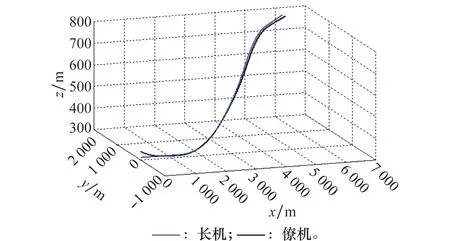
图3 双机的三维空间飞行轨迹Fig.3 Three-dimensional flight trajectory of two UAVs

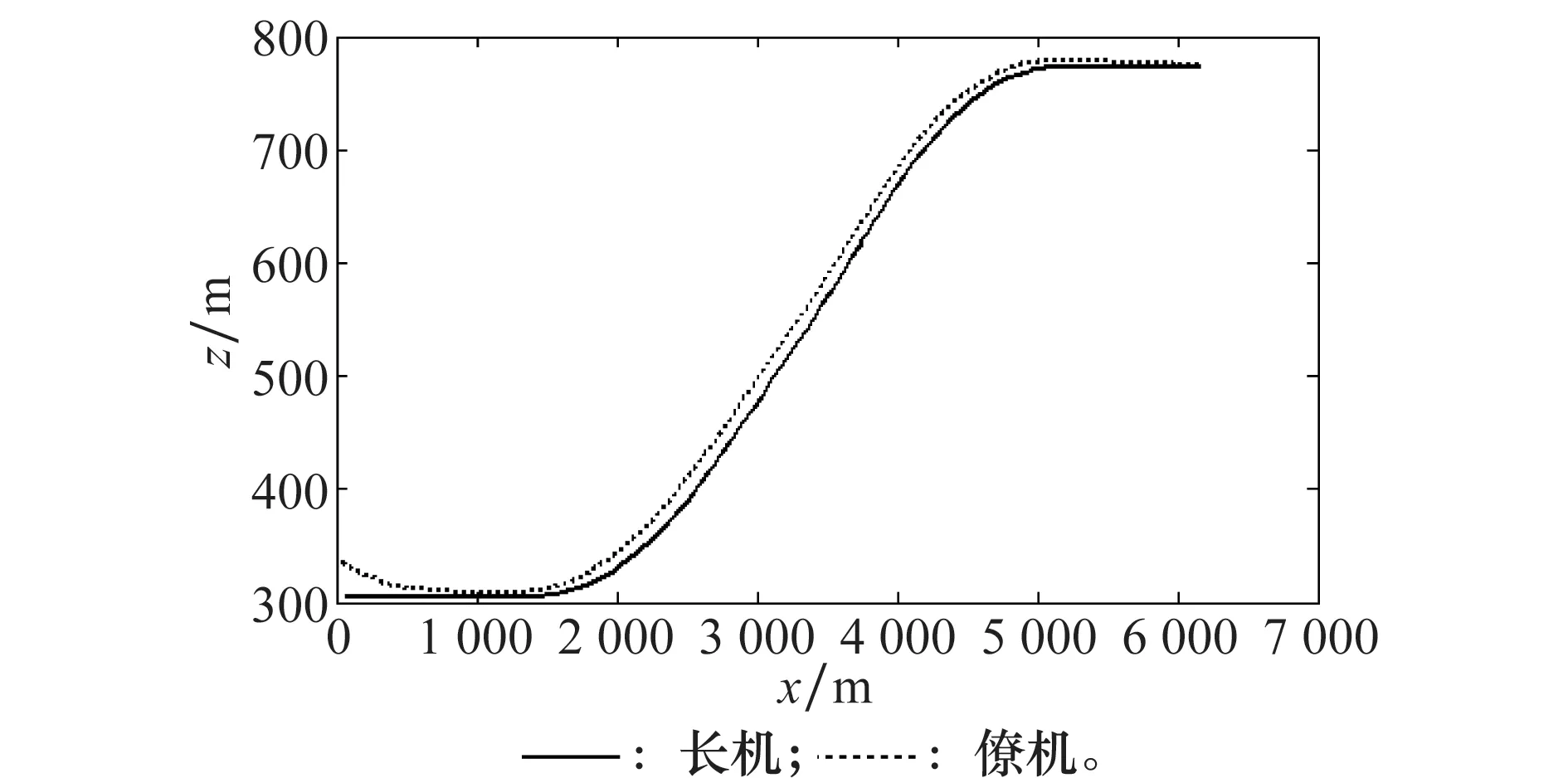
图5 x-z平面上双机的飞行轨迹投影Fig.5 Projection of two UAVs’ flight trajectory in x-z plane

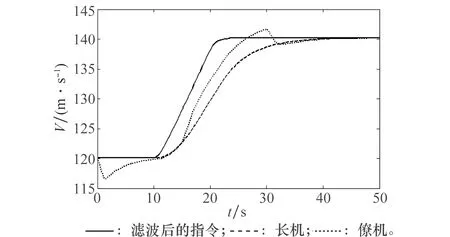
图6 长僚机速度变化曲线Fig.6 Velocity changing curve of leader and wingman

图7 长僚机航向角变化曲线Fig.7 Heading angle changing curve of leader and wingman

图8 长僚机航迹俯仰角变化曲线Fig.8 Flight pitch angle changing curve of leader and wingman

图3为长、僚机在三维空间的编队飞行轨迹。图4、图5分别是长、僚机在x-y平面、x-z平面上的飞行轨迹投影。可以看到在时变扰动的影响下,僚机仍然能够在控制律的作用下与长机保持期望的编队队形。从图6～图8可以看出,僚机的航向角和航迹俯仰角在扰动作用下虽然在前10 s内波动较大,但在10 s以后均能精确地跟踪长机。僚机的速度在扰动影响下虽然相对波动较大,但与长机的速度差不大,且最终能够稳定达到指定的速度140 m/s。图9表示长僚机在飞行过程中编队间隔的变化。可以看到,虽然在扰动影响下,僚机自适应调整编队的间隔所需的时间较长,但均能够稳定达到指定的编队间隔,以保持稳定的编队队形。

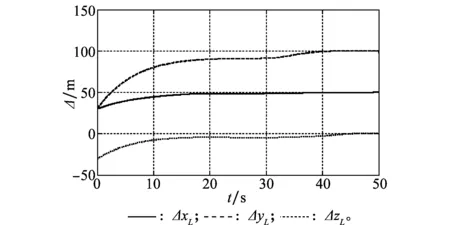
图9 旋转坐标系下长僚机编队间隔的变化Fig.9 Change of formation distance between wingman and leader in rotating coordinate system

为了充分说明本方法的优势,在相同的仿真条件下采用文献[30]中的方法设计全局稳定的编队保持控制器,图10～图14为仿真结果。

图10 根据文献[30]中的方法得到的长僚机速度变化曲线Fig.10 Velocity changing curve of leader and wingman according to the method in Ref.30

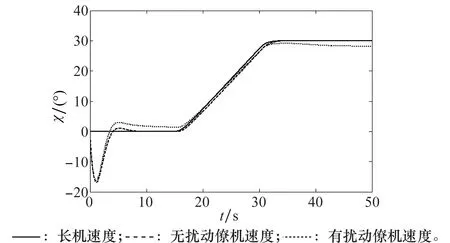
图11 根据文献[30]中的方法得到的长僚机航向角变化曲线Fig.11 Heading angle changing curve of leader and wingman according to the method in Ref.30

图12 根据文献[30]中的方法得到的长僚机航迹俯仰角变化曲线Fig.12 Flight pitch angle changing curve of leader and wingman according to the method in Ref.30

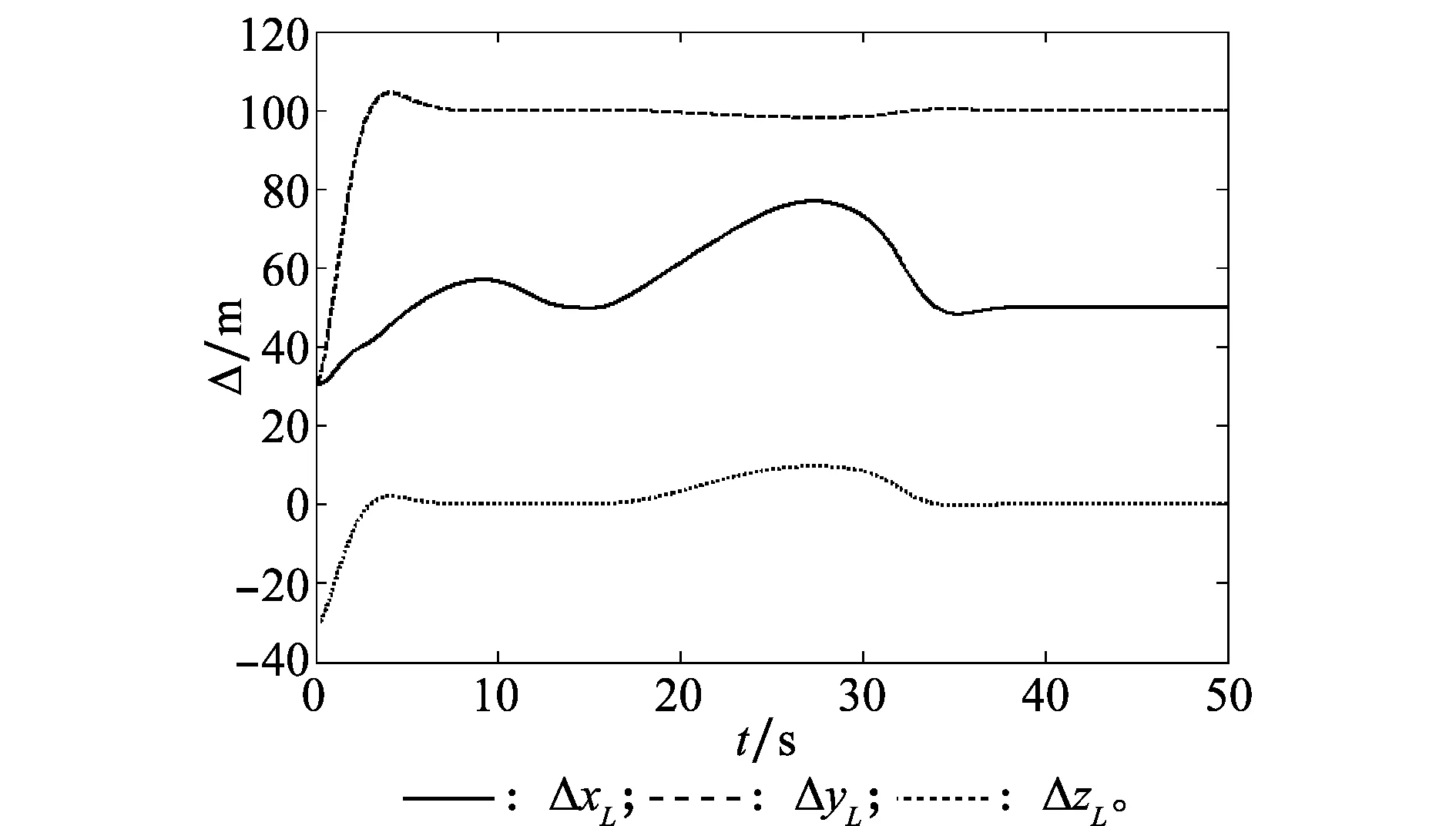
图13 无扰动下的长僚机编队间隔的变化Fig.13 Change of formation distance between wingman and leader with no disturbance

图14 有扰动下的长僚机编队间隔的变化Fig.14 Change of formation distance between wingman and leader with disturbance

从图10～图14可以看出,在不加外界扰动的情况下,采用文献[30]中的全局稳定的编队保持控制方法取得了较好的效果,能够实现僚机速度、航向角、航迹俯仰角的精确跟踪,并与长机保持期望的编队间隔。但在加入相同的外界时变干扰的情况下,控制效果变差,僚机的速度响应超调量较大,航向角和航迹俯仰角响应最终不能稳定收敛到指令值,存在较大的稳态误差。同时与长机不能保持期望的编队间隔。

以上的仿真结果表明,对于给定的速度、航向角和航迹俯仰角指令,编队队列中的僚机在本文设计的自适应控制器的作用下可实现精确的跟踪,同时能够克服外界扰动的影响,使僚机与长机能够保持期望的编队间隔不变,维持稳定的编队队形飞行。由此通过对比验证了本文提出的设计方法的有效性。

4 结 论

本文对三维空间下无人机编队队形的保持控制问题展开研究,设计了自主编队飞行队形保持控制系统结构,以简化的自动驾驶仪模型为编队保持控制系统的内回路,基于以长机为参考的旋转坐标系建立了相对运动学模型,采用自适应的控制方法来实现存在外界时变干扰情况下僚机对长机机动的跟踪和对编队队形的保持。通过与其他文献中的方法在相同条件下仿真结果的对比,突出验证了本文提出方法的优势,即抗扰动性能好,鲁棒性较强,调参难度小,具有一定的工程应用价值。