基于机会理论的复杂装备系统风险传递GERT研究
2018-12-10孟祥飞
王 瑛,孙 贇,孟祥飞,亓 尧,李 超
(空军工程大学装备管理与无人机工程学院,陕西 西安 710051)
0 引 言
随着国防技术的迅猛发展,武器装备融合多种高新技术,系统关联复杂,部队战斗力得到很大提升,如何对这些复杂装备进行科学的管理是急需解决的问题[1-2]。复杂装备系统内部各个子系统之间相互作用和相互影响使得系统在执行任务的过程中存在一定的脆弱性和风险,刻画系统各个风险因素间的关系,研究复杂装备系统中的风险传递,对于发现复杂装备系统的风险机理有着很重要的意义[3-4]。
图形评审技术(gragh evaluation review technique,GERT)是能够反映系统在内部与外部随机因素、随机变量作用下,各构成要素间相互关系的网络分析技术[5],该方法为解决包含随机因素的问题提供了有效的工具[6-7]。传统的GERT网络理论基于经典的概率论,主要描述随机型问题[8-9]。但是在实际的社会实践中,常常遇到各种非决定性的现象,这些非决定现象有足量样本数据的情况下可以利用概率统计得到概率分布函数,应用概率论解决问题,比如装备保障系统库存优化中备件配送的具体时间[10],装备维修决策中部件的磨损程度等[11];没有足量样本数据的情况下,只能邀请相关的专家给出事件发生的信度得到不确定分布函数,比如无人机任务分配中无人机执行具体任务的威胁程度[12],部队安全管理状况对任务完成的影响程度等。对于这种包含多种非决定现象的问题,传统的GERT网络不再适用。为解决专家信度给出的不确定变量,刘宝碇教授提出不确定理论[13],随着大量学者的深入研究,该理论已经成为一个严密的数学系统,并且已经应用到多目标规划、数据挖掘、网络分析等领域[14]。为处理同时存在随机变量和不确定变量的问题[15],刘宝碇教授提出不确定随机变量,进而发展出机会理论[16-17],目前该理论主要在目标规划[18-19]、网络分析[20-21]等领域进行应用,在装备风险分析方面的研究比较少见。
在复杂装备系统中一个合理的假设是,有些风险变量为随机变量可以得到概率密度函数,有些变量为不确定变量可以得到不确定分布。本文针对复杂装备系统在进行任务活动中表现出的兼具随机性和不确定性的特点,提出不确定随机GERT(uncertain random GERT,UR-GERT)网络模型。首先基于风险度的不确定随机特性,提出不确定随机矩母函数,并对该矩母函数的相关性质进行了探讨;然后针对风险度的不同类型提出相应的求解方法;最后通过复杂装备系统执行眼镜蛇机动的任务进行了风险分析,证明该方法的科学性和有效性。
1 相关理论介绍
定义1[16]机会测度。如果(Ω,A,Pr)表示概率空间,(Γ,L,M)表示不确定空间,那么两者的乘积(Γ,L,M)×(Ω,A,Pr)表示机会空间,如果Θ表示的是L×A的一个事件,则称事件Θ的机会测度为

(1)
式中,Ω表示非空集合;A表示Ω上的σ-代数;A中的每个元素称为事件;Pr表示概率测度;Γ表示非空集合;L表示Γ上的σ-代数;L中的每个元素称为事件;M表示不确定测度。
定义2[16]不确定随机变量。从机会空间(Ω,A,Pr)×(Γ,L,M)到实数集R的一个可测函数称为不确定随机变量。
注释1∀B∈R,A×L中的事件可以表示为{ξ∈B}={(γ,ω)∈Γ×Ω|ξ(γ,ω)∈B}。其中,γ表示不确定变量,ω表示随机变量。如果γ确定,那么ξ就变为随机变量,如果ω确定,那么ξ变为不确定变量。
定义3[16]机会分布。如果Φ(x)对不确定随机变量ξ满足
Φ(x)=Ch{ξ≤x},∀x∈R
(2)
那么,Φ(x)称为ξ的机会分布。

定义4[20]不确定随机变量的期望值。如果不确定随机变量ξ存在期望值,那么,称

(3)
为不确定随机变量的期望值。
注释2如果不确定随机变量的机会分布为Φ(x),那么,变量的期望值为

(4)
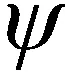
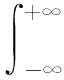
(5)
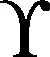

(6)
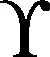
ξ=f(ω1,ω2,…,ωm,γ1,γ2,…,γn)
(7)
满足f(ω1,ω2,…,ωm,γ1,γ2,…,γn)对于γ1,γ2,…,γn是单调函数时,该变量存在期望值为
E[ξ]=
(8)
2 风险传递UR-GERT模型构建
风险传递UR-GERT模型由节点、流和边构成,在该模型中异或型节点表示风险基元vi,风险基元分为不确定型风险基元和随机型风险基元;网络的边表示风险基元之间的相互影响关系;网络的流表示为sij=(pij,hi),pij表示风险传递强度,hi表示风险度,可以建立如图1所示的风险传递UR-GERT的基本构成单元。
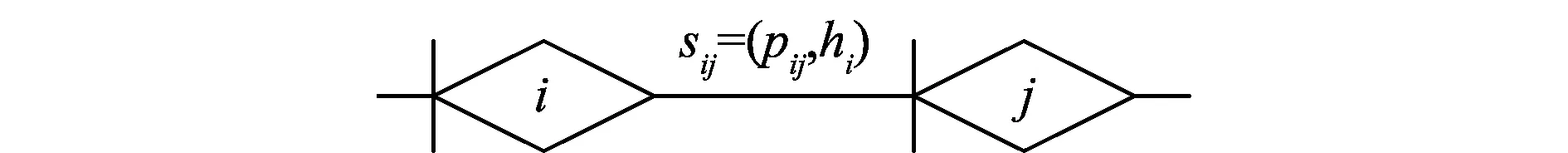
图1 UR-GERT结构模型
Fig.1 Structure model of UR-GERT
构建风险传递UR-GERT模型的步骤如下:
步骤1根据复杂装备系统的不同任务活动,识别出可能出现的事故场景;
步骤2在事故场景中识别风险基元,同时区分风险基元类型,明确网络的节点;
步骤3分析各风险基元间串联、并联等逻辑关系,明确网络的边;
步骤4收集风险基元和风险传递强度等数据,明确网络的流,绘制UR-GERT网络图。
定义5风险度。描述复杂装备系统对于完成任务产生影响的可能性程度称为风险度。风险度根据系统的组成可分为基元风险度和系统风险度;根据风险度不同的刻画方法可分为不确定型风险度和随机型风险度。
定义6[9]风险传递UR-GERT网络的矩母函数和传递系数。如果复杂装备系统风险基元vi的风险度hi∈R,那么,称
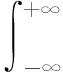
(9)
为风险基元vi风险度hi的矩母函数;
称
Wij(θ,hi)=pijMvi(θ,hi)
(10)
为风险基元vi→vj的传递系数。
性质1不确定随机变量的矩母函数可以生成该变量的各阶原点矩。
证明
证毕
性质2不同的不确定随机矩母函数对应于不同的正则机会分布。
注释5不确定变量的矩母函数计算公式为

(11)
注释6[9]随机变量的矩母函数计算公式为

(12)
定义7UR-GERT网络的等价传导强度和等价矩母函数。
称风险传递UR-GERT模型的等价传导强度为
pE=WE(θ)|θ=0
(13)
称风险传递UR-GERT模型的等价矩母函数为
(14)
定义8[22]复杂装备系统风险度。复杂装备风险传递UR-GERT网络的风险度,复杂装备系统风险度为
(15)
其中
(16)
(17)
注释7基元风险度h既包括概率型风险度hω1,hω2,…,hωm,也包括不确定型风险度hγ1,hγ2,…,hγn,那么系统风险度HE为不确定随机变量。
HE=f(hω1,hω2,…,hωm,hγ1,hγ2,…,hγn)
(18)
系统风险度为不确定随机变量,由系统风险度推导出的等价矩母函数和等价传导强度也是不确定随机变量,由此构建的网络模型为UR-GERT模型。
定义9风险基元重要度。基元风险度的改变导致系统风险度HE改变的程度,称复杂装备活动中风险基元vi重要度为
Ii(t)=HE(1i,h(t))-HE(0i,h(t))
(19)
式中,HE(1i,h(t))、HE(0i,h(t))分别为复杂装备在t时刻风险vi传递和不传递时的系统风险度。
3 风险传递UR-GERT模型求解
3.1 计算风险传递强度
复杂装备系统执行不同的任务活动,事故场景中的风险基元相互作用和影响,风险传递UR-GERT模型中的风险流随之发生变化,当风险度超过风险阈值,复杂装备系统就会出现事故。利用复杂装备系统风险传递强度pij描述风险基元vi对风险基元vj的影响程度。此处主要考虑风险基元间的相互影响,暂不考虑风险基元的风险变化直接对整个系统风险度的影响。根据定义可知,pij越大,相应的风险基元的风险传递能力就越强。
定义10[22]风险传递强度。如果复杂装备风险基元vi与vj的功效系数分别表示为Ui、Uj,那么,称风险传递模型的风险传递强度为
(20)
其中
式中,αi,βi表示复杂装备系统风险基元vi的风险度hi样本的边界值。
3.2 不确定型风险度的矩母函数求解
本文使用矩估计法依据专家的经验数据来确定hi的不确定分布。假设收集数据可以得到一系列专家经验数据即
(x1,α1),(x2,α2),…,(xm,αm)
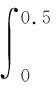
式中,经验数据满足0≤x1 假设该不确定变量服从如下不确定分布为 Φ(x|θ1,θ2,…,θm) (21) 式中,当满足k=1,2,…,m时有 在风险分析中较为常见的是线性不确定分布和之字形不确定分布,因此本文以这两种分布为例进行讨论,线性不确定分布L(a,b)和之字形不确定分布Z(a,b,c)如式(22)和式(23)所示。在求解出未知数得到风险度不确定分布的基础上可以计算风险度对应的矩母函数。 线性不确定分布L(a,b)的分布为 (22) 之字形不确定分布的分布函数为 (23) 定理3如果不确定变量hi服从线性不确定分布L(a,b),那么它的矩母函数表示为 (24) 证明 线性不确定分布相应的逆分布为 (25) 对应的矩母函数为 (26) 证毕 定理4如果不确定变量hi服从之字形不确定分布Z(a,b,c),那么它的矩母函数表示为 (27) 证明 之字形不确定分布相应的逆分布为 (28) 对应的矩母函数为 (29) 假设随机型风险度概率密度函数为f(hi),那么,根据极大熵准则构建的模型为 (30) (31) (32) 量子菌群算法[23]将量子理论引入菌群算法(bacterial foraging optimization algorithm,QBFO),有很强的随机性和全局搜索能力。但是固定的旋转相位不利于算法收敛,因此引入如式(33)所示的自适应旋转角,利用改进QBFO(improved QBFO,NAQBFO)进行求解。 (33) 式中,θmax、θmin表示的是旋转角的最值;θ0表示的是目前最优细菌在单位圆上的角度;θi表示的是目前细菌在单位圆上的角度;C表示的是|θ0-θi|最大值;n表示的是线性指数;m表示的是非线性指数。 算法流程具体如下: 步骤1初始化参数。量子种群的数量N,繁殖的次数Nre,量子趋化的次数Nc,量子迁徙的次数Ned,量子迁徙的概率Ped,量子初始种群Q(t)和旋转角θ; 步骤2测量Q(t)产生二进制解集P(t),评估适应度,得到最佳适应度值为下一目标; 步骤3趋化操作。利用量子旋转门对种群Q(t)更新,测量Q(t)产生二进制解集P(t),评估适应度,得到最佳适应度值为下一目标; 步骤4繁殖操作。对适应度的数值进行降序方式排序,剔去排序差的一半,复制排序好的一半,保证总数不变。 步骤5迁徙操作。随机产生概率Prand,若是Prand 步骤6达到收敛精度或最大迭代次数,输出最佳个体和适应度,算法结束,否则继续。 本文以某型战机眼镜蛇机动[24-25]为例,进行风险传递UR-GERT模型的分析。 眼镜蛇机动的事故场景有3个:一是飞机机动前,大气数据计算机发生故障,战机状态超出进入条件的限制,战机进入复杂状态,影响飞行安全;二是战机具备进入条件,机动时,飞行员对战机状态误判导致操作失误,影响飞行安全;三是飞行员虽然及时准确操纵战机,但是战机机械操纵系统故障或战机“双发”故障,影响飞行安全。 通过事故场景的分析可见,眼镜蛇机动的风险基元有大气计算机故障、电传操纵系统和迎角限制器电门故障、机械操纵系统故障、双发故障、飞行员处置不当,对应的风险度分别记为h1、h2、h3、h4、h5。假设部件或系统累积使用ta小时的故障率为λ(ta),该变量服从三参数Weibull分布。飞行员处置不当的影响因素复杂,无法获取足量的样本数据,只能借助相关领域专家对事件发生的信度进行估计,因飞行员的处置不当引起的风险度h5的分布可以通过矩估计法进行计算。 分析各风险基元间的逻辑关系,建立如图2的战机眼镜蛇机动科目风险传递UR-GERT模型。风险基元1~7分别表示起始节点、大气计算机故障、电传操纵系统和迎角限制器电门故障、飞行员不当处置、机械操纵系统故障、“双发”故障、结束节点。 图2 风险传递UR-GERT模型Fig.2 Model of risk transfer UR-GERT 根据某型07号飞机2002-2012年期间该科目训练数据样本,分别计算相应的h1、h2、h3、h4,本文以大气计算机的风险度h1为例,提供的样本数据如表1所示,优化曲线如图3所示。 图3 优化曲线Fig.3 Curve of optimal 表1 战机眼镜蛇机动危险度样本Table 1 Risk sample of aircraft Cobra maneuver 利用QBFO、遗传算法(genetic algorithm,GA)、NAQBFO同时求解该问题,得到迭代200次的对比图,算法性能比较如表2所示。 表2 算法比较Table 2 Comparison of algorithms 通过比较可知,NAQBFO算法的收敛速度最快,精度最高;QBFO相比GA算法精度更高,可见,NAQBFO算法的改进是有效的。 根据以上数据,利用极大熵模型可以得到概率型风险基元的风险度h1的概率密度函数,即 f(h1)=exp(-3.786-0.256x-0.158x2+0.089x3) 同理,可以得到其他概率密度函数为 f(h2)=exp(-2.895+0.651x-0.442x2+0.102x3) f(h3)=exp(5.965-0.856x+0.692x2+0.025x3) f(h4)=exp(-3.011-0.062x-0.602x2+0.009x3) 邀请部队专家针对飞行员处置不当对飞行安全的影响进行评价,经过讨论研究,专家依10%的信度认为飞行员处置不当对飞行安全的影响为0.12,专家依50%的信度认为飞行员处置不当对飞行安全的影响为0.58,专家依100%的信度认为飞行员处置不当对飞行安全的影响为0.89,由此可以得到飞行员处置不当对飞行安全影响的经验分布曲线如图4所示,得到该变量的不确定分布为 图4 经验数据曲线Fig.4 Curve of empirical data 利用式(20)和表1数据,可以得到(p23,p24,p34)=(0.004 98,0.003 65,0.006 10)。此外,1→2,1→3都表示战机准备进入眼镜蛇机动科目,该活动一定能实现,即p12=p13=1;案例给定p43=0.78,p45=0.22; 5→7表示机械系统故障导致飞机出现非指令机动,根据部队训练数据可得p56=0.024 5。 根据式(9)和式(10),得到各风险基元的风险传递系数wij。由图2的风险基元传递关系和梅森公式,得到UR-GERT网络等效传递系数为 根据式(15),得到眼镜蛇机动科目的总风险度为HE=1.481×10-7,进一步评估可以得到复杂装备系统总风险度的趋势图,在趋势图中通过设定临界风险点,可对任务的风险度进行预警。 计算风险基元重要度:I2=0.561,I3=0.351,I4=0.475,I5=0.018,I6=0.005。I2>I4>I3>I5>I6,表明在该任务中,大气计算机故障对任务安全完成的影响最大,飞行员处置水平和电传操纵系统电门、迎角限制器电门故障对任务安全完成的影响次之,机械操纵系统故障对任务安全完成的影响相对较小。 根据复杂装备系统在执行任务过程中存在多种不同类型风险的特点,基于机会理论构建了UR-GERT模型,对不同类型的风险采取对应的方法进行描述。定义了风险度和不确定随机矩母函数,推导了常见情形下矩母函数的解析表达式,给出了系统风险度、基元风险度、风险基元重要度等概念,旨在解决复杂装备系统执行任务中风险传递关系的建模与风险的定量评价问题,进一步揭示复杂装备系统的风险机理。 但文中需要进一步改进,本文主要研究了单传递参量风险传递模型,具体以退化后的不确定随机变量进行分析。应该继续研究多传递参量风险传递模型,对未退化的不确定随机变量进行分析同时考虑其他不确定分布的变量以进行更复杂的风险分析。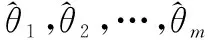
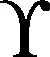
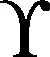
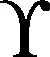





3.3 随机型风险度的概率密度函数


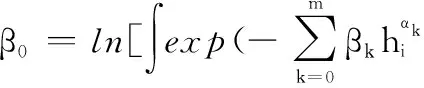
4 案例分析
4.1 事故场景的描述
4.2 装备风险基元分析
4.3 风险传递UR-GERT模型





5 结 论
