冶金加热过程数学模型及其参数优化研究

冯国勇

（兰州资源环境职业技术学院，甘肃 兰州730021）

随着科学技术的不断发展，冶金行业也发生了改变，工艺逐渐从简单走向了复杂，更具科学性。现代冶金行业包含了金属学、热力学以及动能学等多方面知识。在整个冶金加热过程中，这种知识受到广泛应用。事实上，冶金工作是十分复杂的，操作过程具有一定的局限性。冶金过程中会用到冶金炉，冶金炉中发生大量的物理与化学反应，多种形态的金属同时出现[1]。在整个冶金加热过程中，冶金炉是封闭的，相关工作人员需要通过冶金炉外部的仪表盘进行操作，并根据参数对冶金情况进行分析，利用仪表中显示的数据进行计算。并建立相应的数学模型，便于得出结论，对冶金工作进行进一步指导。近年来，计算机技术发展迅猛，逐渐应用在各个行业中，冶金加热过程中，计算机技术为数学模型的建立提供了有力基础，使工作者可以通过模型对冶金过程进行控制，获得了突破性的发展[2]。对多种金属矿产资源的冶炼加热过程进行分析，研究数学模型使用及其参数优化的过程。经验与机理结合在一起，属于混合型模型，这种数学模型的建立通常需要相关工作者根据自身的实践经验对相应工艺进行推理与假设，形成具体的方程。建立后，再将多种参数带入其中，对方程进行验证。第三种模型属于统计模型，全部依靠操作者的工作经验，不对具体原理与理论进行分析，在参数的变化过程中总结规律，这种类型的数学模型，虽然较为方便，但是准确程度并不高。这三种数学模型都是在冶金加热过程中较为常见。本文冶金加热过程数学模型相关组成数据如表1所示。

表1 模型组成

1 探究冶金加热过程数学模型及其参数优化方式

在冶金加热过程中，数学模型的建立有以下几种类型，第一个类型用于较为简单的问题，在模型建立前，需要对工业过程进行准确了解，总结其中的规律，结合理论进行具体分析，在相应的方程中能够体现工作性质与行为，这种模型建立为机理模型。将机理模型应用到冶金加热的过程中，能够总结出各个参数的具体变化情况。在使用这种数学模型时应注意掌握冶金工作的原理与规律。第二种模型将操作者的

由表1所示，冶金加热过程中数学模型的建立就是对冶金原理与冶金设备进行分析的过程，对其中的多种物理化学反应进行研究。数学模型能够对冶金理论进行传输，这也是一切工作的基础，模型能够对坐标、方程式等参数进行统计。使整个冶金加热过程更加细化，在机理模型的基础上，将操作者的经验融入其中，并进行计算。在模型建立与计算中需要依靠计算机设备与先进的计算机技术，研究各项参数的变化，总结其中规律，实现对冶金加热过程中各个参数进行优化的目的。数学模型与相应参数不断优化的过程中，也能够寻找出最好的冶金加热方案，在各种环境下都能够进行冶金作业。选取一组参数值，并通过数学模型将参数进行优化。在优化过程中相应方程能够对整个空间的信息与数据进行搜索，并完成相应的组合，形成多项式。对智能优化方法进行分析，判断冶金加热过程中粒子的变化情况，分析粒子之间的关系，将整个空间视为一个整体，每一个粒子都是独立的个体，对粒子群进行优化，公式如下。

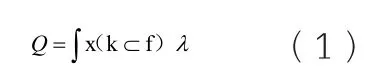
式中：x 为微粒值，k 为当前代数值，λ为加速常数，f为学习因子。冶金加热模型通过多次参数代入，得到的结果都是相对于最初更加优化的，但同时也具有一定的局限性。通过适当改进后实现参数最优，其运行效率也明显得到了提升，可见在这一方程下的数学模型有着较好的效果。

2 实验结果与分析

为证明冶金加热过程数学模型及其参数优化效果，完善系统模型。进行进一步实验，实验为对照实验，将传统数学模型和参数优化方式与本文提出的模型和方式进行比较，使用多种数据采集，分别利用这两种方法对冶金过程中耗费率进行检测，对比结果如图1所示。

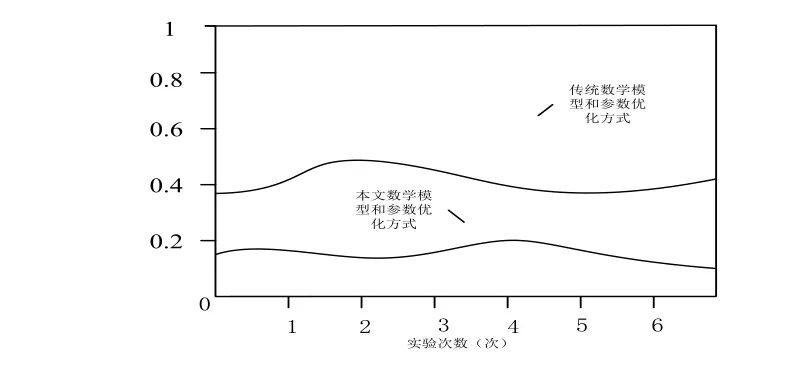
图1 实验对比图

根据图1实验对比图可以看出，本文提出的数学模型及其参数优化方式相比于传统数学模型和参数优化方式能够有效降低冶金过程中的消耗率，有效、清晰的获取工艺过程中各参数的变化规律及参数间的定量关系，通过变化规律实现对冶金加热过程中消耗量的控制，节约能源，具有较好的应用价值。

3 结语

冶金加热中应用到了多种学科的知识，数学模型的建立过程中也出现了许多方程组，这些方程组能够对参数进行优化，并记录其变化的规律。建立数学模型对参数进行优化能够使冶金加热工作具有更高的效率与质量。通过对模拟数值的分析，能够使工作者对冶金加热的过程更加了解，对相关工艺的完善起到了重要的作用。冶金加热过程中数学模型的建立与参数优化取得了良好的效果，发展过程从简单到复杂，由一维到多维，实现了真正的动态研究，但仍然存在许多不足之处，参数优化效果仍然没有达到最佳，相关技术工作者还应在实践过程中对数学模型进行完善，以促进冶金行业的持续发展。