基于K中心点聚类分析的大地电磁阻抗识别

赵 玄，严家斌,2*，皇祥宇,2，胡 涛

(1.中南大学 地球科学与信息物理学院，湖南 长沙 410083； 2.中南大学 有色资源与地质灾害探查湖南省重点实验室，湖南 长沙 410083)

0 引 言

大地电磁法(MT)诞生于20世纪50年代初，该方法具有工作效率高、成本低廉、勘探深度大、高阻层的屏蔽作用小等特点[1-2]，广泛应用于矿产勘查、地下水与地热勘探、油气普查等方面，产生了巨大的经济效益[3-5]。随着城市的扩展和人类工业活动的加剧，大地电磁场信号的观测越来越困难，干扰越来越严重，从受干扰的观测数据中估计稳定的阻抗或视电阻率是当前地球物理电磁信号处理的难点之一。Sims等较早提出依据最小二乘法的张量阻抗估计，该方法要求各数据道之间的噪声相互独立，但当电磁资料存在相关噪声以及观测误差不服从高斯分布规律时，由最小二乘法估算的阻抗会产生严重偏差[6]。为了克服上述问题，Egbert等将稳健性估计(Robust Estimation)引入到地磁转换函数中，并详细介绍了加权最小二乘法和改进算法[7]。为了进一步进行稳健性估计，Chave等详细介绍了地球物理中几个重要的物理量：功率谱、相干度和转换函数，并综述了Robust估计理论，从统计学原理出发梳理了M估计和极大似然估计法[8]。针对海洋环境下的大地电磁法，柳建新等提出了基于相关归一Robust法，根据相关系数的变化改进Robust法的权系数[9]。张刚等将基于重复中位数估计的Robust法应用于长周期大地电磁阻抗张量估算中[10]。Chave等提出了基于Stable分布的最大似然阻抗估计法，根据数据自身的噪声分布进行加权，能更合理地给出阻抗估计值[11-12]。常规的阻抗估计法对噪声辨识度很低，未利用大地电磁阻抗的物理特性分辨高质量数据，导致噪声严重干扰信号数据，使得阻抗结果发生严重偏差。由于大地电磁数据中高质量信号数据不能有效利用，所以聚类分析算法被引入电磁数据处理中。李晋等介绍了基于递归分析和聚类分析的大地电磁信噪辨识及分离方法[13]，该方法虽然保留了大地电磁信号低频段的缓慢变化信息，改善了低频段大地电磁数据质量，但对电场和磁场的处理是独立进行的，对电磁场的分量间相关性考虑不足。

本文从大地电磁阻抗的实虚分量特性出发，通过定义阻抗的欧式距离构建阻抗相似性度量，利用其相似性对受干扰阻抗、轻微受干扰阻抗、未受干扰阻抗进行K中心点聚类分析，识别出高质量的信号，并基于仿真实验和实例分析验证该方法的有效性。

1 原 理

聚类分析(Clustering Analysis)是数据挖掘的主要方法之一[14-17]，主要研究数据之间的相关性，这种相关性大小是通过一定的相似性准则来判断的，然后依此将对象分簇或聚类。在频率域内针对某一地质构造，高质量的大地电磁信号数据的阻抗实虚分量必然在真实阻抗附近浮动，其阻抗间存在相似性，而与噪声数据阻抗间存在差异性[18]。这一特性十分适合采用聚类分析进行阻抗数据的优选，筛选出高质量的数据。采用聚类分析的结果使得信号数据尽可能归为一类，信号数据和噪声归为不同类。

1.1 相似性度量

一个聚类分析过程的质量取决于对度量标准的选择。为了度量数据对象之间的相似或者接近程度，需要定义一些相似性度量标准。聚类分析中，为了表示两个数据对象之间的相似度，一般采用特征空间中的距离作为度量标准来计算两个样本间的相异度[16-17]。为了描述阻抗数据之间的相似或者接近程度，提出了阻抗(Z)的欧式距离。其表达式为

(1)

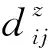
由式(1)可知，欧式距离越小表示高质量阻抗之间的相似或接近程度越大。相对于受噪声干扰的数据，受干扰较小的信号数据的阻抗欧式距离小。

1.2 K中心点聚类分析

K中心点(K-medoids)聚类分析是为了降低K-means算法[19]对噪声孤立点的敏感度而提出的新算法。K中心点聚类分析选择类或簇中最靠近均值中心点的一个对象来代表该类或簇的中心点，可以有效消除孤立点对聚类效果的影响[20]。在聚类分析中只需要计算类或簇的中心点，并选择该类或簇内靠近中心点的对象作为新中心点，依次循环迭代，直到得到稳定的类中心[21]。

以频率域阻抗为例，对于包含N个阻抗数据对象的集合X，随机选取K个数据对象作为初始聚类中心点，并把K个初始聚类中心点表示成K个初始类。计算集合内所有数据对象与各个初始聚类中心点的阻抗欧式距离，依据就近分配原则，将数据对象划分到最靠近的类内，重新分配每个数据对象直至所有数据对象分配完毕，计算新的聚类中心点。K中心点聚类分析步骤为：①输入K，X=[ReZ,ImZ]；②选择K个初始聚类中心点，C[1]=X[1]，C[2]=X[2]，…，C[K]=X[K]；③计算第i个类X[i]与第②步中K个初始聚类中心点的阻抗欧式距离，找到离它最近中心点C[m]，将其分配到C[m]所在的类内，并对该点作标记；④计算出m个类内的所有数据对象均值，选择靠近均值的数据对象作为m个类的新中心点；⑤重复第③、④步，直至所有数据分配到类内以及达到设定迭代次数。

1.3 类的选取准则

经过K中心点聚类分析后，每个频点下的阻抗数据被划分为K个类。把每个类的中心点作为该类阻抗的代表值，每个频点下将会得到K个阻抗值和对应的视电阻率。从K个结果中挑选出最佳阻抗值，依据电磁法理论定义类的选取准则。

(1)相干度准则。相干度可以衡量输入信号和输出信号的相关性，相干度越大，数据相关性越好，信号质量越好。因此，设定相干度阈值，筛选出满足阈值对应的类。

(2)紧凑性准则。为了描述数据聚集程度，提出了紧凑性概念。以某一频点下的阻抗为例，对于包含N个阻抗数据对象的集合X={X1,X2,…,XN}，X=[ReZ,ImZ]，假设数据集合X被划分为K个类，每个类中数据对象个数为{n1,n2,…,nk}，且n1+n2+…+nk=N。以第j类为例，该类的紧凑性Cj(f)表达式为

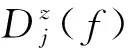
紧凑性Cj(f)值越小，说明类内数据对象聚集的越紧凑，数据之间相似程度越高，更符合高质量信号数据的阻抗高相似性特征，紧凑性好的类被认为是高质量信号数据所在的类。满足相干度准则的条件下，选择紧凑性好的类[22]。

1.4 算法步骤

算法步骤为：①分别对M段时间域数据采用最小二乘法求取初始阻抗值，得到每个频点下M个阻抗值；②输入K，X=[ReZ,ImZ]，对第①步中阻抗组成的集合X采用K中心点聚类分析，每个频点下的阻抗被划分到K个类内；③计算每个频点下各类的相干度和紧凑性；④依据相干度准则和紧凑性准则，筛选出符合要求的类以及相对应的阻抗值；⑤根据第④步中的阻抗值计算出相对应的视电阻率。

2 仿真实验

大地电磁资料中存在着多种噪声，使得数据处理异常困难，常规方法估算的结果会发生偏移[23-24]。通过在大地电磁仿真数据中加入噪声，模拟实际情况下噪声对信号的影响，并对比基于K中心点聚类分析和Robust法的估算结果。首先利用蒙特卡罗(Monte Carlo)法产生互不相关的随机时间序列，作为电道或者磁道数据，通过傅里叶变换把时间域序列转化到频率域，根据层状介质的视电阻率理论公式，加入设定的电性模型参数，计算出磁道或者电道频率域数据，再通过傅里叶反变换转换到时间域。本文设定的电性模型参数为：地下结构为两层均匀介质，第一层介质电阻率为500 Ω·m，厚度为250 m，第二层介质电阻率为100 Ω·m。上述仿真实验产生了x方向电道分量Ex和y方向电道分量Ey各50段，x方向磁道分量Hx和y方向磁道分量Hy各50段，各段数据采样长度为2 048，采样频率为10 000 Hz。在大地电磁仿真实验的电道或者磁道中加入类三角波噪声和脉冲噪声。

图1 原始磁场和加噪声后磁场的时间序列Fig.1 Time Series of Magnetic Field with and Without Noise

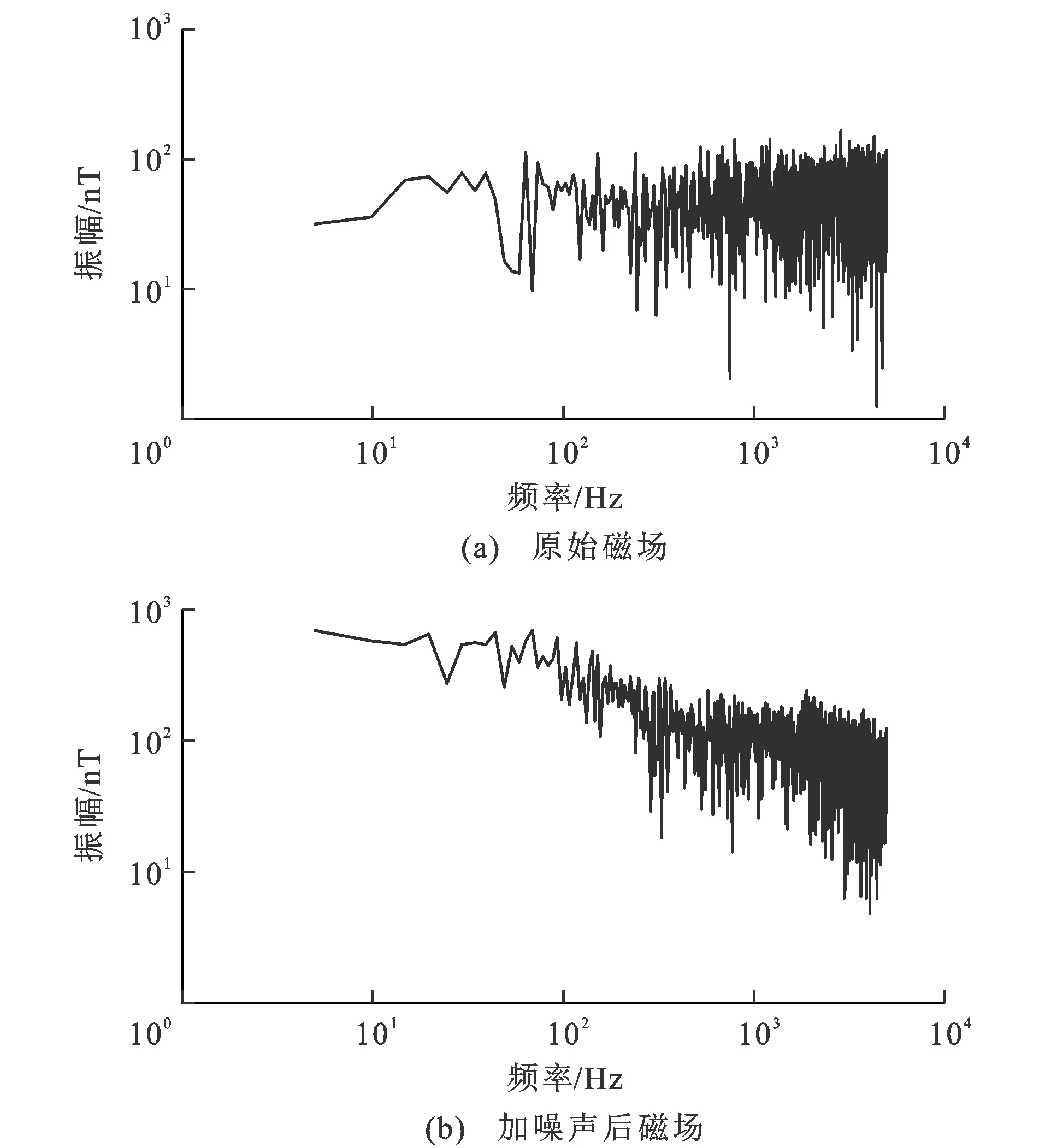
图2 原始磁场和加噪声后磁场的频谱Fig.2 Frequency Spectra of Magnetic Field with and Without Noise

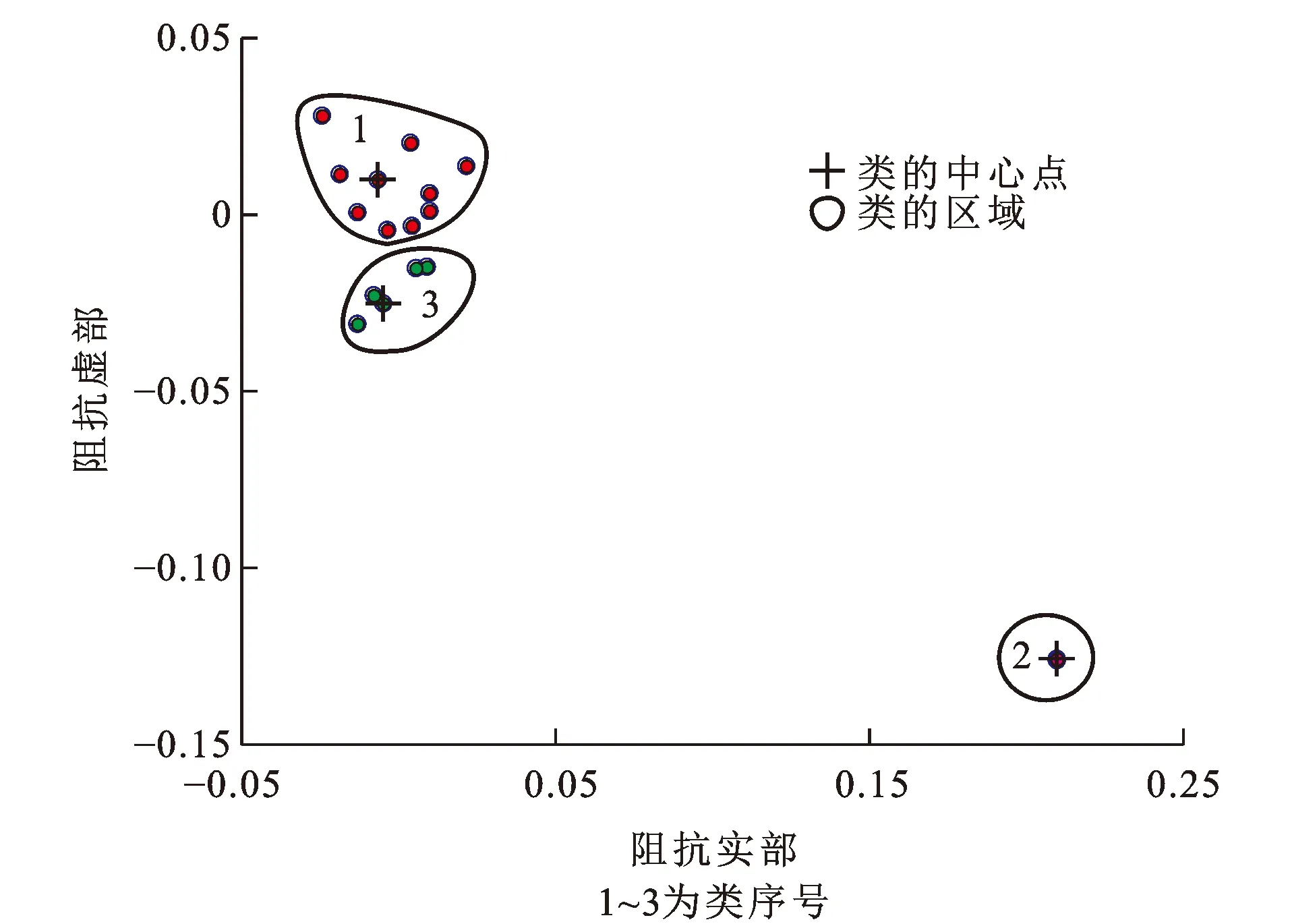
图3 磁场噪声阻抗聚类图(f=24.41 Hz)Fig.3 Clustering Diagram of Impedance of Magnetic Field with Noise (f=24.41 Hz)

(1)随机选出15段磁道仿真数据，在选择的数据段不同位置加入类三角波噪声、脉冲噪声。信号与类三角波噪声幅值之比为1∶4，噪声数据长度占每段数据总长度的10%；信号与脉冲噪声幅值之比为1∶50。对50段数据分别采用Robust法和K中心点聚类分析估计视电阻率和相位。由图1(a)和图2(a)可知，不含噪声的磁场频谱能量是逐渐增大的。在磁场中加入类三角波噪声和脉冲噪声[图1(b)]，这两种噪声影响所有频点的磁场频谱[图2(b)]，使得频谱能量明显高于原始信号能量。对上述50段数据先进行K中心点聚类分析，对分类后的阻抗按照相干度准则和紧凑性准则筛选出最佳阻抗值所在的类，计算最佳阻抗值所对应的视电阻率和相位。以24.41 Hz频点为例，阻抗数据被划分到3个区域内(图3)。表1是该频点下划分成3个类对应的参数，由于第3类的相干度和紧凑性很好，所以选择第3类为最佳类，并计算最佳类所对应的视电阻率及相位。对其他频点采用相同计算方法，得到视电阻率曲线(图4)和相位曲线(图5)。从图4、5可以看到，基于K中心点聚类分析估算的结果更接近理论曲线，当频率高于1 000 Hz时，基于Robust法估算的视电阻率小于理论值。相对于Robust法，基于K中心点聚类分析可以分离和识别出高质量数据对应的阻抗，削弱了噪声的干扰，使结果更为可靠。

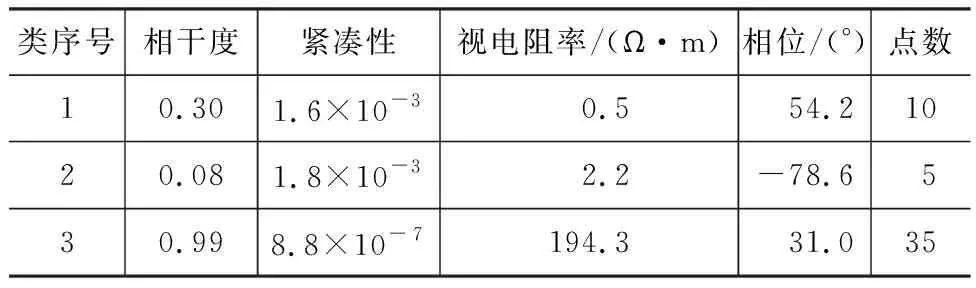
表1 基于K中心点聚类分析的磁场阻抗识别评价参数(f=24.41 Hz)Tab.1 Evaluation Parameters of Impedance Recognition for Magnetic Field Based on K-medoids Clustering Analysis (f=24.41 Hz)

注：理论上，视电阻率为194.3 Ω·m，相位为31.0°。

图4 磁场噪声视电阻率曲线Fig.4 Apparent Resistivity Curves of Magnetic Field with Noise

图5 磁场噪声相位曲线Fig.5 Phase Curves of Magnetic Field with Noise

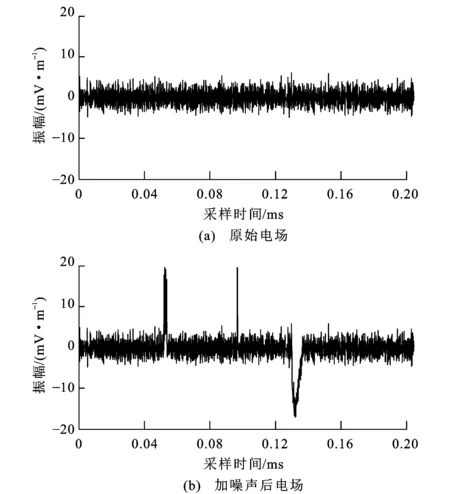
图6 原始电场和加噪声后电场的时间序列Fig.6 Time Series of Electric Field with and Without Noise

(2)随机选出10段电道仿真数据，在选择数据段的不同位置加入类三角波噪声、脉冲噪声。信号与类三角波噪声幅值之比为1∶4，噪声数据长度占每段数据总长度的10%；信号与脉冲噪声幅值之比为1∶50。对50段数据分别采用Robust法和K中心点聚类分析估计视电阻率和相位。由图6(a)和图7(a)可知，不含噪声的电场频谱能量是逐渐增大的。在电场中加入类三角波噪声和脉冲噪声[图6(b)]，这两种噪声影响所有频点的电场频谱[图7(b)]，使得频谱能量明显高于原始信号能量。对上述50段数据进行K中心点聚类分析，对分类后的阻抗按照相干度准则和紧凑性准则，筛选出最佳阻抗值所在的类，并计算其对应的视电阻率和相位。以43.95 Hz频点为例，阻抗数据被划分到4个区域内(图8)。表2是该频点下划分成4个类分别对应的参数，第2类的相干度和紧凑性很好，选择第2类作为最佳类，并计算其对应视电阻率和相位。对其他频点采用相同计算方法，得到视电阻率曲线(图9)和相位曲线(图10)，基于K中心点聚类分析的估算结果更接近理论值，而基于Robust法估算的视电阻率曲线和相位曲线都出现了波动，结果偏离了理论值，由此说明基于K中心点聚类分析可以识别和筛选出高质量信号数据的阻抗，进而估算出更为可靠的结果。

图7 原始电场和加噪声后电场的频谱Fig.7 Frequency Spectra of Electric Field with and Without Noise

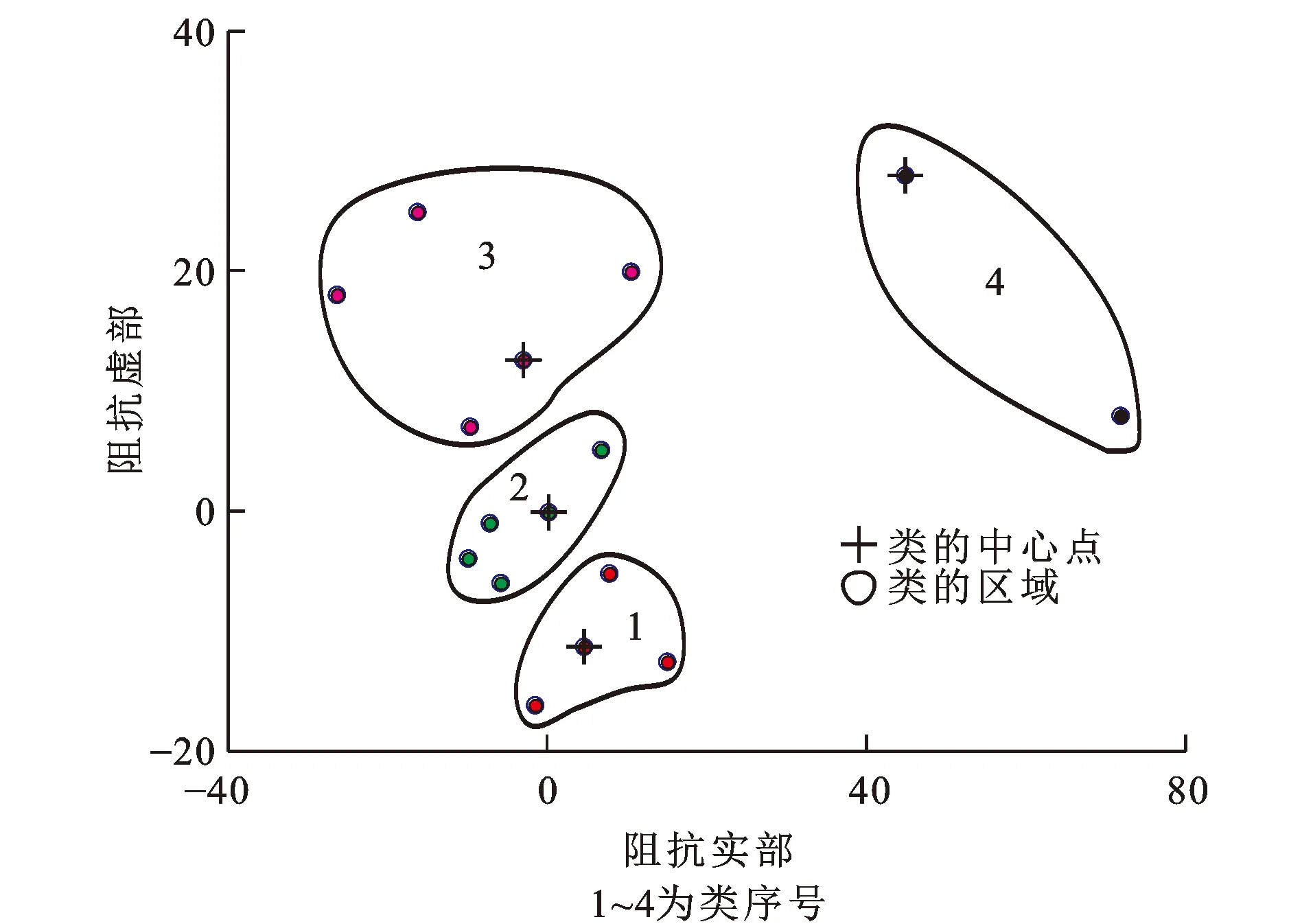
图8 电场噪声阻抗聚类图(f=43.95 Hz)Fig.8 Clustering Diagram of Impedance of Electric Field with Noise (f=43.95 Hz)

类序号相干度紧凑性视电阻率/(Ω·m)相位/(°)点数10.081.60440 000.067.9420.990.02186.130.93930.092.70480 000.076.5540.168.408 100 000.0-32.02

注：理论上，视电阻率为186.1 Ω·m，相位为30.7°。

图9 电场噪声视电阻率曲线Fig.9 Apparent Resistivity Curves of Electric Field with Noise

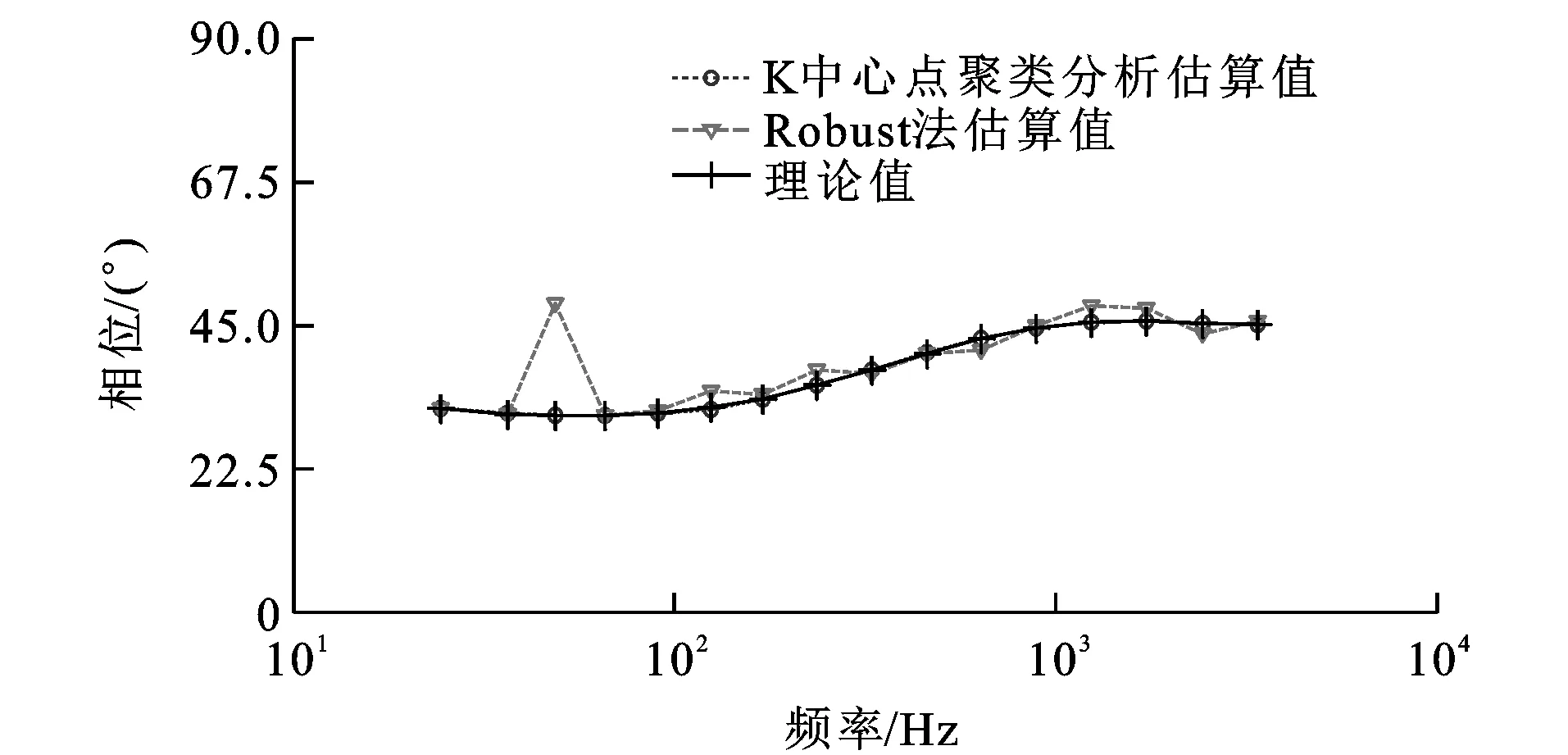
图10 电场噪声相位曲线Fig.10 Phase Curves of Electric Field with Noise

3 实例分析

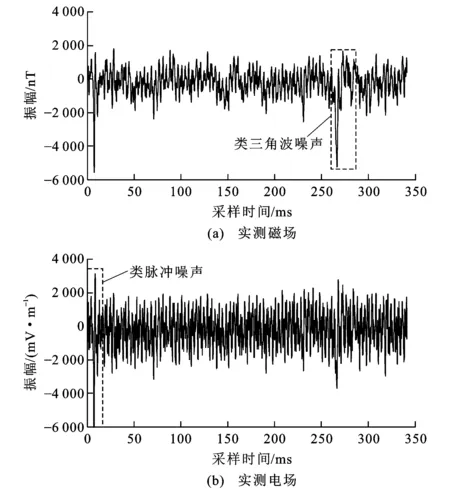
图11 实测磁场和实测电场时间序列Fig.11 Time Series of Measured Magnetic Field and Electric Field

为验证基于K中心点聚类分析的实际应用效果，选取云南省昭通市牛栏江天花板水电站田坝村堆积体处电磁成像系统观测数据进行验证。观测区周围无高压线，但居民较多。图11是采集的原始时间序列数据，磁场在水平轴260～280 ms之间存在似类三角波噪声，电场在水平轴0～20 ms之间存在明显的似类三角波噪声和脉冲噪声。该测点电道和磁道信号中存在明显的类三角波噪声和脉冲噪声(图11)，同时还存在幅度较小的类方波等噪声。由仿真实验可知，不含噪声的电磁数据频谱能量逐渐增大，而测点的频谱能量逐渐减小，说明噪声影响了所有频点的频谱(图12)。对测点数据采用和仿真实验一样的K中心点聚类分析，对阻抗数据进行聚类分析。以频点82.5 Hz为例，该频点下阻抗经过K中心点聚类分析，划分成6个区域(图13)，每个区域代表一个类。由图13可知，第2、3、6类内数据点比较分散，说明类内的阻抗受噪声影响很大，而第1、4、5类内的数据点分布集中，说明高质量数据比较多。由表3可知，第1、4、5类所对应的相干度和紧凑性很好，而第5类所对应的紧凑性最好，因此，选择第5类为最佳类，把其对应的视电阻率作为最终的视电阻率。对其他频点采用相同计算步骤，得到视电阻率曲线(图14)。由图14可知，相对于基于Robust法的估算结果，基于K中心点聚类分析的估算结果更为光滑连续，不会出现异常跳动，更贴近真实地下结构，说明该方法可以识别出高质量数据的阻抗，降低了噪声干扰，使结果更为可信。

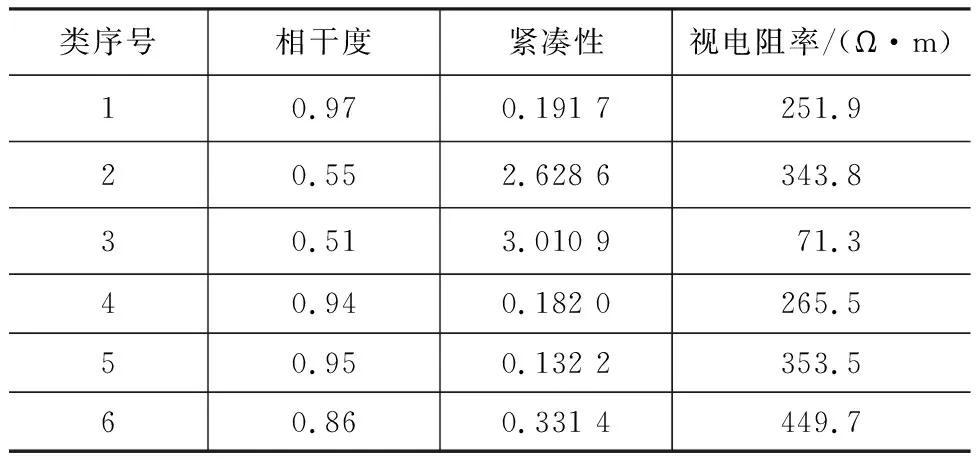
表3 基于K中心点聚类分析的实测阻抗识别评价参数(f=82.5 Hz)Tab.3 Evaluation Parameters of Measured Impedance Recognition Based on K-medoids Clustering Analysis (f=82.5 Hz)

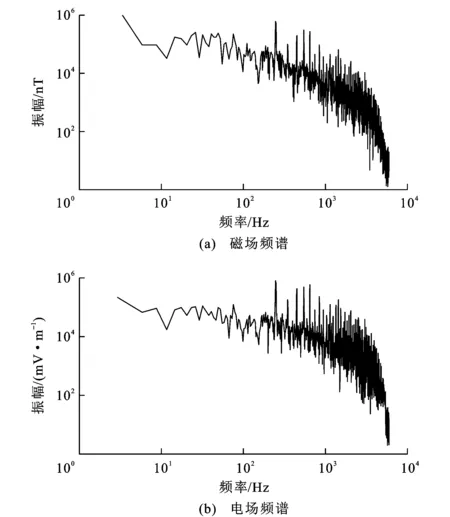
图12 实测磁场和电场频谱Fig.12 Frequency Spectra of Measured Magnetic Field and Electric Field

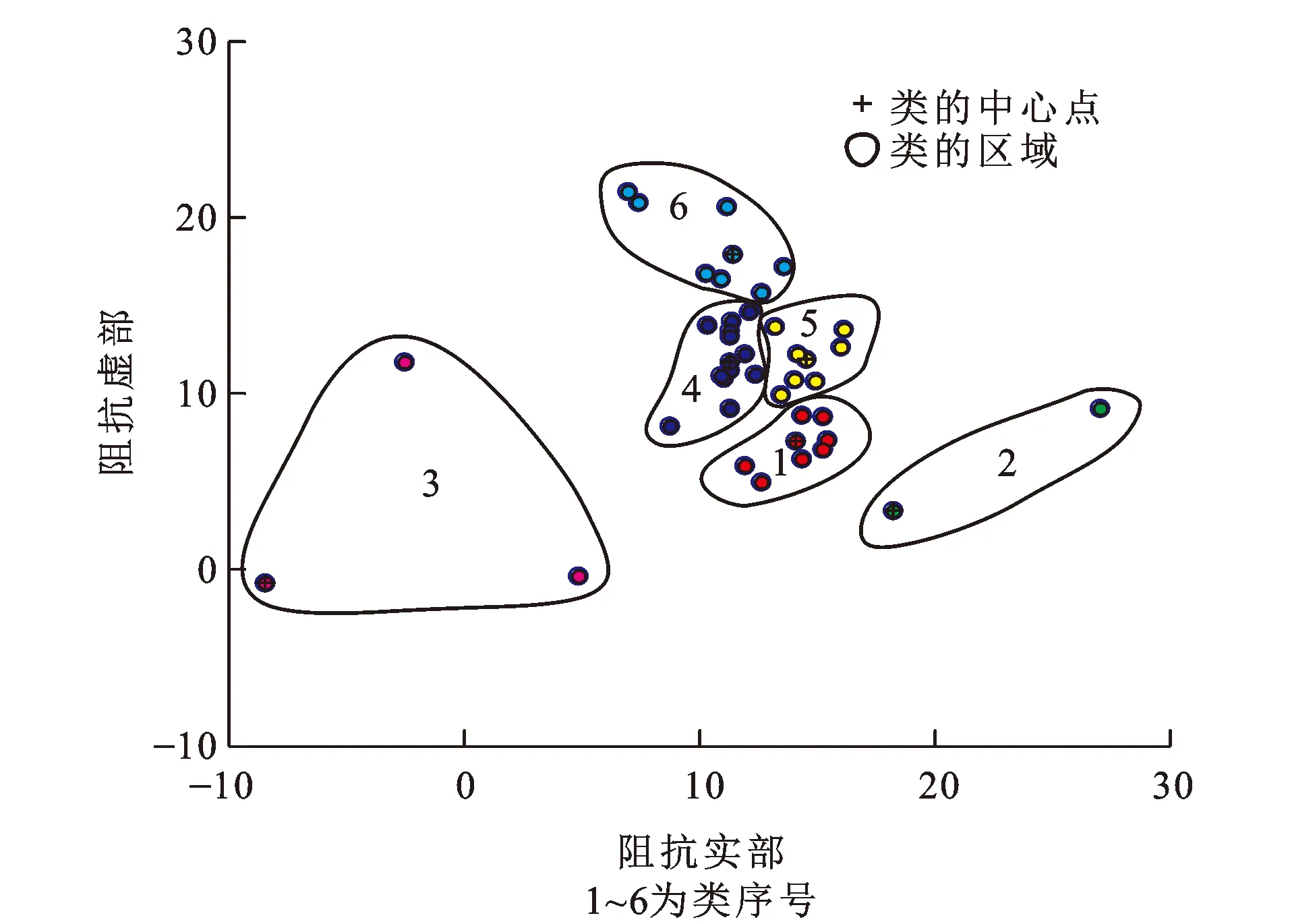
图13 实测数据阻抗聚类图(f=82.5 Hz)Fig.13 Clustering Diagram of Impedance of Measured Data (f=82.5 Hz)

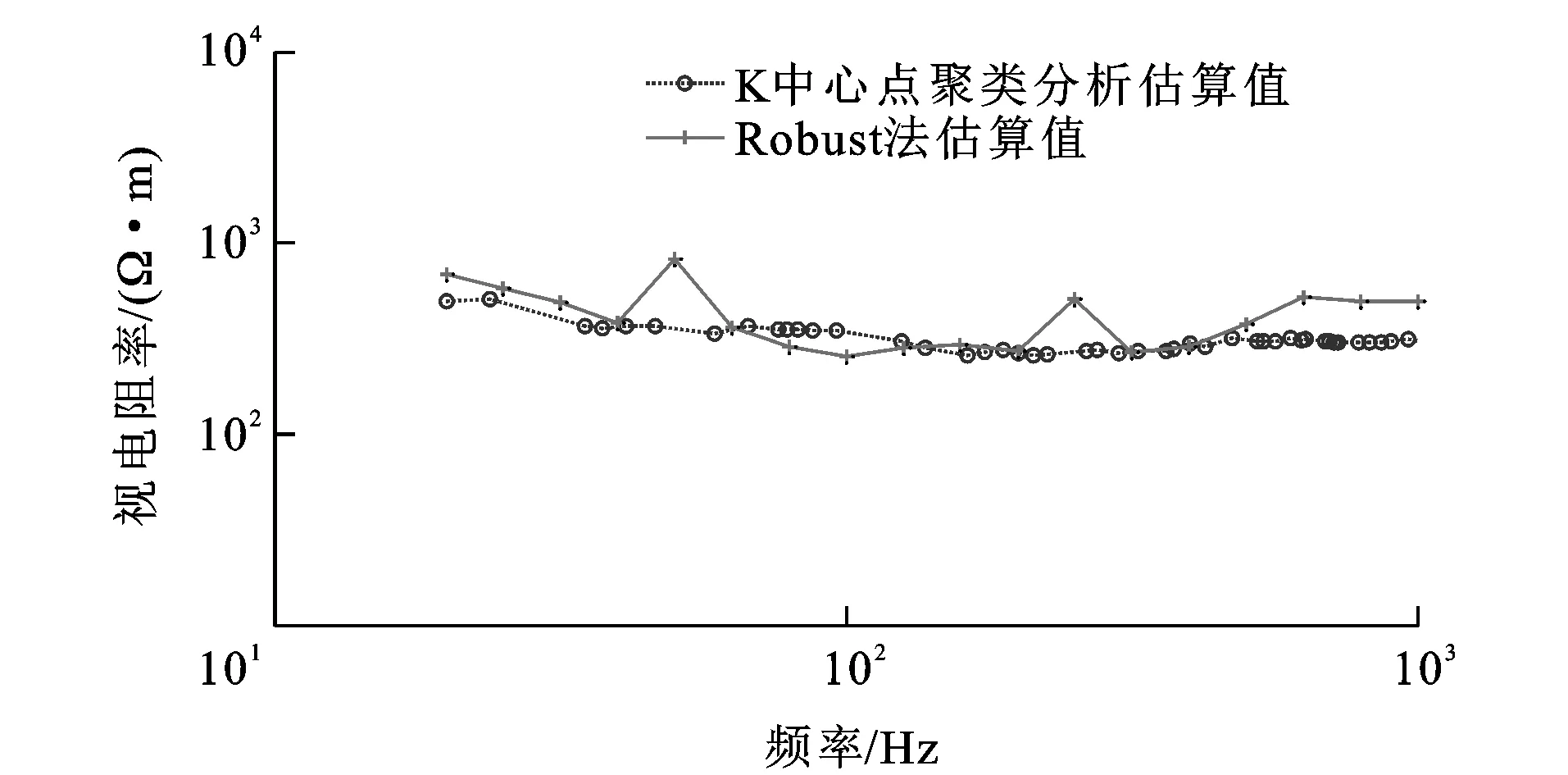
图14 实测数据视电阻率曲线Fig.14 Apparent Resistivity Curves of Measured Data

4 结 语

(1)从大地电磁阻抗的实虚分量特性出发，定义了阻抗欧氏距离，描述阻抗数据之间的相似性，提出了基于K中心点聚类分析的电磁信号识别及阻抗提取方法，并依据类的选取准则，识别出可靠的阻抗值。通过仿真实验和实例分析，基于K中心点聚类分析可以识别并提取出高质量数据的阻抗，得到稳定阻抗值和视电阻率，提高估算的可靠性和稳定性。

(2)Robust法更适用于磁场受干扰小时的情况，当电场或者磁场含有异常幅度大的噪声时，Robust法估算的结果不再稳定，会使结果发生偏差；而K中心点聚类分析是利用阻抗的物理特性，高质量数据的阻抗会集中分布且具有高度的相似性，因此，受影响较小，得到的阻抗更合理有效。由于个别异常点的存在和初始聚类数目的选择都会影响聚类算法效率，所以本文的方法还需要进一步的优化。