土石坝-覆盖层-基岩体系动力相互作用研究
2018-12-07孔宪京邹德高周晨光
余 翔 ,孔宪京 ,邹德高 ,周晨光
(1.大连理工大学 水利工程学院,辽宁 大连 116024;2.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
1 研究背景
随着我国水利水电建设的快速发展,大坝的建设不断增加。其中,由于土石坝适应地理及地质条件能力较强,是我国已建和待建工程中的主要坝型[1-2]。我国西部地区水资源丰富但地震烈度高且地质条件较差,土石坝的建设难以避免地面临强震和坝基覆盖层的双重问题[3-4]。覆盖层上土石坝的抗震设计是确保抗震安全的关键,然而,覆盖层土体多为饱和土且具有动力非线性特性,土石坝-覆盖层-基岩体系动力相互作用复杂,传统方法很难把握大坝地震反应特性。因此,采用合理的动力相互作用分析方法,描述地震时土石坝-覆盖层-基岩的动力相互作用,准确获取覆盖层上土石坝的地震反应,对评价和确保大坝抗震安全至关重要[5]。
有限元法是目前广泛采用的地震反应分析方法。在研究覆盖层上土石坝地震反应时,需人为截取有限的覆盖层范围作为计算区域。在输入地震动时,目前大多采用地震动一致输入方法,即将基岩底部边界固定并在各节点上直接施加地震惯性力,其地震动输入边界处各点的地震反应在同一时刻相同,而且地震波会在边界处发生反射,常常给计算结果带来较大误差[6-7]。地震动波动输入方法[8-11]结合人工边界(黏性边界[12]和黏弹性边界[13]等)和节点等效荷载,可以较好地模拟地震入射波及散射波向无限远域的辐射,在理论上更为严密。地震动波动输入方法在混凝土坝工程[14]、地下工程[15]等结构工程[16-17]动力反应中得到了广泛应用,但在土石坝工程领域仍处于发展阶段[18],研究成果较少。对于覆盖层上的土石坝工程,覆盖层土体在地震作用下呈非线性特性,较难获取施加于覆盖层地基截断边界处的人工边界参数和等效节点荷载。因此,目前鲜有涉及土石坝-覆盖层-基岩体系动力相互作用的研究。
对覆盖层上土石坝进行地震反应分析时,合理的地震动输入方法是描述土石坝-覆盖层-基岩动力相互作用特性的基础,也是准确获取大坝地震反应的关键。目前常用的一致输入方法能否满足计算精度要求、对哪些方面影响较大等是研究者们比较关心的问题。鉴于此,本文研究不同的土石坝-覆盖层-基岩动力相互作用分析方法不同(地震动一致输入方法和非线性波动输入方法)时覆盖层上土石坝的地震反应,并考虑覆盖层厚度、土体动力特性、地震强度及地震波特性等因素的影响,以期为覆盖层上土石坝的抗震设计和安全性评价提供参考。
2 计算分析模型
2.1 分析模型与材料参数 为便于比较分析不同土石坝-覆盖层-基岩动力相互作用分析方法,选取坐落于单一覆盖层土体上的均质堆石坝进行计算,如图1所示。以下文中各计算工况中坝体形状参数保持不变。其中,坝高150 m,坝顶宽14 m,上、下游坝坡坡度均为1∶2。

图1 覆盖层上土石坝地震反应分析模型

表1 静力和动力计算参数
材料参数为某覆盖层上土石坝工程的土料三轴试验结果。首先进行大坝静力填筑过程分析,以获取动力分析的初始状态,其中土体采用E-μ模型模拟,参数见表1。动力反应分析时,土体采用等效线性模型模拟,最大动剪切模量计算参数如表1所示。图2为土体的归一化动剪切模量比及阻尼比与动剪应变的关系曲线。覆盖层底部线弹性基岩的密度ρ=2750 kg/m3,弹性模量E=8 GPa,泊松比μ=0.24。

图2 模量比及阻尼比与动剪应变的关系曲线
当地震动采用一致输入时,在底部截断边界施加地震惯性力,并取D/H=10以消除侧向截断边界的影响。当地震动采用波动输入时,采用非线性波动输入方法,联合自由场非线性动力响应和非线性人工边界模拟分析模型所有截断边界处的地震动。其步骤为:(1)进行覆盖层-基岩体系的二维土柱的自由场非线性动力反应分析;(2)建立土石坝-覆盖层-基岩体系的有限元模型并在截断边界处添加黏性人工边界单元[19];(3)将自由场非线性动力响应过程输入至土石坝-覆盖层-基岩体系的人工边界单元处;(4)黏性人工边界动态获取其依附土体单元的动力参数并计算人工边界参数;(5)根据人工边界参数、边界位置和非线性自由场动力响应结果,计算施加于截断边界上各节点的等效节点荷载,进而开展该时刻的有限元动力分析;(6)重复第(4)步和第(5)步直至最后时刻。
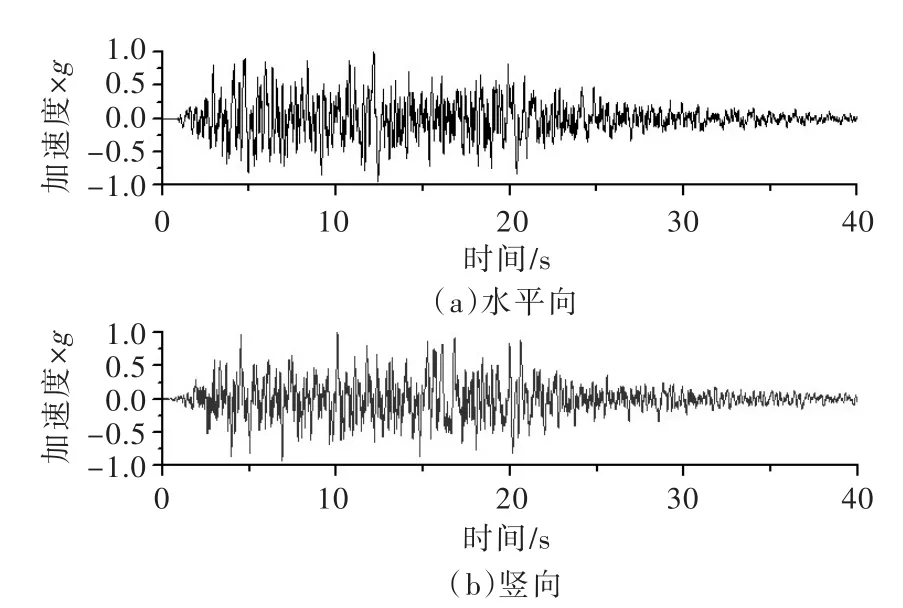
图3 地震波1加速度时程曲线

图4 地震波2加速度时程曲线

图5 地震波3加速度时程曲线

图6 地震波4加速度时程曲线

图7 地震波加速度反应谱

图8 地震波加速度傅立叶谱
2.2 地震动 分别输入4个实际土石坝工程场地地震波,地震波时程曲线见图3—图6。4条地震波的加速度反应谱及傅立叶谱见图7和图8,由图可知,各地震波的主频范围在2~7 Hz之间,但在放大倍数和频率组成方面差别明显。
2.3 计算工况 计算工况如表2所示。各计算工况分别考虑了覆盖层厚度、覆盖层土体特性、地震动强度及地震波频谱特性。其中,地震动强度为工程场地所在地区半无限空间均质岩体在平坦自由地表[20]的水平向加速度峰值,竖向加速度峰值取为水平向的2/3。计算软件为大连理工大学抗震研究所开发的岩土工程非线性有限元分析程序GEODYNA[21]。
3 计算结果与分析
本文主要整理大坝的加速度峰值,结合大坝中部加速度峰值分布及关键位置加速度反应的频谱特性,分析两种地震动输入方法计算结果的差异及规律。

表2 计算工况

表3 不同覆盖层厚度时的大坝加速度反应峰值
3.1 覆盖层厚度 采用地震波1,地震动强度取0.3g,对覆盖层厚度分别为75、150、300和450 m的土石坝进行不同地震动输入方法的地震反应分析。坝基交界中部和坝顶中部(如图1所示)位置的加速度峰值及波动输入方法结果相对一致输入方法结果的降低率列于表3。由表3可知,采用非线性波动输入方法进行地震反应分析时,竖向加速度峰值的降低率明显大于水平向。这是由于坝基覆盖层土体多接近于饱和,较短的地震过程中覆盖层土体基本处于不排水状态,泊松比较大[22],土体压缩模量较高且地震过程中衰减较小。因此,若不考虑反射波在底部边界的透射,即辐射阻尼,竖向地震能量需经坝基底部边界的多次反射才能被土体吸收,导致一致输入方法时竖向地震的加速度反应峰值的误差更大。在大坝稳定分析时,竖向地震反应是影响滑弧安全系数的重要参数,一致输入方法会大大低估大坝的抗滑安全性。近场地震的竖向峰值和水平向峰值接近[23-24],采用非线性波动输入方法研究覆盖层上土石坝遭遇近场区地震时的抗震安全十分必要。
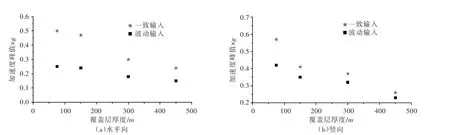
图9 不同覆盖层厚度时坝顶加速度反应峰值
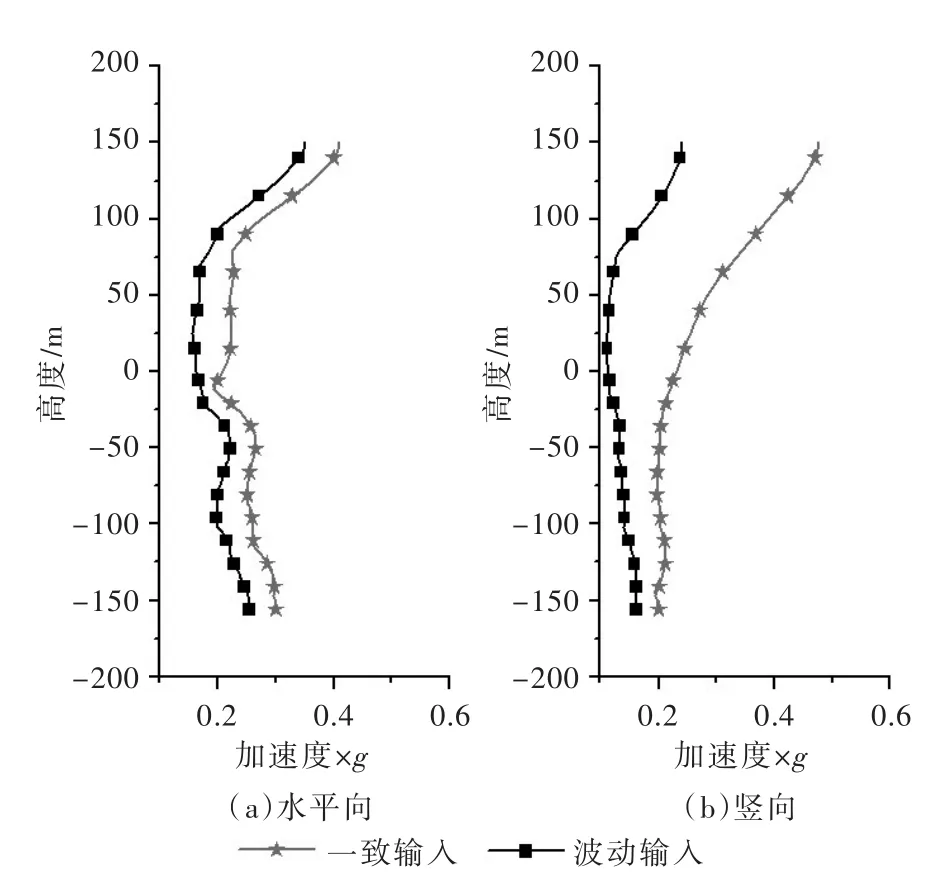
图10 大坝中部加速度峰值分布

图11 坝顶中部加速度傅立叶谱(归一化)
图9为坝顶加速度峰值随覆盖层厚度的变化。由图9可以看出,采用非线性波动输入方法的加速度峰值较一致输入方法的结果明显降低,且随着覆盖层的厚度增大,两种地震动输入方法结果的差别逐渐减小。这主要是因为随着覆盖层厚度的增大,覆盖层土体的材料阻尼对地震能量的吸收作用增强,造成自由场加速度幅值及由上部传递至底部边界处的地震能量减小。另一方面,当覆盖层厚度450 m时,波动输入方法的坝顶水平向和竖向加速度峰值相对一致输入的降低率仍达11.5%和37.5%。
图10为覆盖层厚度为150 m时大坝中部加速度峰值沿高程的分布(高程0 m以下为覆盖层)。由图10可以看出,两种地震动输入方法的水平向加速度峰值规律基本一致,在覆盖层加速度峰值有缩小的现象,在大坝有明显的放大作用。竖向加速峰值在覆盖层中呈现出的分布规律差别显著,一致输入方法表现放大效应而波动输入方法为缩小。采用一致输入方法时,穿过覆盖层的危险滑弧的安全系数会被低估。
图11为坝顶中部加速度时程的归一化傅立叶谱(即在傅立叶变换前将加速度时程的峰值放大或缩小至1 m/s2)。由图11可以看出,大坝水平向加速度反应的频谱含量在低频区(0.2~0.4 Hz)差别较为明显,而竖向加速度反应在高频区(1~2 Hz)差别较大。这是由于大坝水平向加速度反应主要受土体剪切模量影响,竖向加速度反应与土体压缩模量关系密切,而饱和土具有剪切模量较小而压缩模量较大的特性。采用一致输入方法时,在敏感频段内大坝的动力反应会被高估。
3.2 覆盖层土体动力特性 图12为覆盖层土体动剪切模量变化(对应工况5、2、6和7)时坝顶加速度峰值的变化情况。表4为不同剪切模量系数时坝顶加速度峰值降低率。
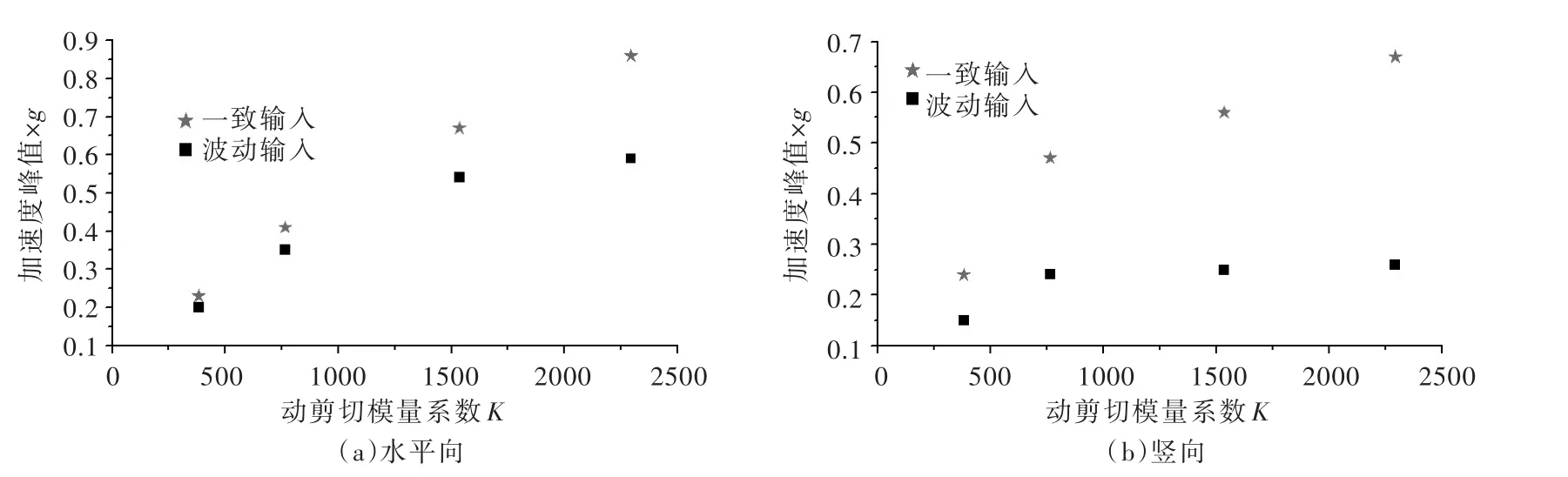
图12 不同覆盖层动剪切模量系数时坝顶加速度反应峰值

表4 不同剪切模量系数时坝顶加速度峰值降低率
由图12可以看出,随着覆盖层土体剪切模量的增大,一致输入方法获得的坝顶加速度反应峰值逐渐增大,而波动输入法的结果逐渐趋于稳定,且在竖向更为明显。因而,波动输入方法结果相对于一致输入方法结果的降低率逐渐增大,且竖向加速度的降低率明显大于水平向(见表4)。这主要由覆盖层土体的阻尼效应和饱和特性及波动输入方法的辐射阻尼效应造成的。
3.3 地震动强度 图13为地震动强度变化(对应工况8、9、2和10)时坝顶加速度峰值的变化规律。表5为不同地震动强度时坝顶加速度峰值降低率。
由图13可知,随着输入加速度峰值的增大,两种输入方法获得的坝顶加速度反应峰值均增大。同时由表5可知,波动输入方法相对于一致输入方法的降低率逐渐减小。这主要是因为随着地震动输入强度的增大,坝-基体系动力反应增强,土体动剪应变增大,阻尼提高,这会增强土体消耗地震能量的能力,辐射阻尼效应的作用相对减弱,一致输入方法的结果与波动输入方法差别减小。
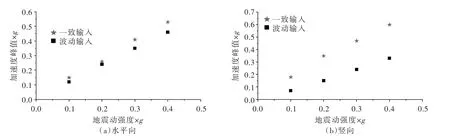
图13 不同地震动强度时坝顶加速度反应峰值

表5 不同地震动强度时坝顶加速度峰值降低率
3.4 地震波特性 图14为4种不同地震波时(对应工况2、11、12和13)两种地震动输入方法对应的坝顶加速度峰值。表6为不同地震波时坝顶加速度峰值的降低率。

图14 不同输入地震波时坝顶加速度反应峰值
由图14和表6可知,地震波类型对两种地震动输入方法结果的差异影响较大,并且对水平向和竖向加速度反应的影响程度不同。结合图7与图8中不同地震波的频谱特性,由表6可知,当地震波频率含量分布相似时(地震波1和地震波2),加速度反应谱谱值越高,一致输入方法的误差越大。对于地震波3,高频含量多且幅值高,而低频幅值较低,水平向加速度反应误差最小,但竖向加速度反应误差相对较大;对于地震波4,高频幅值较低,而低频幅值较大,水平向加速度反应误差较大,但竖向加速度反应误差相对较小。因此,对于覆盖层为饱和土的大坝,其水平向加速度反应对输入地震动的低频含量较为敏感,而竖向加速度反应对高频含量较为敏感。

表6 不同地震波时坝顶加速度峰值降低率
4 结论
本文为研究土石坝-覆盖层-基岩体系动力相互作用特性,分别采用传统一致地震动输入方法和非线性波动输入方法分析了覆盖层上土石坝的加速度反应,考虑了覆盖层厚度、土体动力特性、地震强度及地震波频谱特性的影响,对比并讨论了两种地震动输入方法的计算结果,阐明了采用非线性波动输入方法研究土石坝-覆盖层-基岩动力相互作用的必要性,得出如下结论:(1)通过统计并对比各工况下两种方法的计算结果可知:一致输入方法会高估覆盖层上土石坝的加速度反应。当采用理论上更为严密、能合理反映土石坝-覆盖层-基岩动力相互作用的非线性波动输入方法分析时,坝顶水平向和竖向加速度反应峰值均较一致输入方法降低,降低率分别为5%~32%和20%~62%。当输入地震动高频成分占主要时,一致输入方法获得的水平向加速度的误差较小,竖向加速度误差较大。(2)覆盖层土体的饱和特性使其压缩模量较大且受剪切模量影响较小。采用一致输入方法分析时,竖向地震波会在坝-基体系内多次往复传播以消耗其能量,这不仅造成大坝的竖向加速度峰值被明显高估(误差不小于20%),且其在覆盖层中的分布规律会由非线性波动输入方法获得的缩小效应变为放大效应。这不利于合理评价遭遇近场区地震(竖向分量突出)时覆盖层上土石坝的抗震安全。(3)对于覆盖层上的土石坝,水平向反应对地震动的低频含量较为敏感,竖向反应对地震动的高频含量较为敏感。采用非线性波动输入方法分析覆盖层上的土石坝时,较为准确地模拟了由大坝传播至截断边界处的地震波能量向无限远域的散射,加速度在敏感频段的放大效应明显减小。(4)加速度是开展覆盖层上土石坝抗震稳定分析的关键参数。采用一致输入方法分析时,大坝的极限抗震能力会被明显低估。因此,对覆盖层上土石坝进行抗震安全评价时,应采用能合理反映土石坝-覆盖层-基岩动力相互作用的地震动非线性波动输入方法。
