无资料或少资料区河流流量监测与定量反演
2018-12-07李甲振郭新蕾巩同梁
李甲振,郭新蕾,巩同梁,王 静,王 涛,李 慧
(1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038;2.西藏自治区水利厅,西藏 拉萨 850000;3.西藏自治区水文水资源勘测局,西藏 拉萨 850000;4.水利部水利水电规划设计总院,北京 100120)
1 研究背景
世界范围内80%的人口和65%的河流生态系统受困于不稳定的水资源供应,但人们对河流流量这一关键影响因素的了解甚少[1],只有不足60%的径流是在入海口进行了观测,内陆地区的监测点更为稀疏[2];受经济、政治因素影响,局部地区的水文测站数量自1980年代起就不断减少[3],一些水文站点也因缺乏维护管理而导致监测数据中断。对于无资料或少资料区,受限于恶劣的气候、不便的交通或复杂的地形条件,水文站点的建设、维护以及径流的监测就更加困难了。这些地区一般是在众多大江、大河源头和上游区域的西部地区,比如青藏高原-亚洲水塔,对整个流域水循环具有重要意义,因此,如何高效准确地对这些地区的河流流量进行监测成为水文研究需要解决的首要问题之一。
遥感以其高效、实时、观测范围广、数据量大等优点,在区域径流监测中发挥了重要的作用。基于遥感技术获取河道典型水力参数,反演河流流量,为上述问题提供了一种解决思路。国内外出现了地基高低频雷达遥感监测、航空摄影遥感监测、多光谱卫星遥感监测、全数字超高频雷达系统监测等手段,可对河道的长度和形状、水面宽、表面流速、水力坡度、地表植被等信息进行大数据量实时采集[4-5],推动了基于遥感的水文径流监测的发展;由美国、法国、加拿大以及英国等国家共同研制,并将于2021年发射的SWOT(Surface Water and Ocean Topography)卫星,其最重要的一个目标就是通过遥感获取所需数据,反演河流径流量[6]。根据流量反演所需水力特征参变量的个数,反演模型分为:单变量模型、双变量模型和三变量模型[4,7-9]。双变量和三变量模型中,引入了断面平均流速、断面平均水深和水力坡度这些参变量。断面平均流速需根据遥测的表面流速进行转换,其率定方法尚未成熟,且表面流速的观测受地面风向、风速等因素影响;另一方面,由于遥感技术对平面尺度的信息捕捉和分辨率优于垂直方向,因此,基于水位信息的单变量模型和多变量模型应用相对较少,基于水面宽反演河流流量的方法已成为该领域的研究热点。
Leopold和Maddock[8]通过对美国中西部和西南地区河流的水面宽和流量关系进行分析,首次建立了水面宽和流量之间关系的幂函数关系式。Park[10]研究了单站水力几何模型指数的变化规律,指数b的变化范围为0.00~0.59。在对单站水力几何模型研究的过程中,Gleason和Smith[11]发现了单站水力几何模型的系数与指数之间存在一定的函数关系,建立了多站水力几何模型,对密西西比河、亚大巴斯卡河、长江等河流典型河段进行流量反演的相对误差均值为20%~30%。之后,Gleason和Wang[12]给出了多站水力几何模型的数学理论依据。由于上述模型是基于水力学及地理信息学的统计学方法,源数据的处理以及误差的来源分析和控制也是研究的重点。Harman等[13]对澳大利亚东南地区河流进行了研究,水面宽、水深、流速和水力坡度的不确定度分别为4%、3%、7%和23%。Afshari等[14]提出了一种辨识现场调研数据随机误差和系统误差的递归过滤程序。针对河流整体连续信息获取较为困难这一情况,Pavelsky[15]利用空间不连续的卫星影像构建了塔纳纳河多个水面宽——流量关系曲线。国内相关研究大多是针对某一河流水力几何模型的系数和指数取值及其变化规律,例如,吴保生和李凌云[16]、马元旭和许炯心[17]以及冉立山等人[18]分别研究了黄河下游不同河段、无定河及其各支流以及黄河上游不同断面的水力几何模型的系数和指数取值及变化特征。赵春红和高建恩[19]给出了不同侵蚀沟(细沟、浅沟、切沟和冲沟)的水力几何模型的指数。
针对无资料或少资料区的径流监测难题,通过水力分析建立水面宽与流量函数关系的一般表达式,结合遥测遥感技术,提出一种水力学与遥感相耦合的径流反演方法,为无资料或少资料区的径流监测提供解决方案。
2 流量反演理论
河流流量计算公式为:

式中:Q为流量,m3/s;w为水面宽,m;d为断面平均水深,m;v为断面平均流速,m/s。
Leopold和Maddock[8]首次建立的水面宽、断面平均水深和平均流速与流量之间的函数关系式为:

式中:a、c和k为系数;b、f和m为指数。
将式(2)—式(4)代入式(1),a、c、k和b、 f、m满足如下关系式:

典型的河道过流断面如图1所示。图1(a)是常见于山区河流的一种过流断面形态。河道的纵比降大、水流流速快、冲刷力较强,水深、水面宽和过流面积随流量的波动变化大,具有V形河槽的特征。图1(b)是常见于山区和平原河流的一种断面形态,由于河道走势或地质的原因,其中一侧边坡陡,另一侧边坡缓,两侧边坡不同。对于平原区、丘陵区的河流,河道纵比降小,水流流速缓,过流断面的宽深比大,常见的断面形态如图1(c)和(d)所示。当河道中存在不能忽略的突起时,过流断面如图1(e)所示。
图1的(a)(b)可近似概化为三角形,其不同在于,图1(a)是左右对称的,是图1(b)的一种特殊情况。因此,本文将图1(a)(b)概化为图3所示的三角形断面进行分析。图1(c)(d)(e)所示的宽浅型河道,水面宽与水深的关系可近似概化为幂函数型,函数形式为 y=αxβ。假定过流断面的水面宽为100 m,水深为10 m,α和 β取表1给出的数值时,断面如图2所示。可以看出,根据幂函数y=αxβ与给定的α和 β值所绘制的断面形状,与实际工程中的一些宽浅型河道断面是相近的。因此,工程中的宽浅型断面是可以利用幂函数进行拟合的,只不过系数α和指数 β会随断面尺寸发生改变。

图1 河道过流断面的不同形态

表1 α和β取值

图2 河道概化断面示意图
2.1 三角形断面 典型的三角形断面如图3所示,其过水断面面积A的计算公式为:
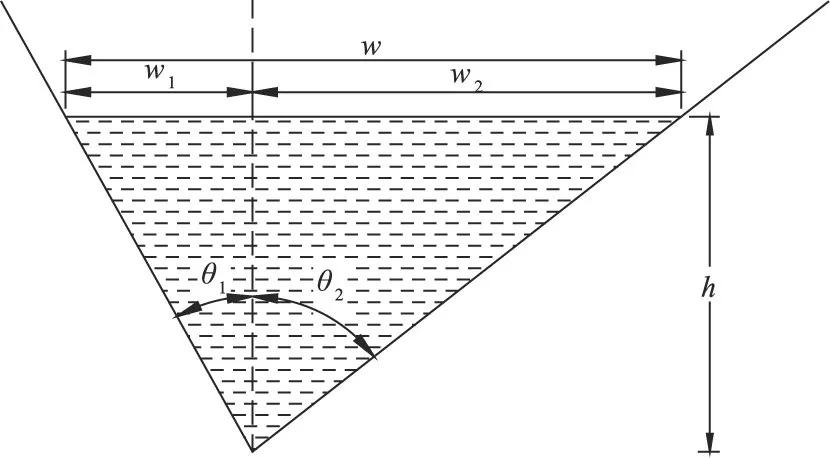
图3 三角形断面

式中:h为水深,m。
过水断面湿周 χ的计算公式为:
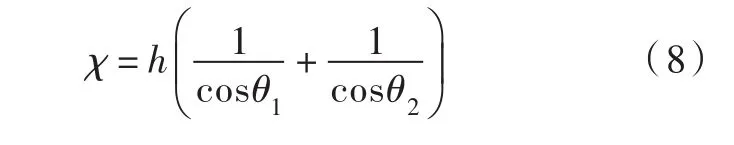
式中 θ1和 θ2为角度,°。
因此,水力半径R的计算公式为:

根据曼宁公式:

式中:J为水力坡度;n为曼宁糙率。
断面流速为:
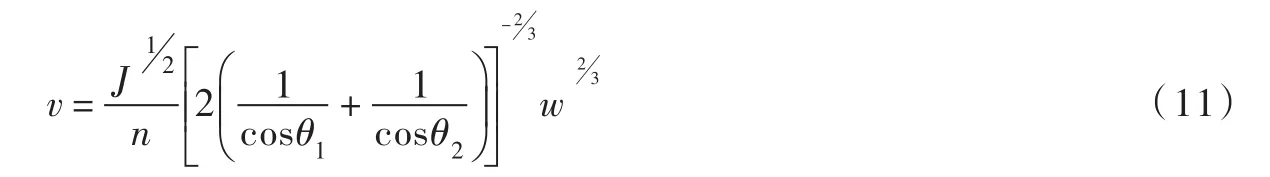
对于某一河道过流断面,水力坡度J、糙率n和顶角θ1、θ2均为常数,因此,流速v与正比例相关,即:

平均水深d的计算公式为:

因此,平均水深d与w正比例相关,即:

联立式(12)、式(14)和式(2)—式(4)可得:

式(15)和式(16)代入式(5)可得,三角形断面的指数分别为b=0.375,f=0.375,m=0.25。
2.2 幂函数型断面 典型的幂函数型断面如图4所示,断面方程为:
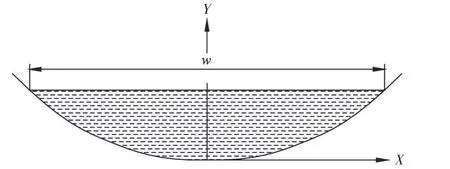
图4 幂函数型断面

过水断面面积A的计算公式为:

由于宽浅河道的湿周 χ近似等于河宽w[20],因此,水力半径的计算公式为:


断面平均水深d的计算公式为:

因此,断面平均水深d与wβ正比例相关,即:

联立式(20)、式(22)和式(2)—式(4)可得:

式(23)和式(24)代入式(5)可得幂函数型断面的3个指数分别为:

当 β=2时,河道断面为抛物线型,根据式(25)计算的3个指数b、 f和m分别为0.23、0.46和0.31 ,这与文献[21]给出的结果是一致的。当 β=1时,断面方程为 y=αx,也就是说,过流断面为三角形断面。由式(25)计算所得的3个指数b、 f和m分别为0.375、0.375和0.25,这与2.1的推导结果是一致的。
2.3 流量反演方法 由于现阶段遥测技术可较为准确捕捉的过流断面水力特征参数是水面宽,因此,本文构建的流量反演方法是基于遥测的水面宽。某一时刻的水面宽w0和流量Q0与t时刻的水面宽wt和流量Qt代入式(2),可得如下关系式

联立式(26)和式(27)得:

式(28)即为无资料或少资料区流量反演的理论基础。它反映了任一时刻的流量Qt与几个参数(水面宽wt、指数b、计算基数w0和Q0)之间的函数关系式,在确定指数b和计算基数w0、Q0后,即可直接依据遥测的水面宽进行流量反演。这就解决了传统设立水文测站进行测流所面临的站点建设和运营维护困难的问题,仅需进行一次测量就可以实现未来河流流量的远程实时监测。因此,本文提出了一种基于遥测、遥感与水力学模型相耦合的河流流量监测与定量反演方法。对于无资料区,也就是没有任何可参阅水文数据的地区,具体步骤为:
(1)选取河流断面,建设地面增强标识,作为遥感影像识别特征点。
(2)利用遥感或其他技术获得河流典型位置的断面特征,包括断面形态、水位H、水深D和水面宽w0,进而计算获得过水断面面积 A0、湿周 χ0和水力坡降J0。
(3)根据曼宁公式,计算当前水面宽w0对应的河道流量Q0:

式中n为糙率。糙率系数n根据工程界积累的不同边界材料及使用情况下的取值表格确定[22-23]。
(4)采用幂函数方程 y=αxβ对实测断面进行拟合,确定系数α和幂指数 β后,即建立了水面宽与水深、过流面积等参数间一一对应的函数关系;根据幂指数 β,由式(25)计算指数b。
(5)利用无人机或卫星得到的高精度遥感影像并结合地面增强标识点的尺寸辨识该断面任一时刻的水面宽wt。
(6)根据式(28)反演未来时刻的河道流量Qt。
针对少资料区,也就是以前有过水文测站或数据记录的地区,过流断面形状和计算基数可查阅相关资料获取,通过步骤(1)、(4)、(5)和(6)进行流量反演。
3 反演模型应用实例
利用模型实验和野外实测资料,对提出的无资料或少资料区河流流量监测与定量反演方法的应用进行展示和校验,分析反演方法的精度。
3.1 模型实验 模型实验在中国水利水电科学研究院水力学试验室展开,实验平台为自循环系统,主要包括变速泵供水系统、有机玻璃水槽和水位控制尾门等,如图5所示。变速泵供水系统由水泵和变频器组成,可调节水槽来流量;有机玻璃水槽长17.3 m、宽1.2 m、高0.25 m,其过流断面为复式断面;水位控制尾门采用推拉式结构,通过调节推拉门的开度控制下游水位。水槽来流量通过电磁流量计监测,水面宽采用卷尺进行测量。
利用幂函数形式对复式断面进行拟合,复式断面及其拟合断面如图6所示,函数关系式为y=1.65298x3.78366。由式(25)得,拟合断面的三个指数分别为b=0.13687、 f=0.51788和m=0.34525。
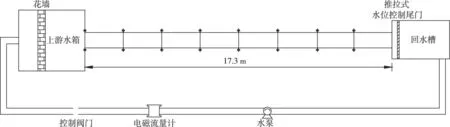
图5 模型实验平台
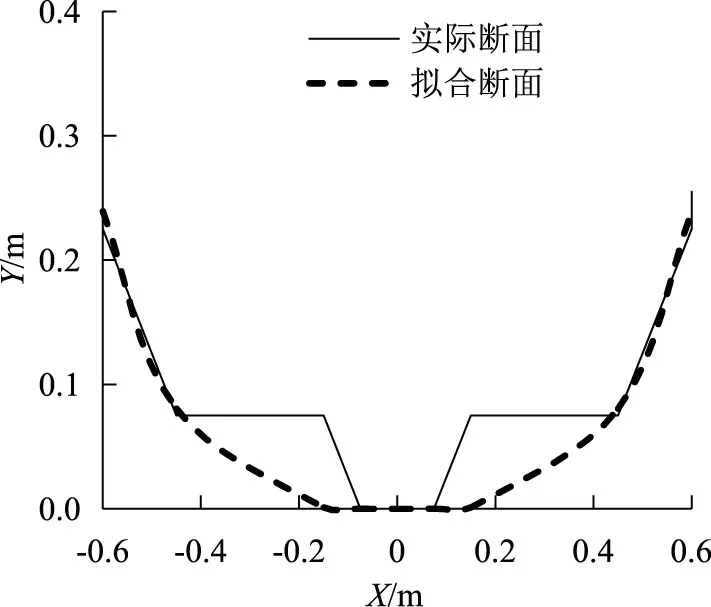
图6 实际断面与拟合断面
本文提出的方法是基于遥测的水面宽进行流量反演的,应用实例中,模型实验及野外实测均使用了测量的水面宽作为遥测数据。模型实验测试了9种不同工况的水面宽和流量,以工况5的水面宽w5和流量Q5作为计算基数w0和Q0,利用式(28)反演其他8种工况的流量,反演流量和实测流量如图7所示。其中,6种工况的反演流量与实测流量的相对误差小于20%。分别以工况1~9的水面宽和流量作为计算基数,对其他8种工况的流量进行反演,反演流量与实测流量的相对误差如图8所示。以工况1的实测水面宽w1和流量Q1作为计算基数w0和Q0,反演其他工况流量时,反演流量均小于实测流量,且相对误差大于20%;同样地,以工况9的实测水面宽w9和流量Q9作为计算基数
w0和Q0,反演其他工况流量时,反演流量均大于实测流量,且误差较大。分别以工况2~8的实测水面宽和流量作为计算基数反演其他工况流量时,相对误差均值为18.77%;56组反演流量中,40组与实测流量的相对误差小于20%,所占比重为71.43%。
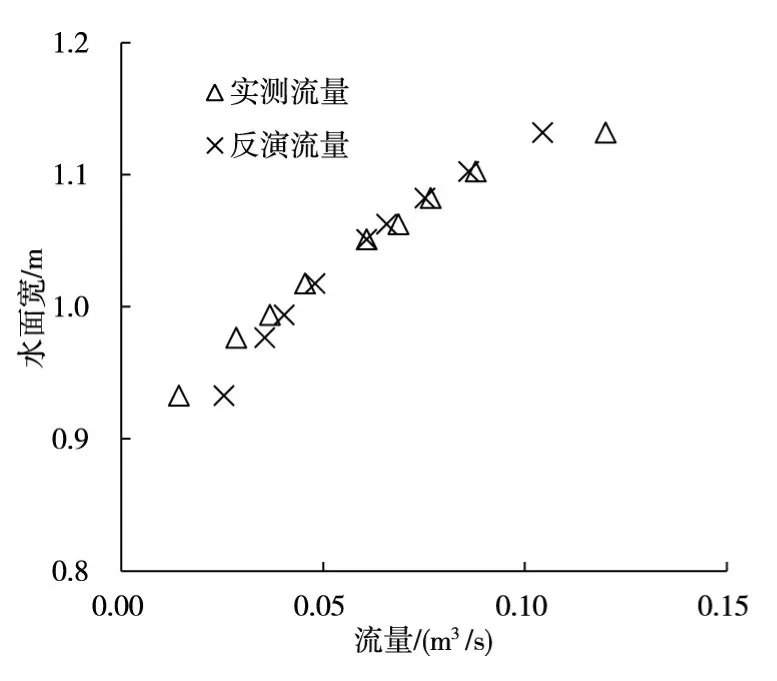
图7 实测流量与反演流量

图8 反演流量与实测流量的相对误差
3.2 野外实测 奴各沙站位于雅鲁藏布江上游河段,左岸为山体,右岸为河滩地,上下游500 m范围内水流平稳,断面均匀,河道水面与岸边对比度清晰。第二次青藏高原综合科学考察水利资源与工程科考分队于2017年11月在该站搭建了遥感水文增强野外标识设施,并对典型断面进行了现场测量。奴各沙站的过流断面与图1的断面(b)相近,可将其近似为三角形断面,过流断面及其拟合断面如图9所示。根据2.1的推导,三角形断面的水面宽与流量幂函数关系式的指数b为0.375。
实测的74组水面宽与流量数据如图10所示。以水面宽为基准,对上述实测的74组数据进行排序,水面宽最小的工况记为1,水面宽最大的工况记为74。分别以工况1、10、20、……、60和70的实测水面宽和流量作为计算基数,利用式(28)反演其他73种工况的流量,反演流量与实测流量如图11所示。以工况1和工况10的实测水面宽和流量作为计算基数进行流量反演时,反演流量小于实测流量;以工况70的实测水面宽和流量作为计算基数时,反演流量大于实测流量。以相对误差小于20%和30%为基准,计算使用不同计算基数的反演流量合格率,结果如图12所示。以工况20、30、40、50和60的数据为计算基数时,相对误差均值为20.71%;64.66%的反演流量与实测流量的相对误差小于20%,86.03%的反演流量与实测流量的相对误差小于30%。

图9 实测断面与拟合断面

图10 实测流量与水面宽

图11 反演流量与实测流量

图12 反演流量合格率
4 结论
针对现阶段由于复杂地形、恶劣气候或经济、政治等因素造成的无资料或少资料区所面临的河流流量监测难题,将常见的过流断面进行概化,通过水力分析构建了一种水力学与遥感相耦合的径流反演方法。
(1)对于三角形断面,水面宽、断面平均水深和断面平均流速与流量之间函数关系式的三个指数分别为0.375、0.375和0.25;对于方程为 y=αxβ的幂函数型断面,三个指数的取值分别为
(2)无资料区河流流量监测与定量反演方法包括:①建设地面增强标识点;②实测断面特征,包括断面形态、水位H、水深D和水面宽度w0,计算过流面积 A0、湿周 χ0、水力坡度J0;③根据河床及植被情况确定糙率系数n,计算过流量Q0;④采用幂函数方程 y=αxβ对实测断面进行拟合,确定系数α和幂指数 β,即建立了水面宽与水深、过流面积等参数一一对应的函数关系,根据幂指数 β计算指数b;⑤监测水面宽wt;⑥反演t时刻的流量Qt。对于少资料区,根据已有资料可确定断面形态和计算基数w0、Q0时,按照步骤①、④、⑤和⑥进行流量反演。
(3)根据模型实验水面宽反演的56组流量,相对误差平均值为18.77%;其中,40组反演流量与实测流量的相对误差小于20%,占比为71.43%。根据野外实测水面宽反演的流量,相对误差均值为20.71%;其中,64.66%的反演流量与实测流量的相对误差小于20%,86.03%的相对误差小于30%。
(4)提出的方法主要适用于河道过流断面可近似为三角形或幂函数型的情形,且具有一定的精度;在现阶段水文数据匮乏的无资料或少资料区,该方法可期成为一种有效的流量监测手段。当断面为其他形态或易冲淤时,可能会产生较大的误差,这也是进一步研究需要解决的问题。
