贝叶斯框架下的大坝变形交互式时变预测模型及其验证
2018-12-07李明超任秋兵
李明超,任秋兵,沈 扬
(水利工程仿真与安全国家重点实验室,天津大学,天津 300354)
1 研究背景
大坝是我国国民经济的重要基础设施,在防洪、发电和航运等方面发挥着巨大效益[1]。截至2016年,我国已建成水库大坝9.8万余座,是世界上水库大坝数量最多的国家[2]。水库大坝面临气候环境变化、运行条件复杂等多重风险,对大坝安全保障与风险管理提出了较高要求,推动大坝安全监控与性态预测研究成为当前坝工领域的热点课题。坝体变形是评价大坝结构性态转异和服役健康状况的重要指标[3-4],因而大坝变形分析及预测成为大坝工作性态预测的关键组成部分,其有效研究手段是依据实测变形资料,应用统计数学、信息科学等方法建立合理的数学监控模型并对大坝变形进行预报[5]。大坝变形预测模型的可靠程度直接决定工程师能否准确掌握坝体变形状态,并对超限形变及时采取相应措施,对于维护大坝安全运行和确保人民生命财产安全具有重要意义[6]。
大坝变形是一个包含多种随机性因素的复杂变化过程[7]。一方面,大坝在服役过程中受到环境(气温、降水等)、荷载(水压、自重等)及突发性灾害(洪水、地震等)等外部因素的共同作用,导致变形量不断发生改变[8];另一方面,位移、沉降等时变量也是大坝结构自身非线性、非稳态性等动态特征的集中体现[9]。总而言之,变形序列中各个实测值是内外多重影响因素在同一时刻发生作用的综合结果。为全面反映内外部因素对大坝变形过程的影响,采用时间序列分析(简称时序分析)方法深度挖掘变形数据序列(简称数列)的潜在规律[10],从而准确分析和预报大坝服役性态,是一种行之有效的方法。
时序分析是一种处理动态数据的参数化时域分析预测方法[11],该方法根据历史实测数据建立能够识别序列演变模式的数学模型,并进行外推来预测未知量[12]。时序分析早在1940年代便开始应用于工程领域[13],直至1970年代,《时间序列分析:预测和控制》[14]一书系统论述了自回归滑动平均模型(ARMA)成套理论及应用方法,时序分析实现跨越式发展。自此,国内外学者对时变模型展开深入研究,逐步丰富、完善时序分析理论结构,使其向非线性、非平稳以及随机场方向发展[15]。在水利工程领域,大坝变形预测方法借助时序分析理论取得显著进展,例如,吴中如等[16]运用时序分析、模糊数学等数理方法推导出一系列大坝安全监控模型,其研究成果在三峡、龙羊峡等重大水电工程中得到验证;汪树玉等[17]将时序分析和混沌理论相结合,提出利用Lyapunov指数和关联维数方法辨别数列混沌性,以建立全局和局部预测模型。
近年来,随着人工智能理论和计算机技术的不断发展,一些新的数学模型和计算方法相继出现,例如,苏怀智等[18]基于POT模型以超限测值样本序列代替年极值样本序列,并利用广义帕累托分布函数拟定大坝变形预警指标;吴斌平等[19]将灰色模糊模型和遗传神经网络模型作为子模型,采用考虑时间影响的神经网络模型作为组合模型权重的求解方法,并对某心墙堆石坝进行变形预测;Shao等[20]为解决传统回归方法中存在的多重共线性问题,提出一种新的基于面板数据理论的随机系数模型,并论述了不同测点间的潜在关系;Dai等[21]针对传统统计模型泛化能力较差的弊端,利用统计模型选取合适参数、提取解释变量,建立起适用于混凝土坝变形预报的优化随机森林回归模型;Su等[22]考虑到大坝变形的强非线性动态特征,遂将支持向量机与其他方法(如相空间重构、小波分析、粒子群优化算法等)相结合,构建出小波支持向量机变形预测模型。
然而,在应用现有变形预测模型进行大坝变形预报时,经常会遇到以下困难:(1)交互障碍:模型完全自主化,难以进行专业交互建模,造成大量有价值的专业信息被忽略;(2)寻参复杂:模型参数较多,难以直观理解,必须掌握模型底层方可准确调参;(3)优化不足:模型未根据变形监测数据特征进行优化处理。针对上述问题,本文提出一种耦合自动预测算法与专业知识的交互式变形预测模型(Interactive Deformation Prediction Model,IDPM),通过配置必要的直观参数实现交互式建模,同时简化参数寻优过程,并对原始数据噪声进行参数化清洗,借助可视化展示及评价指标反馈进行精准微调以提高模型适配性,从而有效地帮助工程师运用专业知识来达到准确预测大坝变形的目的。
2 总体框架
时间序列的构成要素有长期趋势成分T(t)、季节变动成分S(t)、循环变动成分C(t)和不规则变动成分I(t)。按照构成要素的组合方式不同,时变模型大致分成加法模型、乘法模型和混合模型三类[23]。考虑到大坝变形数列具有年周期性显著、季节波动相似等特征,且乘法模型可通过对数变换转化为加法模型,最终基于广义加法模型(GAMs)[24]建立 IDPM。现将分解项 S(t)、C(t)合并为 P(t),同时引入新成分M(t),得到改进后的加法模型:
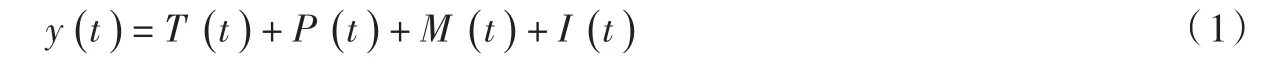
式中:T(t)为趋势项,是指变形数列长期呈现出的持续线性或非线性变动组分(见图1点划线标注);P(t)为周期项,是指变形数列中重复性的波浪形或振荡式变动组分(见图1实线标注);M(t)为标记项,是指受突发性灾害影响而造成变形数列的无规律剧烈变动组分;I(t)为随机误差项(简称误差项),表示变形数列中无法控制、不易度量的其他随机组分。

图1 某大坝测点PL17X方向变形监测数据(1988年1月—2014年12月)
IDPM主要包括自动预测模块和自定义配置模块两部分:(1)自动预测模块通过异常检测等算法实现自主预测大坝变形,仅需配置预测期等必要参数;(2)结合历史数据拟合程度等可视化信息以及均方误差(MSE)等量化指标反馈,工程师通过自定义配置T(t)、P(t)及M(t)三项中的直观参数来融入设计工况、科学预报等专业知识,进而完成高质量的大坝变形预测。上述两部分既能独立运行,又能协同合作,二者相辅相成,共同构建贝叶斯框架下的大坝变形循环预测体系,如图2所示。与季节性差分自回归滑动平均模型(SARIMA)[25]等传统时变预测模型相比,上述过程省略了平稳性检验、差分平稳化处理、复杂参数估计等步骤,使大坝变形预测变得简便高效。

图2 IDPM总体框架结构
直观参数化是实现交互式建模的关键,应用贝叶斯方法配置IDPM底层模型参数,既能降低模型结构复杂度,又能充分利用非样本信息[26]。其基本思路是:(1)假定待估模型参数为服从某种分布的随机变量,根据经验给出待估参数的先验分布(待估模型参数包括误差项I(t),根据中心极限定理假定I(t)服从正态分布;(2)将先验信息(非样本信息)与样本信息相结合,利用贝叶斯定理求出待估参数的后验分布;(3)构造损失函数,并以损失函数最小化为准则求得参数估计量。
3 IDPM原理
3.1 趋势项T(t)
3.1.1 线性趋势模型T1(t)大坝多数时间处于正常运行状态,其多年变形数列整体呈现持续性增加(或减小)的趋势,仅伴有小幅度的波动,如图1所示。在考虑预测模型拟合准确率的同时,还要兼顾其执行效率,因此优先选择简单、灵活的分段线性函数作为趋势模型。现以线性增长趋势模型为例,其基本表达式为:

式中:m为增长率,m>0;b为偏移量。
大坝变形增长率是不断变化的。例如,坝址区气温、降水等环境因素的时变性与不确定性,会对大坝变形增长率产生一定的影响。为适应实测变形数据的动态变化,模型必须能够囊括不同的增长率。当增长率发生改变时,通过定义转折点在模型中加入趋势变化。假设存在H个转折点依次对应于时间序列各点的趋势变化率定义为 μ∈RH,其中μi表示时间点xi的趋势变化率。为方便表述,定义示性函数那么时间点t>xi的趋势变化率为随着增长率m的改变,偏移量b需作相应调整,以确保整个分段函数的连续性以及平滑性。经推导可得,时间点xi处的偏移量调节率为ηi=-xiμi。综上,改进后的线性趋势模型为:

式中:m为基本增长率;μi表示趋势变化率;b为偏移量;ηi为偏移量调节率;为示性函数。

式中:Dmax为上限值;m为增长率,m>0;b为偏移量。
根据大坝变形增长规律,对式(4)作以下改进:其一,变形上限值并非常量,可用时变函数取代固定值Dmax;其二,与线性趋势模型类似,变形增长率m同为时变量,通过定义变化率 μ∈RH表示趋势拐点,引入偏移量调节率η∈RH保证分段函数的连续性,其中xi处的偏移量调节率ηi为:

因此,改进后的非线性趋势模型为:

3.2 周期项P(t)大坝变形数列的周期性主要是由气候季节性变化引起的。例如,我国大部分地区冬季寒冷干燥,夏季高温多雨[29],导致坝址区气温、降水等环境因素呈显著季节性变化,进而造成大坝变形的多年重复性年内变化,如图1所示。为描述大坝变形数列内的谐波关系,决定基于三角函数形式的傅里叶级数进行周期性建模。若给定一个循环周期为Q的周期函数P(t),满足Dirichlet条件,可以采用部分和(省略常数项)来近似表示其周期效应[30]:

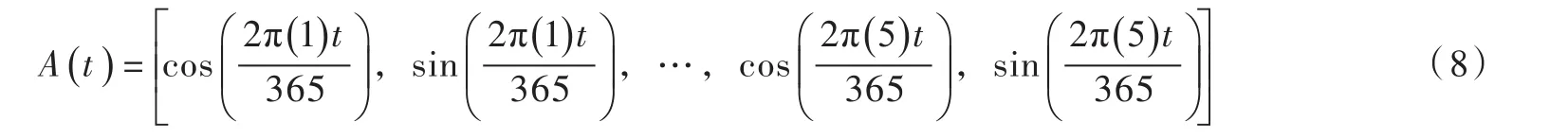
综上,变形数列中的周期性成分表示为:

式(9)中,假设傅里叶系数α存在先验分布N(0,σ2)以提高周期性模型的平滑性。当变形数列周期性变化较快时,可将低通滤波器(如巴特沃斯滤波器[31]等)应用于数列中,如此通过增加项数N即可拟合变化更快的周期效应。
3.3 标记项M(t)自然灾害对坝体变形的影响不可忽略。我国降雨量年内、年际变化较大,极易导致洪水等气象灾害的发生。除此之外,我国还是个多地震的国家[32]。而洪水、地震等自然灾害的发生多无固定模式可循,使变形预测问题变得更为复杂。传统时变预测模型(如SARIMA等)为了简化问题,通常将坝址区灾害引起的变形异常值作为噪声数据进行统一处理,难以实现精细化建模。
通过加入标记项M(t),IDPM可以表述突发性灾害对变形数列的影响。假设洪水、地震等自然灾害对变形数列的影响彼此独立,灾害d的发生时间定义为Id,引入指示函数表示时间点t是否处于灾害d发生期间,并为各灾害添加影响系数 β∈RK来描述灾害对变形数列的影响程度,其中βd表示因灾害d发生而引起的预测值变化。与周期性建模类似,通过构造矩阵B(t)来求解:

由此,标记项M(t)表示如下:

式(11)中,对影响系数β添加先验分布N(0,υ2)以防止过拟合。考虑到洪水、地震等自然灾害对变形数列的影响存在滞后性,故预置时间参数ΔWd来表征灾害持续影响期,并作如下假设:影响期ΔWd内变形数列也会受到灾害d的影响,且与灾害d发生期间所受的影响等价。以此为基础,通过调整ΔWd即可完成灾害滞后性影响的数学建模。

图3 某大坝测点PL17Y方向变形监测数据(1988年1月—2014年12月)
4 IDPM构建与实现
4.1 前端处理 由监测仪器故障引起的突变值、离群值(如图3所示)往往会扭曲预测结果并影响模型精度。为此,IDPM通过对模型参数添加稀疏先验进行正则化处理[33],不仅实现自动识别输入扰动,更进一步实现参数化配置检测。假设实测变形数列中存在若干突变值,采用3.1节所述方式定义突变值 xa∈X ,通过对式(3)、式(6)中的趋势变化率μ添加先验分布μa~Laplace(0,ρ)以实现L1正则化,其中ρ为控制变化率μ集中情况的超参数,那么调节尺度参数ρ即可控制模型受突变值影响的程度,从而避免过拟合。尤其值得一提的是,加在μ上的拉普拉斯先验并不会对基本增长率m造成影响。对于离群值的处理,同样采用上述方式,兹不赘述。
4.2 参数配置 预测模型的优劣基本由预测效果来评判,而预测效果又往往依赖于参数配置。减少模型参数数量、降低参数配置难度,不仅能简化参数寻优过程,更重要的是毋庸掌握模型底层原理即可进行预测。通过对多测点变形预测结果进行综合评价,选取最佳参数组合作为模型参数缺省值,以实现IDPM自动变形预测。此时,仅需根据输入数列变化特征选择线性模型T1(t)或非线性模型T2(t),并指定预测期Δt即可完成变形预测任务。需要注意的是,时变上限值Dmax(t)作为非线性趋势模型T2(t)的主要参数之一,会对大坝变形预测效果产生重要影响。工程师可以根据大坝实际运行情况设置对应设计工况下的上限值Dmax(t),也可凭借工程经验或查阅历史实测上限值资料预估Dmax(t)。因此,进一步提高IDPM的可信度和准确率必须依靠人工参与建模才能够实现。
模型预测效果主要取决于对样本数据的拟合程度,其中以样本频率与特征值点(主要包括由气候季节性变化引起的趋势转折点、因地震等突发性灾害造成的异常值以及监测仪器故障等导致的突变值、离群值)对拟合优度的影响最大。为了提高模型拟合优度,一方面,需选取合适的趋势模型T(t),并设定与实测变形数列相匹配的预测频率f(如日、月等)。另一方面,考虑到仅凭检测算法难以准确判断特征值点位置,故需手动配置以下参数:(1)在趋势项T(t)、周期项P(t)中,通过指定时间拐点xi、调整傅里叶展开式项数N,以及改变先验分布参数σ来控制季节性变化,进而准确拟合趋势转折点。(2)标记项M(t)允许工程师在实测变形数列中划定出因历史洪水、地震等引起的异常值,并将其影响延续到预测期。工程师也可借助灾害持续影响期ΔWd、先验分布参数υ等来拟合异常值。(3)至于突变值、离群值等噪声的去除,可以在前端处理阶段通过设置监测错误数量ne、确定监测错误日期de,以及调节尺度参数ρ来完成。(4)如果不满足于利用上述方式来间接影响预测结果,可以根据地震预报、经验假定等辅助信息,在M(t)中指定预测日期来直接干预未来变形量。此外,通过借鉴SARIMA模型决策标准,部分模型参数可依照贝叶斯信息准则(BIC)[34]进行自动抉择。
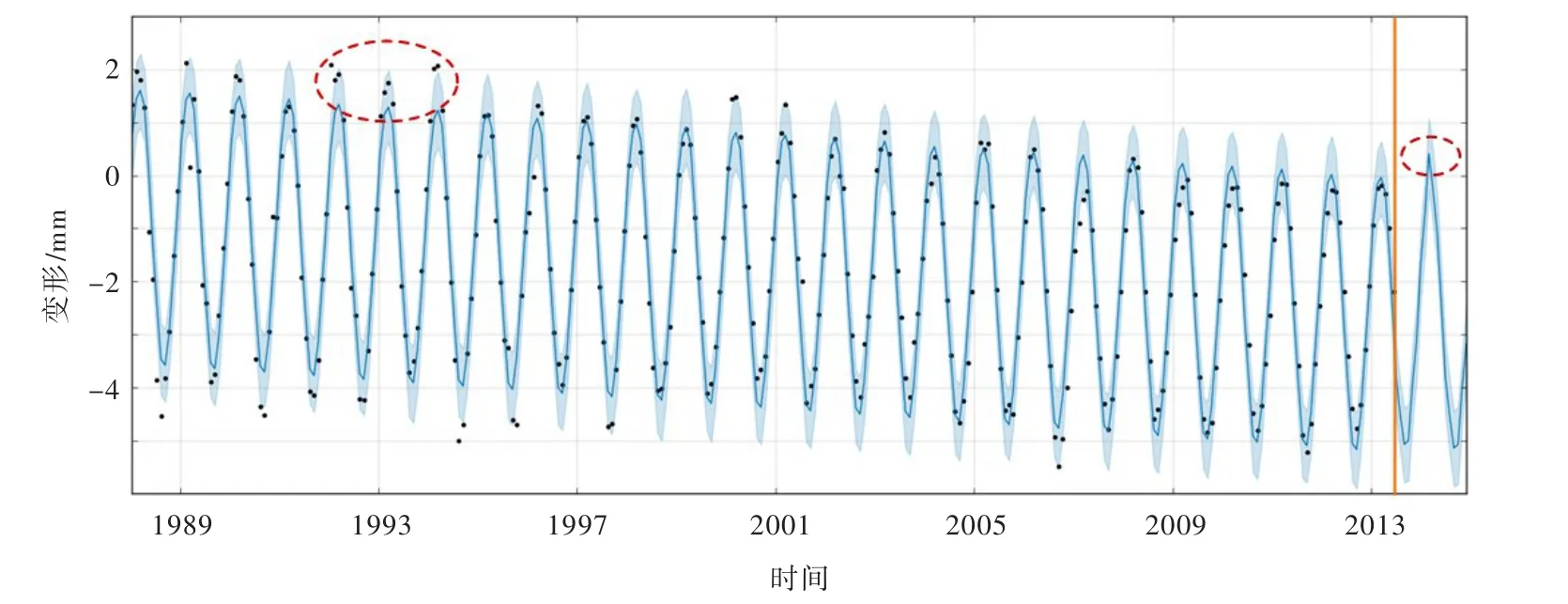
图4 某大坝测点PL17X方向变形监测数据拟合及预测可视化(1988年1月—2014年12月)
4.3 反馈优化
4.3.1 可视分析 拟合可视化能直观表现模型对样本数据的整体拟合优度。假设抽样频率fs固定不变,根据贝叶斯定理引入多层先验分布进行参数估计,以确定某一置信水平(文中置信水平统一取为0.9)下样本数据的拟合估计区间,并将其转换成图像。图4所示竖线左侧为实测期,其中圆点表示变形监测数据,着色区域表示估计区间端点包络带,各区间中点依次连接形成折线。通过观察实测数据与折线的偏离情况及其在包络带中的分布状态,工程师可大致评判模型拟合程度,并迅速对特征值点加以修正。IDPM根据修正指令实时显示对应参数组合下的预测值及其估计区间(见图4竖线右侧区域),方便后续针对性精准调参。以图4所示为例,缺省配置下模型总体拟合程度较好,但部分趋势拐点数值较大,致使模型过拟合,进而导致预测峰值过大,此时通过指定相应转折点或调整先验分布参数σ即可完成模型修正。因此,拟合优度、预测结果并行可视化大大提高了交互式建模的效率。
4.3.2 指标评估 为构建综合评价体系,兼顾定性分析与定量分析,现引入以下3项统计指标对模型进行补充评估。
(1)均方误差(MSE)是指实测值与预测值之差平方的期望值,其公式如下[35]:

(2)平均绝对误差(MAE)是指实测值与预测值之差绝对值的期望值,其公式如下[36]:

(3)平均绝对百分误差(MAPE)采用百分比对模型的无偏性进行评价,其公式如下[37]:

5 工程实例验证
基于上述模型方法,以某大坝多测点变形监测数据为例,对IDPM进行准确性、鲁棒性以及灵活性验证,旨在通过此实例说明IDPM在大坝变形预测方面的优势。某水利枢纽工程主要由挡水大坝、电站厂房、冲沙闸、泄水闸及船闸构成,其控制流域面积为100万km2,总装机容量达271.5万kW,具有发电、防洪、航运、灌溉等综合效益。其中,挡水大坝坝顶全长2 606.5 m,最大坝高47 m,主坝坝型为混凝土闸坝。现采用该坝右岸厂房坝段的垂线测点PL17X、PL17Y、IP17X以及IP25X方向变形监测数据(X方向表示与坝轴线垂直的方向,Y方向表示与坝轴线平行的方向),变形监测时段为1988年1月至2014年12月,每月进行一次数据采集,共计4×324个实测变形数据。利用三次Hermite插值方法[38]对PL17X、IP17X以及IP25 X方向变形监测原始数据进行均匀化处理,插值结果分别见图1、图5和图6,对PL17Y方向数据则不作任何处理(见图3),从而为后续仿真实验奠定数据基础。此外,鉴于IDPM需要结合专业知识进行精确建模,因此工程师对大坝整体情况的了解程度会直接影响变形预测结果。

图5 某大坝测点IP17X方向模型灵活性验证结果(1988年1月—2014年12月)

图6 某大坝测点IP25X方向模型灵活性验证结果:变形监测数据(1988年1月—2014年12月)
5.1 准确性验证
5.1.1 不同预测期 为验证不同预测时长下的模型准确性,选用正垂测点PL17X方向变形监测数据,确定实测时长为300个月(1988年1月—2012年12月),拟定预测时长分别为6个月(2013年1月—2013年6月)、12个月(2013年1月—2013年12月)、24个月(2013年1月—2014年12月)。图7为不同预测时长实测值与预测值的对比结果。由图7可见,模型预测趋势变化与实测数列基本相同,且预测值估计区间包络带覆盖所有实测数据点。通过对表1中量化指标进行分析,不同预测时长的变形预报精度大体一致,其中12个月和24个月的预报精度并未随着预测期的增加而骤然降低,说明IDPM可用于大坝变形长期预测。

图7 模型准确性验证结果(相同实测期、不同预测期)

表1 模型准确性验证
5.1.2 不同实测期 以正垂测点PL17X方向变形监测数据为例,将预测期定为12个月(2014年1月—2014年12月),通过拟定3组实测期,分别为36个月(2011年1月—2013年12月)、144个月(2002年1月—2013年12月)、312个月(1988年1月—2013年12月),来比较不同实测时长下的变形预测效果见图8。由图8可见,当实测时长较短时,IDPM未能准确识别出实测数列潜在规律,导致趋势预测出现较大偏差;反之,当实测期较长时,模型整体预测效果较好。这在表1中也有体现,各项统计指标随着预测时长的增加而逐渐减小。显然,IDPM在历史观测资料充足情况下的变形预测效果较好。

图8 模型准确性验证结果(相同预测期、不同实测期)
5.2 鲁棒性验证
5.2.1 随机插入离群值 选择正垂测点PL17X方向变形监测数据作为研究对象,实测期定为312个月(1988年1月—2013年12月)、预测期定为12个月(2014年1月—2014年12月),通过改变原始变形数列中干扰项的数量,来检验IDPM对噪声数据的抗干扰能力。应用随机函数向实测样本中插入不同数量的离群值,所得预测结果如图9所示。由图9可知,随机插入离群值数量越少,模型预测值估计区间包络带形状越显狭长。表2中引入原始变形数列所得预测结果进行比较,随着插入离群值数量的增加,相应预测精度逐渐下降,但总体预测效果较好,并未出现过大偏差。因此,IDPM对噪声干扰有一定的鲁棒性。
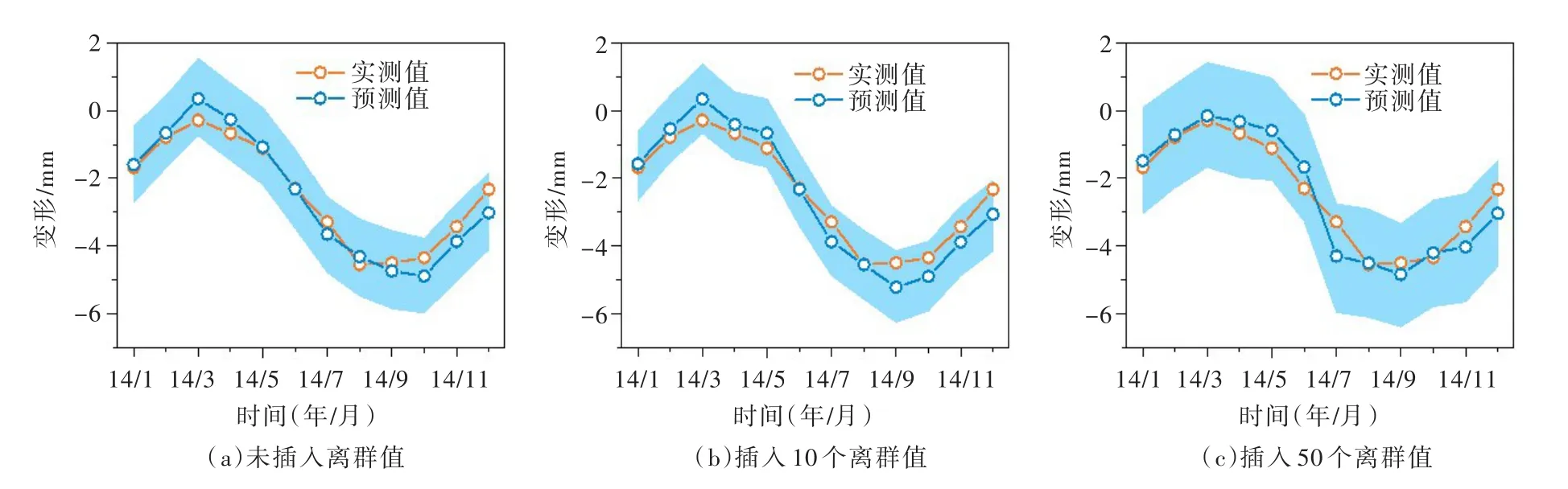
图9 模型鲁棒性验证结果(随机插入不同数量离群值)

表2 模型鲁棒性和灵活性验证
5.2.2 非定期变形监测 考虑到大坝正常运行阶段通常采用非定期变形监测方法,即观测时间间隔不固定,故以正垂测点PL17Y方向变形监测原始数据为例,检验IDPM针对此工况的优化效果。现确定实测期为300个月(1988年1月—2012年12月),拟定预测期分别为6个月(2013年1月—2013年6月)、12个月(2013年1月—2013年12月)、24个月(2013年1月—2014年12月)。通过对预测结果与实测数列的对比(如图10所示),模型预测趋势拐点与实测数列基本吻合,仅有局部少数实测点未被预测值估计区间包络带所覆盖。从表2中也可见不同预测时长的变形预报精度相仿。这说明IDPM可用于非定期监测工况下的大坝变形预报。

图10 模型鲁棒性验证结果(非定期变形监测)
5.3 灵活性验证 人工参与建模扩大了IDPM的适用范围。应用IDPM对该坝多测点进行变形预报,均表现出稳定且良好的预测效果。因篇幅所限,本文仅选取两倒垂测点IP17X、IP25X方向长期变形监测数据作为示例,其中测点IP17X方向变形序列中间阶段出现大范围波动,局部趋势不明显(见图5竖线左侧区域),测点IP25X方向变形序列靠后阶段趋势出现拐点向下,发生走向突变(见图6竖线左侧区域)。要而言之,两测点相应方向实测数列变化频率较快、幅度较大,序列演变规律不易被识别。现统一拟定实测时长为300个月(1988年1月—2012年12月)、预测时长为24个月(2013年1月—2014年12月),来验证模型对测点IP17X、IP25X方向变形数列的适应能力。通过对两测点预测结果和对应实测值的比较(分别见图5、图6竖线右侧区域),模型预测趋势与实际情况大体相同,除部分转折点外,其余实测点均被预测值估计区间包络带所覆盖。由表2也可得,各测点对应精度指标基本满足大坝变形预报要求。综上所述,IDPM具有较好的灵活性。
6 结论
本文提出一种新的大坝变形交互式时变预测模型,其借助参数化、可视化融合坝工领域知识,可有效完成大坝变形预测优化循环过程。基于所提出的模型,以某混凝土坝多测点长期变形监测数据为例,通过控制预测时长、离群值数目等关键变量进行多组仿真实验,结果表明该模型在变形预报方面优势明显,主要表现为:(1)通过全过程配置直观参数,打破了自动预测算法与科学预报等专业知识之间的壁垒,实现了交互式数学建模;(2)在历史观测资料充足的情况下可用于大坝变形长期预测,克服了传统时变预测模型多适用于短期变形预测的弊端;(3)对于突变值、离群值较多和非定期变形监测等产生的噪声干扰具有一定的鲁棒性;(4)输入不同变形数列,其参数无需全部重新设定,具有较强的适应能力。鉴于交互式变形预测模型能够发挥大坝变形实测数列和坝工领域知识的组合作用,更适合应用于变形监测数据完整性较好、可靠性较差情况下的大坝变形快速、精确预报。目前该模型主要研究了变形序列自身规律,未充分考虑环境、荷载等外部因素对大坝变形的直接影响,故将上述因素纳入到模型中是下一步研究的重点。
