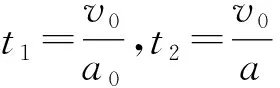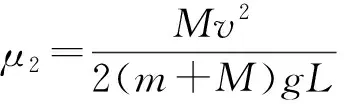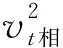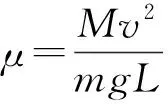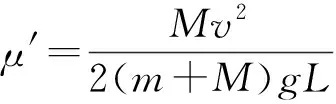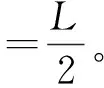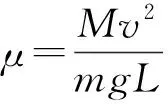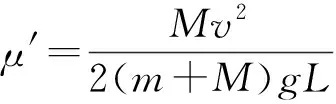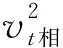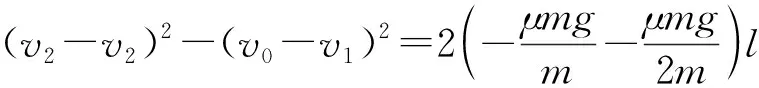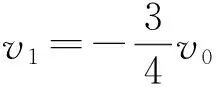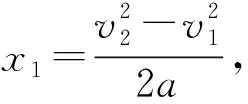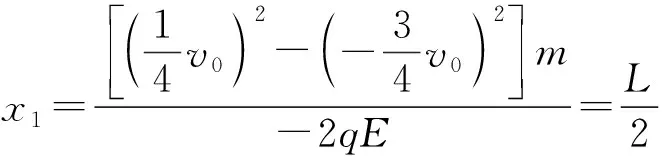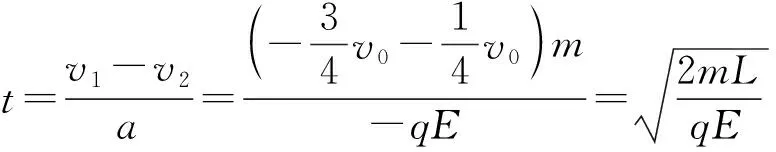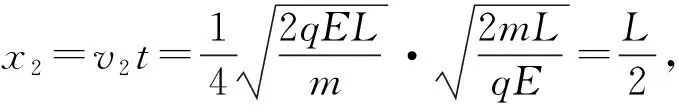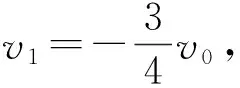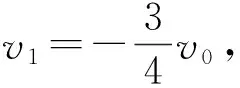求解相对位移的三种方法比较

2018-12-07重庆杨天才

教学考试(高考物理) 2018年5期

重庆杨天才

两个物体之间的相对运动是一种常见的运动形式，即某一物体对另一物体而言的相对位置的连续变动，如：追及问题、传送带问题、滑块木板问题、碰撞问题等。笔者将引入相对位移公式来探究其中的典型模型，同时图象和数学公式虽然都能反映物体的运动规律，但图象比公式直观、简便、巧妙，有独特的优越性，特别是在分析解决两个物体之间的相对运动时尤为突出。以下是三种方法的比较：

【例1】甲火车正以速率v1向前行驶，司机突然发现正前方同一轨道上距离为x处有另一火车乙，正以较小的速率v2沿同方向做匀速运动，甲车司机由发现情况到开始刹车所用时间(反应时间)为Δt，甲车在刹车过程中做匀减速运动。要使两列火车不相撞，甲车刹车时的加速度a的大小至少应是多少？

【原解】两车恰好不相撞时，二者速度相同，均为v2，设甲车由刹车到共速所用时间为t，加速度大小为a

x甲=x+x乙

x甲=v1Δt+v1t-at2/2

x乙=v2(Δt+t)

v2=v1-at

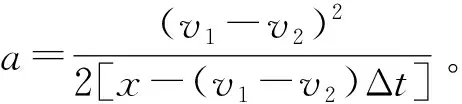
【相对位移法解析】反应时间内两车匀速运动

由x相=v相t，甲相对乙的位移为x1=(v1-v2)Δt

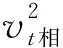
甲车相对乙车的运动满足

(v2-v2)2-(v1-v2)2=2(-a-0)(x-x1)

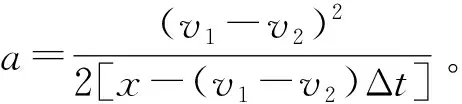
【图象法解析】设甲车由刹车到共速所用时间为t，加速度大小为a，在同一坐标系内画出甲、乙火车运动的v-t图象，如图1所示,由题意阴影部分面积在数值上等于相对位移，即

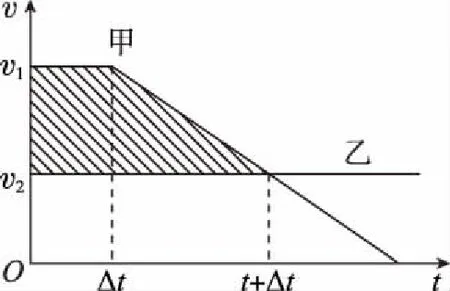
图1

【例2】一水平的浅色长传送带上放置一煤块(可视为质点)，煤块与传送带之间的动摩擦因数为μ。初始时，传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动，当其速度达到v0后，便以此速度做匀速运动。经过一段时间，煤块在传送带上留下了一段黑色痕迹后，煤块相对于传送带不再滑动，求此黑色痕迹的长度。

【原解】根据“传送带上有黑色痕迹”可知，煤块与传送带之间发生了相对滑动，煤块的加速度a小于传送带的加速度a0。根据牛顿运动定律，可得a=μg

设经历时间t，传送带由静止开始加速到速度等于v0，煤块则由静止加速到v，有

v0=a0t

v=at

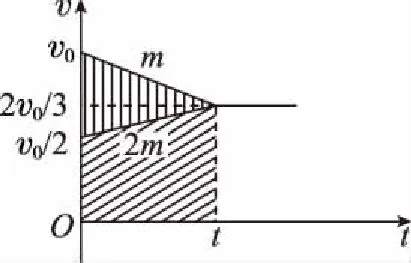
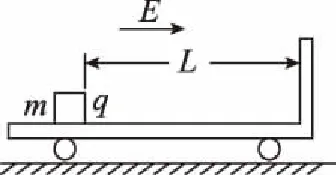
由于a

再经过时间t′，煤块的速度由v增加到v0，有

v0=v+at′

此后，煤块与传送带运动速度相同，相对于传送带不再滑动，不再产生新的痕迹。

设在煤块的速度从0增加到v0的整个过程中，传送带和煤块移动的距离分别为x0和x，有

传送带上留下的黑色痕迹的长度l=x0-x

【相对位移法解析】同理a=μg，设经历时间t1，传送带由静止开始加速到速度等于v0

设经历时间t2，煤块由静止开始加速到速度等于v0

黑色痕迹的长度为

图2

【图象法解析】同理a=μg

设经历时间t1，传送带由静止开始加速到速度等于v0

设经历时间t2，煤块由静止开始加速到速度等于v0

在同一坐标系内画出传送带和煤块运动的v-t图象，如图2所示

【例3】如图3所示，一块质量为M，长为L的均质板放在很长的光滑水平桌面上，板的左端有一质量为m的小物体(可视为质点)，物体上连接一根很长的细绳，细绳跨过位于桌边的光滑定滑轮。某人以恒定的速率v向下拉绳，物体最多只能到达板的中点，而板的右端尚未到达桌边定滑轮处。试求：

(1)物体刚到达板中点时板的位移；

(2)若板与桌面之间有摩擦，为使物体能达到板的右端，板与桌面之间的动摩擦因数的范围是多少。

图3

【原解】(1)m与M相对运动时，m匀速运动有vt=x1

M匀加速运动有vt/2=x2x1-x2=L/2

联立以上三式得x2=L/2。

(2)设m与M之间摩擦因数为μ1，当桌面光滑时有

μ1mg=Ma1v2=2a1x2

如果板与桌面有摩擦，因为M与桌面摩擦因数越大，m越易从右端滑下，所以当m滑到M右端两者刚好共速时摩擦因数最小，设为μ2

【相对位移法解析】(1)设板的加速度、位移分别为a、x板，则由题意有v2-02=2ax板

(2)设小物体和板间的动摩擦因数为μ

v2=2ax板

设板和地面间的动摩擦因数为μ′，同理，物体相对板满足

(2)若小物体和板间的动摩擦因数为μ，

设板和地面间的动摩擦因数为μ′

同理板的位移与物体比板多运动的位移相等，即

x板=L

【例4】如图5，在一光滑的水平面上有两块相同的木板B和C。重物A(视为质点)位于B的右端，A、B、C的质量相等。现A和B以同一速度滑向静止的C、B与C发生正碰。碰后B和C粘在一起运动，A在C上滑行，A与C有摩擦力。已知A滑到C的右端而未掉下。问：从B、C发生正碰到A刚移到C右端期间，C所走过的距离是C板长度的多少倍。

图5

【原解】设A、B、C的质量均为m。碰撞前，A与B的共同速度为v0，碰撞后B与C的共同速度为v1。对B、C，由动量守恒定律得mv0=2mv1

设A滑至C的右端时，三者的共同速度为v2

对A、B、C，由动量守恒定律得2mv0=3mv2

设A与C的动摩擦因数为μ，从发生碰撞到A移至C的右端时C所走过的距离为x，对B、C由功能关系

设C的长度为l，对A由功能关系

在同一坐标系内画出A和BC运动的v-t图象如图6所示

图6

C所走过的距离与C板长度的比值为

【例5】一个质量为M的绝缘小车，静止在光滑水平面上，在小车的光滑板面上放一质量为m、带电荷量为+q的带电小物块(可视为质点)，小车质量与物块质量之比M∶m=7∶1，物块距小车右端挡板距离为L，小车车长为 1.5L，如图7所示，现沿平行车身方向加一电场强度为E的水平向右的匀强电场，带电小物块由静止开始向右运动，而后与小车右端挡板相碰，若碰后小车速度大小为碰撞前小物块速度大小的1/4，并设小物块滑动过程及其与小车相碰的过程中，小物块带电荷量不变，且碰撞时间极短、总能量不变。