基于分数阶阻抗模型的磷酸铁锂电池荷电状态估计

2018-12-06孙国强任佳琦成乐祥卫志农臧海祥

电力系统自动化 2018年23期

孙国强, 任佳琦，成乐祥，朱瑛，卫志农，臧海祥

(1. 河海大学能源与电气学院，江苏省南京市 210098； 2. 国网南京供电公司, 江苏省南京市 210019)

0 引言

为改善生态环境和应对化石能源利用危机，以电能为核心和可再生能源开发利用为基础的能源变革正蓬勃兴起。电储能系统作为关键装备，具有响应迅速、安装便捷的特点，在电动汽车、抑制新能源发电出力波动和电网辅助服务等方面发挥了重要作用[1-6]。其中，锂离子电池(以下简称锂电池)因其能量密度高、安全可靠等特点已被广泛应用。2017年，全球新增投运的电化学储能项目装机规模达914 MW，其中锂离子电池占比超过90%。截至2017年底，中国电化学储能累计装机规模达389.8 MW，锂离子电池的累计装机规模占比最大为51%，且增长迅速。

荷电状态(SOC)估计是储能系统安全高效运行的重要保障。文献[7]依据锂电池内部带电粒子的传质过程和离子浓度的扩散过程并考虑电化学反应中的热行为建立模型，估计精度较高。但模型由多个偏微分方程组成，计算复杂。文献[8-9]计及锂电池充放电过程中的迟滞特性，建立二阶RC网络模型，并采用扩展卡尔曼滤波有效减小锂电池SOC估计误差。但该方法将状态转移矩阵泰勒展开并忽略高阶项，可能导致截断误差。文献[10-11]根据锂电池电化学阻抗谱建立简化分数阶阻抗模型，同时为了降低参数辨识复杂度，将描述锂电池浓差极化的Warburg阻抗简化为0.5阶，这也在一定程度上限制了模型的准确性。针对锂电池的强非线性工作特点，文献[12-14]利用无迹变换(unscented transformation,UT)近似计算状态预测的后验均值和协方差，保证滤波精度为二阶甚至更高。为了进一步减小不确定性噪声的影响，文献[15-16]分别提出利用模型输出残差更新噪声协方差和平方根采样以提高估计算法的适应性，但上述方法中锂电池模型的精度不高，存在估计发散的可能性。

针对锂电池内部电化学反应的不确定性和复杂性，本文建立了一种锂电池的分数阶阻抗模型，该模型利用分数阶元件准确描述锂电池固液界面(solid electrolyte interphase,SEI)输运现象和极化反应，其物理意义更为明确。同时针对该锂电池分数阶阻抗模型强非线性的特点，基于分数阶阻抗模型的分数阶无迹卡尔曼滤波(fractional-order unscented Kalman filter,FUKF)算法估计锂电池SOC，实验结果表明，锂电池分数阶阻抗模型可准确描述锂电池工作特性，FUKF算法在SOC估计精度和跟踪速度上较无迹卡尔曼滤波(unscented Kalman filter,UKF)和分数阶卡尔曼滤波(fractional-order Kalman filter,FKF)有一定的提升，具备工程应用价值。

1 锂电池分数阶阻抗模型

电化学阻抗谱技术是对锂电池施加不同频率的小幅值正弦波电流信号测其交流阻抗，在不同SOC状态下其形状基本一致。图1描述了锂电池不同等效电路模型的阻抗特性曲线，由电化学阻抗谱理论可知，整数阶等效电路模型中RC网络在阻抗谱中为一个半圆，难以完整和准确地描述锂电池电化学阻抗曲线。因此，有必要引入分数阶元件分段拟合电化学阻抗曲线，以建立精确的电池模型[17-19]。锂电池电化学阻抗如图1所示。

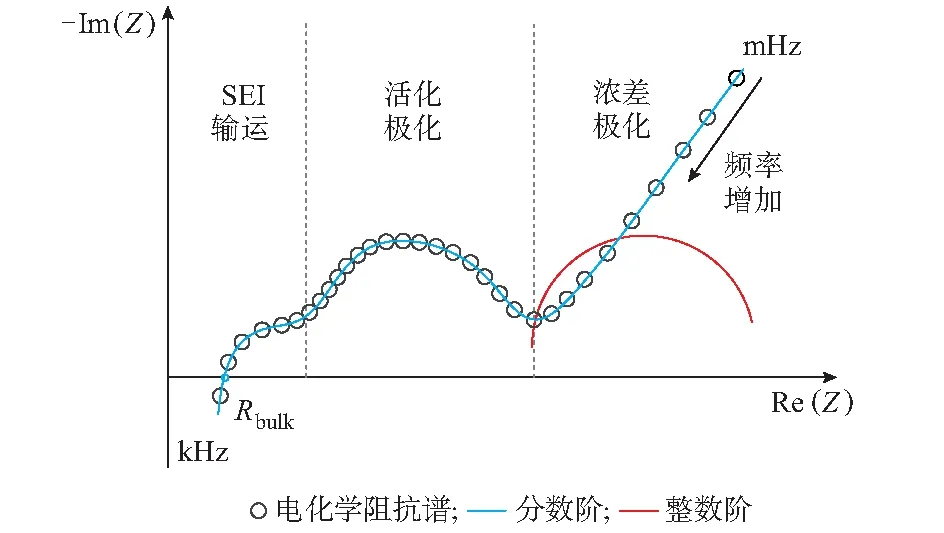
图1 锂电池等效电路模型阻抗特性对比Fig.1 Comparison of impedance characteristics for lithium-ion battery equivalent circuit models

由图1可知，阻抗特性曲线可分为高频、中频、低频3个部分。阻抗曲线高频部分与实轴相交处表征锂电池体相阻抗(bulk resistance)，由Rbulk表示；阻抗曲线高频部分为扁平半圆曲线的一部分，表征锂电池内部离子在SEI的输运现象，由常相位元件CPE1和电阻R1并联表示；阻抗曲线中频部分为扁平半圆曲线的一部分，表征锂电池内部的电荷转移过程(活化极化)，由常相位元件CPE2和电阻R2表示；阻抗曲线低频部分为直线段，表征锂电池电化学反应离子的扩散现象(浓差极化)，用韦伯阻抗ZW[10]表示。根据上述分析建立锂电池等效电路模型，如图2所示，其中Vo和Vocv为锂电池端电压和开路电压。

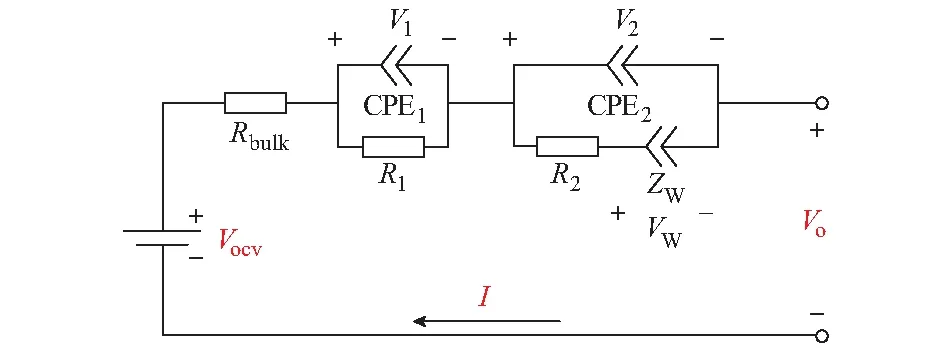
图2 锂电池分数阶阻抗模型Fig.2 Fractional-order impedance model of lithium-ion battery

引入分数阶微积分来描述常相位元件，即

(1)

式中:C为系数且C∈R;r为分数阶阶次且r∈[-1,1]。当r=0时，分数阶元件相当于电阻；当r=1时，分数阶元件相当于电容；当r=-1时，分数阶元件相当于电感。

锂电池模型中常相位元件和韦伯阻抗模型为：

(2)

式中：C1，C2，W为系数且C1，C2，W∈R;α1,α2,β为分数阶阶次且α1,α2,β∈[0,1]。

为简化模型表达，将Δr作为微积分算子，即

(3)

式中：t0和a分别为积分上、下限；τ为积分变量。

电流电压参考方向如图2所示，分数阶元件端电压为V1，V2，VW，由等效电路模型分析可知：

(4)

量测方程为：

Vo=Vocv-V1-V2-IRbulk

(5)

其中开路电压Vocv的计算常以查表方式进行。

结合式(4)和式(5)，选取分数阶元件端电压和SOC为状态量，即x=[V1,V2,VW,SSOC]T，可得到锂电池分数阶模型的状态转换方程和量测方程为：

(6)

γ=[α1α2β1]

(7)

(8)

(9)

y=Vo

(10)

(11)

D=[-Rbulk]

(12)

式中：QN为锂电池容量。

根据随机系统理论将上述方程离散化，并引入Grünwald-Letnikov分数阶理论定义[20-21]，即

(13)

(14)

(15)

式中：Ik为k时刻锂电池输出端电流；xk为k时刻状态量；yk为k时刻锂电池外部端电压值；wk-1为k-1时刻系统过程噪声;vk为k时刻量测噪声。

2 基于FUKF的SOC估计

本文提出基于分数阶阻抗模型的锂电池SOC估计方法，针对锂电池高度非线性的工作特点，采用UKF算法估计锂电池SOC。该方法引入对非线性系统采用较高精度的无迹变换[13,22]，实现状态量的快速跟踪，具体步骤如下。

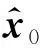
(16)

(17)

(18)

式中：Pk-1为k-1时刻误差协方差；Q为过程噪声协方差；R为量测噪声协方差。

依据比例修正采样策略获得k-1时刻采样点集ξi,k-1和权系数Wi。

(19)

(20)

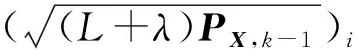
ξi,k-1经过非线性变换f(·)传播，则

(21)

(22)

Cov(xk-1,Δγxk|Yk-1)=

(23)

其中,a2=aaT;Yk-1=[y1,y2,…,yk-1]，yk-1为k-1时刻实际端电压值。

(24)

(25)

ξi,k|k-1经过量测方程h(·)非线性传播后，则

(26)

Cov(yk|Yk-1)≈Py,k|k-1=

(27)

Cov(xk,yk|Yk-1)≈Pxy,k|k-1=

(28)

计算互协方差阵Pxy,k|k-1与系统量测估计自协方差Py,k|k-1比值得到卡尔曼增益矩阵Kk，结合k时刻的实际量测信息yk更新状态量和协方差，完成k时刻最优估计,即

(29)

(30)

(31)

3 实验与数据分析

本文实验对象为中聚能源生产的磷酸铁锂电池单体，额定容量为20 Ah，电池单体截止电压上、下限分别为3.68 V和2.5 V。附录A给出所建立的锂电池测试平台，主要由LAND锂电池测试系统CT2001D、恒温箱、计算机组成，锂电池测试系统采样频率设置为1 Hz，实验环境温度设置为25 ℃。实验内容包括10 A恒流放电实验和动态压力测试工况。另外，实施了静态容量测试、Vocv-SOC测试和混合动力脉冲特性测试，用来获取锂电池开路电压Vocv真值和模型参数。在MATLAB仿真平台上对实际实验平台记录数据按照时间顺序逐点读取，验证本文模型准确性和SOC估计算法的有效性，SOC参考值由采集数据基于安时积分法获得，如式(32)所示。

(32)

式中：SSOC,init为锂电池SOC初始量。

3.1 参数辨识

锂电池电化学阻抗谱需要电化学工作站额外完成，其等效电路模型参数无法实时获得。本文在室温下对锂电池进行混合动力脉冲特性(hybrid pulse power characteristic,HPPC)测试，利用最小二乘遗传算法[23]对其在不同SOC区间的电压响应进行拟合。最小二乘遗传算法的基本思想是，将参数辨识过程模拟为生物个体的进化过程，利用遗传操作(复制、交叉、变异)生成新个体，通过适应度函数逐步淘汰适应值低的解。附录B给出锂电池SOC为50%时的电压响应，其电压响应可分为4个部分，分别表征锂电池电化学反应过程中的欧姆极化、SEI输运现象、活化极化和浓差极化现象。

在参数辨识过程中需要查表获知开路电压Vocv，而锂电池工作特性受多重因素影响，包括放电深度、负载情况、环境温度等。因此，锂电池的开路电压Vocv与SOC呈强非线性[24]。本文选择恒流充放电间歇法，将锂电池充满并静置2 h，然后对锂电池实施放电脉冲并保持ΔSSOC为10%，循环至放电截止电压，静置2 h后实施充电脉冲，分别获取放电和充电过程中SSOC=10i；i=0,1,…,10时的开路电压离散序列，取其均值得到Vocv数据。为保证Vocv-SOC曲线的单调性，本文采用分段三次Hermite插值法，对开路电压离散序列进行插值处理，附录C给出锂电池Vocv-SOC关系曲线。与高次拟合相比，Hermite插值理论具有分段插值特点并保证一阶连续导数，减小误差在整个定义域内的影响，避免造成病态曲线。

3.2 恒流放电实验

为验证锂电池分数阶阻抗模型的准确性，本文进行恒流放电实验，放电电流为10 A。同时在辨识模型参数基础上，选择本文模型IM1与文献[10]中分数阶阻抗模型IM2和文献[12]中一阶RC网络等效电路模型(用1RC表示)对比，图3为实际量测电压和模型预测端电压绝对误差曲线。

图3 10 A恒流放电测试端电压误差Fig.3 Estimated terminal voltage error under 10 A constant current test

由图3可知，本文所用分数阶阻抗模型准确性相比IM2模型和1RC网络模型有一定提高，端电压估计误差基本维持在±5 mV误差带以内，并且能较好地跟踪实际量测值。

一阶RC网络等效电路模型因其计算量适中，常与非线性滤波器UKF联合进行锂电池SOC估计。而锂电池分数阶阻抗模型描述其动态特性更为准确，常基于FKF算法进行SOC估计。因此，本文选取上述两种方法作为本文的对比算法具有一定的代表性。为验证算法的跟踪性能，选取状态量SOC初始值与真实值相差20%，初始估计方差阵P0选取为单位阵，其估计值对比如图4所示，附录D给出恒流放电实验中不同算法SOC估计绝对误差对比。

图4 恒流放电实验中，SOC参考值与FUKF，FKF，UKF算法估计值对比Fig.4 Comparison between estimation values of FUKF, FKF and UKF algorithms and SOC reference value under constant current test

由图4可知，基于分数阶阻抗模型的FUKF和FKF算法均能快速跟踪SOC参考值，而基于一阶RC网络等效电路模型的UKF算法跟踪速度较慢。在精度方面，定义为输出稳定后与参考值的最大误差。采用FUKF算法估计绝对误差最终保持在1%以内，较UKF算法(1.5%)和FKF算法(2.5%)有一定提高。

为进一步验证FUKF算法的适用性，在恒流放电实验后对其进行了锂电池恒流(10 A)充电实验，附录E给出恒流充电实验下SOC估计结果对比，基于分数阶阻抗模型的FUKF算法SOC估计误差保持在1%以内，优于UKF算法(1.5%)和FKF算法(2.5%)。

3.3 动态压力测试工况

对磷酸铁锂电池采用循环动态压力测试(dynamic stress test,DST)工况，以做进一步数据分析，DST测试中系统采集到的端电压Vo和负载电流I如附录F所示。图5为锂电池DST测试数据在UKF算法、FKF算法以及本文提出的FUKF算法的作用下的SOC估计曲线，与安时积分法获得的SOC参考值进行比较，附录F给出锂电池DST测试中不同算法SOC估计绝对误差对比。

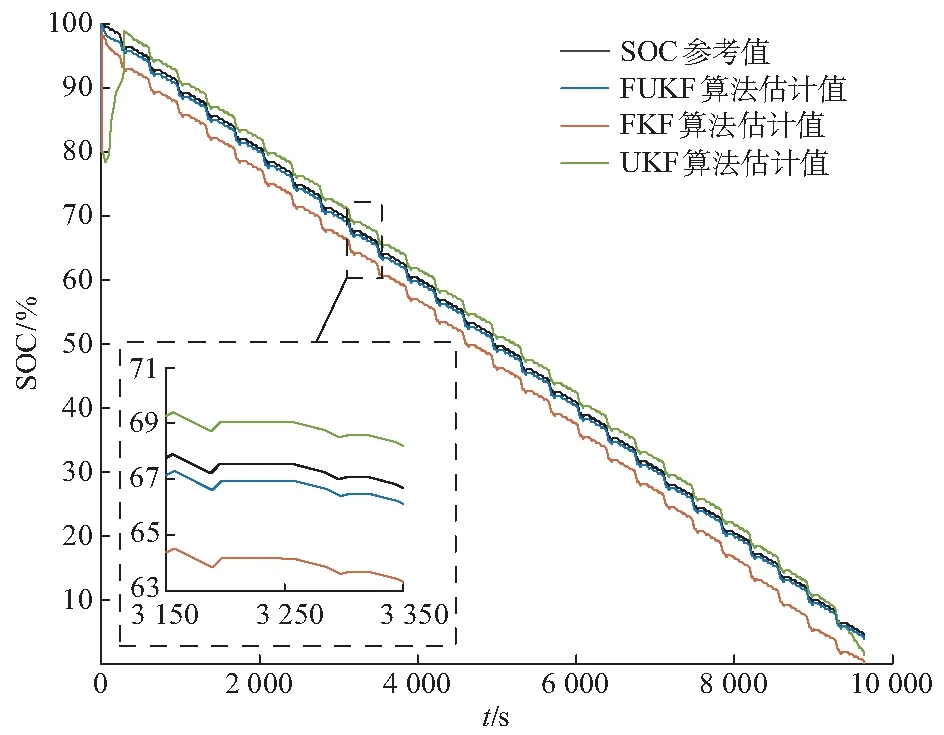
图5 动态压力测试工况中，SOC参考值与FUKF，FKF，UKF算法估计值对比Fig.5 Comparison between estimation values of FUKF, FKF and UKF algorithms and SOC reference value under dynamic stress test

由图5可知，FKF算法能够较快地跟踪锂电池SOC变化，最大估计误差为3.5%；UKF算法估计误差为1.5%，能较准确地估计锂电池SOC，但跟踪速度较慢；FUKF算法通过准确的分数阶阻抗模型和UT的共同作用，误差维持在1%以内，较上述两种算法有效提高了估计精度。另外，FUKF算法在预测步中包含了历史状态量估计值和协方差矩阵的权值求和分量，在开始阶段状态量估计值与真实值存在较大偏差时能够快速靠近真实状态，因而具有更快的跟踪速度。