社会困境下双重度偏好社团网络合作涌现研究

范如国，杨维国，张应青，崔迎迎

(1. 武汉大学经济与管理学院 武汉 430072; 2. 贵州财经大学管科学院 贵阳 550025)

社会困境常常是指这样一种情境：与采取合作行为相比，当个体采取背叛行为时往往能够获得更高的收益，但会对他人造成伤害，从而造成个体理性与集体理性的冲突[1-2]。公益事业捐款、道德滑坡、环境污染、公共地悲剧、志愿者困境、公共产品供给等被称之为典型的“社会困境”问题[3]。但是从人类社会来看，在存在大量具有目的性与自利性个体的复杂社会网络中，合作行为普遍存在，自利性主体之间既合作又竞争的博弈行为构成了社会发展和演化的基本动因。因此，人们不禁疑惑：个体自利性假设前提下合作行为是如何产生？又是怎样的机制使得合作稳定存在？为探索这一问题的答案，来自生物学、社会学、心理学、物理学、经济学、神经学以及政治学等不同学科和领域的学者们针对这一问题展开了深入的研究和讨论。

1 合作涌现机制

大量的研究表明博弈论以其清晰的数学表达和完备的公理化体系，为分析社会困境中个体理性行为以及个体间合作、冲突、协调关系的演化提供了理论框架。如囚徒困境博弈(Prisoner’s dilemma game)和公共品博弈(public goods game)是典型的描述两人和多人博弈的博弈模型，个体均以自身利益最大化作为自身的决策依据。文献[4]总结认为除了自然选择和遗传变异外，直接互惠、间接互惠、群体选择、惩罚等机制可为社会困境下合作行为的产生提供理论解释[5-7]。

有别于上述机制，空间互惠从个体间局部交互所形成的空间结构出发，发现在不存在额外的惩罚或声誉机制下，空间结构的聚集能够促成合作策略簇的形成，有效抵御不合作行为的入侵，从而促进合作行为的演化[8]。当前基于规则网络、小世界网络、无标度网络等空间结构的演化博弈已经得到较为深入的研究，其涉及到的博弈模型有囚徒困境博弈、雪堆博弈和公共品博弈等[9-11]。近年来，一些学者也关注到社会网络“社团结构”演化博弈方面的研究。所谓社团，是指由一组具有某种共同属性或起某种相似作用的节点组成的节点子集合，子集合内部连接稠密，各子集合间连接稀疏[12]。文献[13]发现结构异质性会调节社团结构对合作的影响，即低异质性的社团网络对合作产生负面影响，高异质性的社团网络对合作有积极作用。文献[14]认为复杂社会网络中的个体具有多维度属性特征，个体间的连接是基于属性的多元匹配，从而最终实现了社团“物以类聚，人以群分”的网络化表达，通过对比在无标度网络和社团网络的演化博弈结果，发现“社团结构”之所以可以促进合作行为涌现的微观机制在于社团网络中存在大量的完备三方组，从而打破了无标度网络中处于结构洞上的中间人为了获得更高收益，而控制其余两方采取不一致策略而形成的低合作水平的困境。

从上述研究可知，研究复杂社会网络中的合作行为及其机制，不能忽视“社团结构”特性，需要在更加贴近社会网络真实结构的网络模型上展开分析。但从现有研究来看，社团网络的演化博弈分析尚存在一定的不足：现有研究主要基于不随时间改变的静态社团网络来分析社团结构对合作涌现的内在机制，较少关注博弈动力学与社团网络拓扑结构的“共演化”。“共演化”是网络演化博弈重要的属性之一[15]。为了实现自身利益最大化，理性决策个体会根据博弈收益来动态调整社会关系，以期剔除那些低于预期收益的连接对象，而社会关系的改变又会进一步影响未来的博弈关系和收益，进而形成一种动态的反馈机制，如Facebook网络中新朋友的加入、企业合作网络中合作伙伴的更替、科研合作网络中合作对象的改变等。博弈与网络结构的“共演化”包括三个要素：博弈本身、与博弈策略共演化的属性(如社会关系的调整)、共演化的时间尺度[16]。因此，本文针对现有研究的不足，从动、静两个方面来系统分析社团合作涌现的内在机制。其中，静态社团网络主要关注社团内、外部连接密度的影响。社团内、外部连接密度反映的是社团内和社团间连接的紧密程度，紧密程度越高，表示整个网络“融合”的程度越大，反之，则越孤立，在一定程度上也反映了社团内和社团间信息、资源的流通速率以及学习的效率。而在动态社团网络中，主要考察策略与结构共演化时间尺度的影响。共演化时间尺度反映的是个体依据博弈结果调整社会关系的频率或时间窗，时间尺度越短，表明个体对博弈对象缺乏耐心，一旦对方带来的收益小于自己的预期，则不再与其合作，通过频繁更换博弈对象来寻求自身利益的最大化，而时间尺度越长则表明个体对博弈对象的耐心较高，在较长的时间窗下都不会随意更换自身的博弈对象。

2 基于双重度偏好的社团网络演化博弈模型

2.1 基于双重度偏好的社团网络模型

本文为了更好体现出社团网络“社团结构”特性，采用的社团网络是基于社团内节点度和社团间节点度的偏好连接形成的社团网络模型[17]，以下简称双重度偏好社团网络(community network based on double-degree-preference)。使用社团内优先连接机制的动机跟许多增长型网络模型一样，并且社团间的优先连接机制在许多真实的社团网络也有体现。例如，在科研合作网中，跨学科研究人员更有意愿学习未知领域的知识，与单一学科的研究人员相比，他们具有较强的合作欲望。同样，在朋友网中亦是如此，拥有不同社团间联系的人更容易与形形色色的人交朋友。这样的现象不胜枚举，因此，社团间的偏好连接具有现实背景。

一个具有M个社团的社团网络构建过程如下：

1) 初始网络。初始时刻，每个社团分别分m0(m0＞1)个个体组成的全局耦合网络，然后每个社团内部随机与其余M-1个社团连接M(M-1)/2条边。

2) 节点增长。每一时间步，新节点随机加入某个社团。然后该新节点与同一社团j内的m(1≤m≤m0)个节点建立m条社团内的连边，以α的概率与其他M-1个社团内的节点建立n(1≤n≤m)条社团间的连边。

3) 偏好连接。基于社团内的节点度和社团间的节点度的偏好连接。

社团内的偏好连接：当新节点与同一社团j内的节点连边时，节点i被选择的概率为：

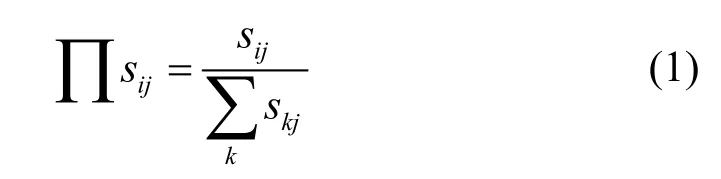
式中，sij表示节点i在社团j内的节点度，也即是不包括节点i与其他社团间连边的度值。

社团间的偏好连接：当新节点与不同社团的节点连边时，社团k(k≠j)内的节点i被选择的概率为：

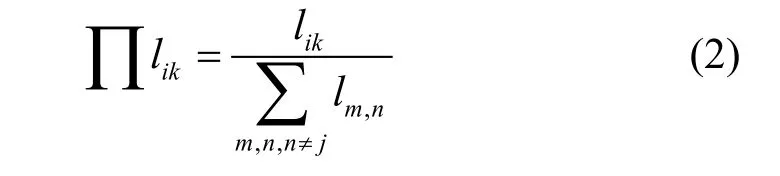
式中，lik表示节点i在社团k外的节点度，也即是不包括节点i与社团k内连边的度值。

4) 网络增长。t时间步后，该机制会形成一个有Mm0+t个顶点，期望为E{[Mm0(m0-1)+M(M-1)]/2+mt+integer(αnt)}条边的社团网络。参数α和n控制着社团间的边数和社团内的边数的比例，m/n和α共同决定了社团网络中“社团结构”的显著程度，m/n越大以及α越小，表明“社团结构”越明显。

2.2 双重度偏好社团网络下的演化博弈模型

基于前文分析可知，尽管当前“社会困境”问题常常表现为一个多人困境，但究其本质，可以看成是一个多人的囚徒困境博弈。囚徒困境作为经典的博弈论模型(如表1所示)，其中C表示博弈主体采取合作策略；D表示采取背叛策略，参数满足T＞R＞P＞S和2R＞T+S。

表1 囚徒困境博弈支付矩阵

囚徒困境博弈具有如下特性：1) 囚徒困境能够清晰地阐释出个体理性与集体理性的矛盾和冲突。在囚徒困境博弈中，如果每个个体出于自身利益最大化的个体理性目标(即获得收益T)，就倾向于选择背叛或搭便车策略，而最终使得总体收益降到最低(2P)，从而背离了集体理性的帕累托最优结果(2R)。2) 囚徒困境蕴含了更为微观的“贪婪”和“担心”的动机因素[18]。“贪婪”是诱惑人们做出背叛或搭便车决策的重要动机因素，可用单方背叛收益与相互合作收益之差来进行表示(T-R)，而“担心”反映的是当对方如果选择背叛而自己应该如何反应的心理动机，为了避免损失和被剥削，个体往往会选择与对方一致的策略，“担心”可用相互背叛的收益与单方合作收益之差来进行表示(P-S)。

弱囚徒困境博弈是囚徒困境博弈的简化模型，因只包含一个自由变量，能够极大地简化模型分析。因此，本文将模型中各参数设定为：2≥T=b＞1，R=1，S=P=0，b称为背叛诱惑值。

策略更新规则使用相邻节点学习的费米函数，本文采用基于累积收益的策略更新规则[19]：

式中，si、sj分别表示主体i和j采取的策略；Pi、Pj分别表示主体i和j本轮的累积收益；k表示环境噪声。k越大，个体的理性程度就越低，学习收益低的邻居节点的策略的概率就越大。k→∞时转化为随机模仿规则，即以抛硬币的方式(正或反概率均为1/2)决定是否采取邻居节点的策略。

2.3 静、动态双重度偏好社团网络结构的演化规则

静态双重度偏好社团网络上的演化博弈的步骤为：初始时，每个博弈主体以合作或背叛策略均匀分布在双重度偏好社团网络上；每演化时间步，每个主体与其直接邻居同时参与“弱囚徒困境”博弈，并根据支付矩阵(表1)计算相应的收益进行累积，以此作为该主体本轮博弈的总收益；最后，每个博弈主体根据式(3)进行策略更新，直至策略稳定后停止博弈和策略更新。

动态双重度偏好社团网络上的演化博弈与上述静态的不同之处在于，博弈主体每经过S轮博弈和策略更新后还要进行网络结构调整，分为断边和重连过程，具体为：主体i在其持背叛策略的邻居节点中随机选出某个主体j与其断边，再从主体j的邻居中随机选出一个与主体j在一个社团内的主体k进行连边。在此过程中，倘若主体i的邻居均为合作策略或者主体j的度为1，或者主体j的邻居节点均不与其在同一社团，那么主体i放弃此次断边重连的机会。

3 仿真实验

本文设定双重度偏好社团网络的规模N=500，社团个数M=5，初始全耦合网络m0=3，新节点与同社团的连边数目m =2，新节点与不同社团的连边数目n和概率α为可变参数。

3.1 连接密度对合作涌现的影响分析

通过调节可变参数n，α，可生成不同内、外部连接密度的社团网络，以此来分析社团网络中连接密度对合作涌现的影响。合作涌现一般可以通过合作水平来衡量，其反映的是群体中采取合作策略的比例，可用 fc(fraction of cooperators)表示。

仿真实验步骤如下：

1) 构建(n=1,α=0)，(n=1,α=0.5)，(n=1,α=1)和(n=2,α=1)4种参数情境下的双重度偏好社团网络，随机分配个体的初始策略，使网络总的初始合作水平fc=50%；

2) 每演化时间步，每个个体与相邻节点同时进行“弱囚徒困境”博弈，并根据博弈收益结果进行策略更新，策略更新中的环境噪声k取0.1，系统演化总时长设定为T=5 000步，取最后500步稳定状态的合作频率的均值作为合作水平 fc，即其中， Nc(t)为第t演化时间步的合作者数量；

3) 为了剔除实验过程中随机数的影响，重复上述实验100次，并取其平均值作为最终结果，仿真结果如图1所示。

图1 连接密度对合作涌现的影响

从图1合作水平fc的总体趋势来看，合作水平均随背叛诱惑值b的增加先保持不变，当背叛诱惑值超过一定阈值后，呈持续下降趋势，且连接密度较大的社团网络合作水平下降比密度较小的社会网络要快。具体来看，当背叛诱惑值较小时(1≤b≤1.48)，无论社团网络的连接密度如何，总是呈现出全局合作的最优状态，而一旦当背叛诱惑值超过一定的阈值时(1.48 ＜ b≤2)，合作者将无法完全取代背叛者，开始出现背叛者入侵合作者的情形，呈现合作者与背叛者共存的演化结果，致使总合作水平下降，且社团内以及社团间的连接密度越大时(n=2,α=1)，合作水平下降最快且幅度最大。出现上述结果的原因在于当背叛诱惑值b较小时，合作策略在重复的博弈过程中会成为占优策略，通过不断形成紧密的合作团簇来抵御背叛者入侵和转化背叛者，从而使得合作策略成为最终的群体选择。而当背叛诱惑值逐渐增大时，且超过一定阈值时，总有一些背叛者试图冒险通过“搭便车”的形式来获得高收益，且当社团内以及社团间的连接密度较大时，增加了背叛者入侵的通道，从而逐渐瓦解合作者紧密形成的合作团簇，使得总合作水平逐渐下降。但从总体上看，即使当背叛诱惑值达到最大(b =2)，合作者依然是社团群体中的主要力量(73%≤fc≤76.5%)，这也说明了复杂社会网络的“社团结构”确实起到了凝聚和团结合作的作用。

进一步地，可以从社团网络的中观结构来分析合作水平的变化趋势，如网络平均度、模块度以及度相关系数，结果如表2所示。

表2 不同连接密度下社团网络结构参数表

从表2可以看出，首先，社团网络的平均度与连接密度呈同方向变动，而早些基于规则网络、星型网络和无标度网络的研究发现，高的平均度往往导致低的合作水平[20]，这就从一方面解释了连接密度较大的社团网络产生合作水平较低的原因。再者，社团网络的模块度与连接密度呈反方向变动。社团内、外部连接的增多，使得整个社团网络呈现“融合”的状态，从而让社团内节点间的紧密程度相对降低，在博弈演化过程中不易形成合作团簇，这也从另一方面解释了合作水平较低的现象。最后，网络的度相关系数绝对值与连接密度呈反方向变动，一定程度上反映了网络的异质性有利于合作涌现[21]。

3.2 策略与结构共演化对合作涌现的影响分析

选取n=1，α=0.5所形成的双重度偏好社团网络，用来对比分析静态社团网络和动态社团网络的差异以及策略与结构共演化机制对合作涌现的影响。合作水平采用fc来衡量，仿真实验设计如下：

1) 随机分配个体的初始策略，使初始合作水平fc=50%；

2) 在静态社团网络和动态社团网络中，每演化时间步，每个个体与相邻节点同时进行“弱囚徒困境”博弈，并根据博弈收益结果进行策略更新；此外，动态社团网络中策略与结构共演化的时间尺度取S=5，即所有个体进行5次演化时间步后，依据断边重连机制来调整自身的社会关系。

3) 计算静态和动态社团网络中博弈进行稳定状态下的合作频率fc。仿真结果如图2所示。

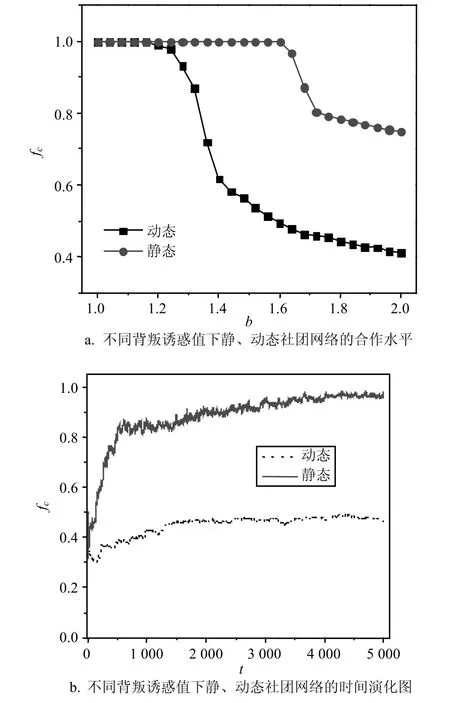
图2 不同背叛诱惑值下静、动态社团网络的合作水平及其随时间演化图

从图2可以看出，动态社团网络的合作水平fc随着背叛诱惑值b的增大，总体上是劣于静态社团网络，且当背叛诱惑值b＞1.6左右时，动态社团网络的总体合作水平fc＜0.5，即社团群体中的大多数人选择成为背叛者，而一旦群体中背叛者占多数的现象发生意味着群体合作的困境将会产生。为何在断开与背叛者连接并寻找更优连接的策略与结构共演化机制下，社团网络的整体合作水平反而比没有这种机制条件下的静态社团网络更低呢？为了揭示策略与结构共演化对合作涌现的影响机制，本文进一步从共演化时间尺度的角度来系统分析和阐释。

3.3 策略与结构共演化对合作涌现的影响分析

同样基于n=1,α=0.5参数情景下形成的双重度偏好社团网络，来进一步分析动态社团结构策略与结构共演化机制下时间尺度S对合作涌现的影响。合作涌现除用合作水平 fc外，还将从策略的稳定性(strategy stability)来衡量，仿真实验设计如下：

1) 随机分配个体的初始策略，使初始合作水平fc=50%；

2) 每演化时间步，每个个体与相邻节点同时进行“弱囚徒困境”博弈，并根据博弈收益结果进行策略更新，策略与结构共演化的时间尺度取S=5、S=10、S=20、S=30、S=50五种不同情况，S=5 000，即静态社团网络，作为动态社团网络的基准对比。

3) 策略的稳定性，借鉴文献[22]的研究，在每个背叛诱惑值下，根据节点演化稳定后采取的策略，将节点分为三类：纯合作者(pure cooperators, PC)，即最后500步均采用合作策略；纯背叛者(pure defectors, PD)，即最后500步均采用背叛策略；不断改变策略的骑墙者(fluctuating)，并将节点最后一步采取的策略赋予骑墙者，纯合作者、纯背叛者以及骑墙者占全部节点的比例，分别用pc、pd、fl表示。仿真结果如图3所示。

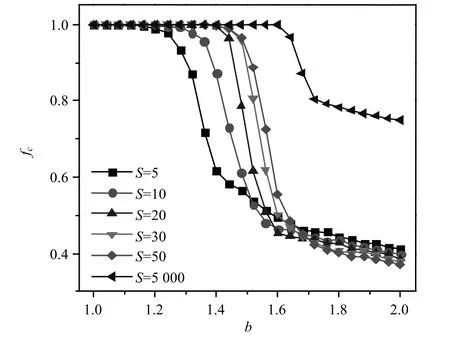
图3 时间尺度对合作涌现的影响

从图3可以看出：动态社团网络下的合作水平fc对背叛诱惑值b的敏感程度高于静态社团网络，总体上呈现随背叛诱惑值先迅速下降后逐渐平稳的态势。具体来看，当b＞1.2左右时，动态社团网络的合作水平就开始出现下降，且时间尺度越小其受背叛诱惑值的阈值越低，而只有当b＞1.6左右时，静态社团网络才开始出现合作水平的下降，且其下降幅度很快就趋于平缓。动态网络中策略与结构共演化的时间尺度对合作涌现的影响是由背叛诱惑值和时间尺度来共同决定的，当b＜1.6左右时，时间尺度越大情形下的合作水平越高，而当b＞1.6左右时，时间尺度越小越有利于合作。

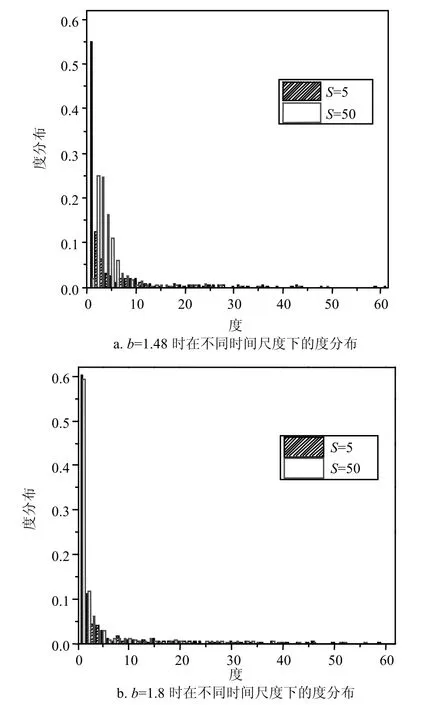
图4 不同时间尺度下的度分布

出现上述现象的主要原因在于：首先，在动态社团网络策略与结构共演化过程中，如果频繁地断开与背叛者的连边，会使得网路中出现了大量度很小的个体，例如在b=1.48和b=1.8的动态社团网络中(如图4所示)，在稳定状态时网络中竟出现了60%～70%的度为1或2的个体，而这些度小的节点一般处于网络的边缘，策略更新时很难学习其他节点的合作策略，最终导致网络整体合作水平的降低。进一步地，从不同背叛诱惑值下度分布差异来看，当b=1.48时(如图4a所示)，时间尺度较小(S=5)情形下的小度个体远远多于时间尺度较大的情形(S=50)，因而其合作水平远低于时间尺度较大的情形；而当b=1.8时(如图4b所示)，时间尺度S=5的小度个体略低于S=50，因而其合作水平略高于时间尺度较大的情形。

图5 不同时间尺度下的策略稳定性

其次，从策略的稳定性来看(如图5所示)，在静态社团网络中，纯合作者占比是随背叛诱惑值而逐渐走低，纯背叛者几乎不存在，取而代之的是存在大量的骑墙者。而在动态社团网络中，随着背叛诱惑值的增大，是呈现纯合作者、纯背叛者和骑墙者共存的演化结果，且骑墙者远低于静态社团网络，而纯合作者又高于静态社团网络。综合来看，尽管动态社团网络的合作水平低于静态社团网络，但动态社团网络中策略稳定性要强于相应的静态社团网络。进一步地，从不同时间尺度下的策略稳定性来看，当b＜1.6左右时，时间尺度较小(S=5)情形下的纯合作者较少，且纯背叛者和骑墙者的数量远多于时间尺度较大(S=50)的情形，因而其策略的稳定性要弱于S=50的情形，使得其合作水平在较低的背叛诱惑值下处于较低水平；而当b＞1.6左右时，时间尺度较小(S=5)情形下的纯背叛者远少于时间尺度较大(S=50)的情形，使得其合作水平在较大的背叛诱惑值下又有可能高于时间尺度较大的情形。

最后，从不同时间尺度下不同类型边，即C-C型(合作者与合作者)、C-D型(合作者与背叛者)、D-D型(背叛者与背叛者)，随演化的变化情况来看(如图6所示)，在背叛诱惑值较小b=1.48时，d-d links相差不大，c-c links在S=50下动态社团网络中达到最高，静态社团网络次之，S=5下的动态社团网络最少，而c-d links是S=5下的动态社团网络最高，静态社团网络次之，S=50下的动态社团网络最少，表明此时S=5下的动态社团网络中较少的c-c links和较多的c-d links使得其合作水平最低；而在背叛诱惑值较大b=1.8时，c-c links在S=5下动态社团网络中达到最高，S=50下的动态社团网络次之，静态社团网络最少，而c-d links和d-d links是静态社团网络远高于动态社团网络(S=5和S=50)，且S=50下的动态社团网络略高于S=5下的动态社团网络，表明此时虽然静态社团网络c-c links数量较少但能凭借较多的c-d links来获得更高的合作水平，于此同时S=5下的动态社团网络中较高的c-c links，以及较低的d-d links和c-d links使得其合作水平略高于S=50的情形。

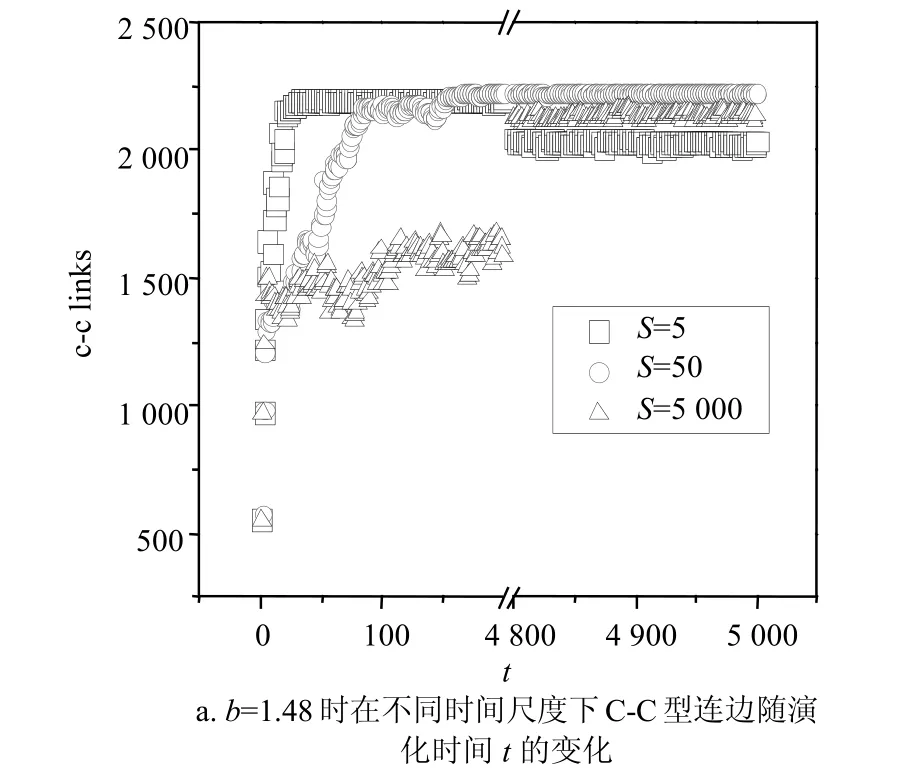
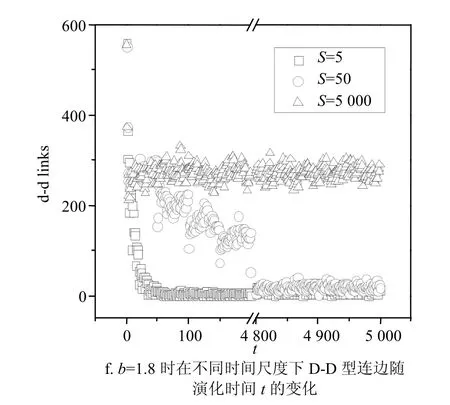
图6 不同时间尺度和背叛诱惑值下连边类型随演化时间步t的变化关系

综合来看，可以得到两点重要结论：1) 尽管静态社团网络合作水平fc在数值上明显高于动态社团网络，但其合作演化的策略构成、策略稳定性及其演化动态性存在显著差异。具体来说，首先，静态社团网络中存在大量的骑墙者且纯合作者较少，而动态社团网络中呈现纯合作者、纯背叛者和骑墙者共存的演化结果，且骑墙者数量远远小于静态社团网络，表明动态社团网络中策略稳定性要强于相应的静态社团网络；其次，在策略与结构共演化机制下，动态社团网络中的个体能够通过断开与背叛者的连接来调整自身的社会关系，以期获得更高的收益，因而动态社团网络在不断调整社会关系的过程中，能够形成大量的合作与合作连边(c-c links)，从而有效构成合作团簇，迅速形成抵御背叛者入侵的群体能力，且当调整的时间尺度越小，其形成合作团簇所需的演化时间越短。2) 动态社团网络中策略与结构共演化的时间尺度对合作涌现的影响呈现复杂的、相对优劣互转的变化趋势，具体表现为在低背叛诱惑值下时间尺度越小越不利于合作，而在高背叛诱惑值下时间尺度越小越有利于合作。其主要是由于在低背叛诱惑值下，如果频繁地断开与背叛者的连边，会使得网路中出现了大量度很小的个体，而这些度小的节点一般处于网络的边缘，策略更新时很难学习其他节点的合作策略，从而形成较多的纯背叛者，导致时间尺度越小其合作水平越低；而在高背叛诱惑值下，大量的个体开始成为背叛者，如果不迅速断开与背叛者的连接，将会加速背叛策略的扩散，因此只有频繁地断开与背叛者的连边，才能在一定程度上遏制住背叛策略的持续扩散，因而此时时间尺度越小越有利于合作。

3.4 噪声对合作涌现的影响分析

策略更新过程中的噪声对合作涌现的影响分析是复杂社会网络演化博弈中的重要问题[23]，具有较高的理论价值和实践指导意义，主要是分析个体的非理性程度是如何影响合作行为及其演化过程。因此，本文进一步地从噪声角度系统地分析静态社团网络和动态社团网络的合作演化过程，仿真结果如图7所示。

图7 不同噪声下静态、动态社团网络的合作水平

从图7可以看出，除了在低背叛诱惑值b=1.48下静态社团网络一直维持在最高合作水平外，噪声对静态和动态社团网络合作涌现的影响是单调的，且适度引入噪声能够显著提高合作水平，这与在格子网络上得到的结论相类似[24]。进一步来看，当背叛诱惑值b=1.8且噪声较小时，静态社团网络的合作水平高于动态社团网络，而在噪声较大时，动态社团网络的合作水平超过了静态社团网络。这是因为当背叛诱惑值较大且噪声较高时，动态社团网络中的个体能够迅速断开与背叛者的连边，同时高噪声的引入进一步提高个体学习合作策略的可能性。

4 结 束 语

本文从当前复杂社会网络中最突出的“社团结构”特征出发，并考虑个体的双重度连接偏好，基于经典的囚徒困境博弈和累积收益策略更新规则，构建社会困境下双重度偏好的社团网络演化博弈模型，系统研究静态社团网络外部连接密度、动态社团网络中策略与结构共演化时间尺度以及策略更新中噪声对合作涌现的影响及其作用机理，并得到了一些有价值、有意义的结论。研究发现：1) 连接密度对合作涌现的效率具有负向影响。当社团间外部连接的增多，反而会降低社团内节点间的紧密度，不利于演化过程中合作簇的形成；2) 尽管静态社团网络合作水平在数值上是明显高于动态社团网络，但其合作演化的策略构成、策略稳定性及其演化动态性存在显著差异。静态社团网络中存在大量的骑墙者且纯合作者较少，而动态社团网络中呈现纯合作者、纯背叛者和骑墙者共存的演化结果，且骑墙者数量远远小于静态社团网络，表明动态社团网络中策略稳定性要强于相应的静态社团网络；3) 动态社团网络中策略与结构共演化的时间尺度对合作涌现的影响呈现复杂的、相对优劣互转的变化趋势，具体表现为在低背叛诱惑值下时间尺度越小越不利于合作，而在高背叛诱惑值下时间尺度越小越有利于合作，这主要是因为在低背叛诱惑值下，如果频繁地断开与背叛者的连边，会切断合作策略扩散的回路，同时也会因为大量网络边缘小度个体的存在使得合作策略的扩散难度增加，而在高背叛诱惑值下，大量的个体开始成为背叛者，需要加速断开与背叛者的连接，才能在一定程度上遏制住背叛策略的持续扩散。4) 策略更新过程中噪声对静态和动态社团网络合作涌现的影响是单调的，且适度的引入噪声能够显著提高合作水平。本文的研究对进一步完善基于“空间互惠”来破解社会困境的理论构建起到推动作用，对于指导群体合作、资源困境、环境污染、公共地悲剧等具有一定的实践价值。