基于EVT法和MC模型的极限水文干旱历时计算研究

2018-12-06宋松柏张更喜

西北农林科技大学学报（自然科学版） 2018年11期

赵纬，宋松柏，张更喜

(西北农林科技大学水利与建筑工程学院，陕西杨凌712100)

干旱是世界上最主要的自然灾害之一，一直受到环境学、生态学、水文学和气象学等诸多领域的密切关注。由于干旱形成条件的复杂性和对社会影响的广泛性，干旱一般可分为水文干旱、气象干旱、农业干旱和社会经济干旱。其中，水文干旱的影响因素较气象、农业等干旱更加复杂，且更容易受到人为因素的影响。因而，其能较全面地反映区域的整体干旱状况[1]。水文干旱通常是指在一定时期内河流径流量低于临界水平而造成的水分亏缺现象。其中，亏缺量和持续时间可以分别用干旱烈度和干旱历时表示[2]。当水文干旱历时持续的时间超过河流、水库等的承载能力时，就会对农业生产和社会发展造成严重影响[3]。由于现有的实测水文序列较短，从而使得在有限实测序列中提取出的干旱序列更短。因此，上述问题给区域实际旱情和抗旱年限的确定带来了困难。在实际应用中，人们常通过严密的数学推导获取表征极限水文干旱历时的解析表达式，从而为区域水资源规划与利用、抗旱年限确定以及区域社会与经济发展计划制定等提供依据[4]。

极限干旱历时是指在一定时期内可能出现的水文干旱的最大干旱历时[5]，其计算方法是水文学家和水资源管理者共同感兴趣的问题之一。20世纪60年代末，Feller[6]应用游程理论首次推导出最大游程长度的概率分布函数。之后，关于极限干旱历时概率计算方法的研究得到了国内外学者的广泛关注。Moye等[7-8]以游程理论为基础，运用极值顺序统计量概念，经过严密的数学推导得到了计算极限干旱历时期望值和方差值的解析表达式。马秀峰等[9-10]从简单的伯努利试验出发，结合随机模拟试验，发现平稳随机序列的轮次长度服从二阶线性齐次差分方程。冯国章[11-13]用枚举法推导出独立同分布随机变量序列最大负游程长度的概率分布函数，并将其作为极限干旱历时的概率分布函数，与相同结构的年径流序列最大水文干旱历时的经验频率拟合，取得了较好的拟合效果。Sharma等[14-15]研究了不同截断水平条件下，当径流序列服从正态分布、gamma分布和对数正态分布的极限干旱历时和强度的概率分布函数。丁晶等[16]以年径流数据为基础，分析水文干旱中负轮长的变化特征，发现P-Ⅲ型分布可以用来表征负轮长的统计特性。Cancelliere等[17]假设水文数据服从周期性的简单马尔科夫链，推导出了极限干旱历时概率分布和重现期的解析表达式。袁超等[4]根据游程理论和随机变量极值理论，采用解析法和模拟法进行了极限水文干旱历时概率分布和径流序列参数的影响研究。Sharma等[18]和Panu等[19]以月、年时间尺度上的径流序列为例，运用极值理论法和马尔科夫模型研究了极限干旱历时、最大干旱强度和最大干旱烈度之间的关系。综上可知，关于水文干旱历时概率的研究虽已经取得了一些成果，但对于极值理论(Extreme value theory,EVT)法和马尔科夫链(Markov chain,MC)模型在计算极限干旱历时中的对比研究尚比较少，且缺少应用案例。为此，本研究应用游程理论(Run theory)，以黄河流域3个水文站的年径流资料为研究对象，应用EVT法和MC模型计算极限干旱历时，将计算值与实际观测结果进行对比，并采用纳什效率系数(NS)和平均绝对百分误差(MAPE)对计算精度进行评价，分析EVT法和MC模型在该流域的适用性，以期为区域干旱历时的预报提供参考和依据。

1 极限干旱历时的计算方法

1.1 EVT法

随机变量极值理论是Todorovic等[20]在1975年提出的，该方法有以下3点假设：

1) 在重现期T内，干旱发生次数的概率服从泊松分布，其概率密度函数为：

(1)

式中：P为离散事件的概率值；n为干旱发生次数；j为干旱发生次数值，取离散值；q为干旱概率；qq为前一时段发生干旱条件下下一时段发生干旱的条件概率。

2) 对干旱历时进行分析时，需要用到条件概率qq。qq可由求解径流序列的相关计算参数得到，计算公式[21]为：

(2)

式中：ρ1为一阶自相关系数，z0为标准正态变量值，ρ为积分变量。

3) 在某一游程中，干旱历时发生的概率一般服从几何分布，即：

P(L=l)=ql-1·p,l=1,2,3,…。

(3)

式中：L为干旱历时；l为干旱历时值变量，取离散值；p为不发生干旱的概率，p=1-q。

基于以上3点假设，可以得出在重现期T内，极限干旱历时的概率分布、期望及方差，即：

P(LT=i)=exp[-T·q(1-qq)qqi-1]·
[exp(T·q(1-qq)2qqi-1)-1],i=1,2,3,…。

(4)

(5)

(6)

式中：LT为极限干旱历时。对于年径流序列，i的最大取值为25，因为当i的取值大于25时，式(4)中的概率值很小可以忽略不计。因此，式(5)又可以表示为：

E(LT)=1P(LT=1)+2P(LT=2)+3P(LT=3)+
…+25P(LT=25)。

(7)

1.2 MC模型

根据Sharma等[22]对于极限水文干旱历时的定义，马尔科夫链中有关干旱事件的概率可约定如下：

q=P(d);p=P(w),

(8)

qp=P(d/w);pqq=P(w/d,d),

(9)

qqp=P(d|d,w);qqq=P(d|d,d)。

(10)

式中：d为干旱事件；w为不干旱事件；qp为前一时段不发生干旱条件下下一时段发生干旱的条件概率；pqq为前两时段发生干旱条件下下一时段不发生干旱的条件概率；qqp为前两时段中第一时段发生干旱而第二时段不发生干旱条件下下一时段不发生干旱的条件概率；qqq为前两时段发生干旱的条件下下一时段仍然发生干旱的条件概率。

根据干旱的定义，可以将干旱历时的发生概率表示为：

P(L=l)=P(w)P(d|w)P(d|d,w)·

[P(d|d,d)]l-2P(w|d,d),l=2,3,4,…。

(11)

在重现期T内，干旱发生的超越概率为1/T。如果干旱历时的发生概率≥l，则在满足二阶马尔科夫链(two-order Markov chain,MC-2)模型的条件下，公式(11)可进一步表示为：

(12)

将式(8)～(10)代入式(12)，可得重现期为T年的超越概率为：

(13)

由式(13)可得，满足MC-2模型的极限干旱历时的表达式为：

(14)

本研究中极限干旱历时的计算选用Sharma等[15]修正后的公式。因此，满足MC-2模型的极限水文干旱历时的表达式为：

(15)

式中：F为计算因子，可以通过经验绘点位置公式得到，例如F=1，1.6，2分别代表weibull、blom、hazen绘点位置公式。

当qqp=qq且qqq=qq时，MC-2模型可简化为一阶马尔科夫链(one-order Markov chain,MC-1)模型。因此，满足MC-1模型的极限水文干旱历时的表达式为：

(16)

当qp=q和qq=q时，MC-1模型可简化为零阶马尔科夫链(zero-order Markov chain,MC-0)模型。因此，满足MC-0模型的极限水文干旱历时的表达式为：

(17)

由于年径流序列具有弱相关性,因此本研究选取MC-1模型计算极限干旱历时。其中条件概率qp可由式(18)和式(19)得到，即：

(18)

qp+pp=1。

(19)

式中：pp为前一时段不发生干旱条件下下一时段也不发生干旱的条件概率。

2 径流序列的标准化处理

对于水文序列xi，经过标准化处理后得到标准水文序列ei，其转化公式为：

(20)

式中：μx和σx分别为水文序列的均值和标准差。

如果标准水文序列ei服从正态分布，则有ei=zn，那么干旱概率q可以通过标准化正态分布函数表或者下面的标准化正态概率积分得到,即：

(21)

式中：e0为标准截断水平，e0=(x0-μ0)/σx，其中x0为截断水平；zn为标准正态变量值；z为积分变量。

当标准水文序列ei服从对数正态分布或两参数gamma分布时，可以通过公式(22)或(23)变换为近似标准化的正态序列zl或zg，然后再将zl=zn或zg=zn代入式(21)中，从而得到干旱概率q。其中：

(22)

(23)

式中：Cv为水文序列的变差系数。

在本研究中，可以利用公式(24)中的Wilson-Hilferty反转换法[23]，将标准水文序列ei变换为近似标准化的正态序列z0，然后再将z0=zn代入式(21)中，从而得到干旱概率q。

Z0=(6/Cs)[(0.5Csei+1)0.333-1]+Cs/6。

(24)

式中：Cs为水文序列的偏态系数。

取不同的截断水平e0和变差系数Cv，由式(2)、(21)、(22)、(23)分别计算正态分布、对数正态分布和两参数gamma分布的标准正态值和干旱概率值，结果见表1。

表1 不同截断水平下的标准正态值和干旱概率值Table 1 Standard normal values drought probability in different threshold levels

3 实例应用

3.1 黄河流域极限水文干旱历时的确定

以黄河流域兰州、龙门、白马寺3个水文站的年径流序列为例，应用上述公式，计算基于EVT法和MC-1模型的极限干旱历时。经审查，各站资料均符合可靠性、一致性和代表性的要求，3个水文站径流序列的基本统计参数，包括均值μx、标准差σx、变差系数Cv、偏态系数Cs和一阶自相关系数ρ1均列于表2。

表2 黄河流域3个水文站年径流序列的统计参数Table 2 Statistical parameters of 3 hydrological stations in the Yellow River Basin

应用EVT法和MC-1模型，计算3个水文站在10个概率水平下的极限干旱历时，并将E(LT)与LT-ob进行对比。各测站年径流序列E(LT)和LT-ob的计算结果见表3～5。从表3～5可以看出：当干旱概率q以0.05为步长均匀减小时，标准化截断水平e0、干旱概率q和条件概率qq、qp均呈减小趋势。与LT-ob相比，EVT法计算的E(LT)的偏差值在1年之内；而MC-1模型结合weibull、hazen、和blom绘点位置公式计算的E(LT)，在有些概率水平下的偏差值达到了2年。

为了更加直观地对比分析2种计算方法的优劣，将E(LT)和LT-ob绘制在斜率为1的直线两侧。由于MC-1模型结合3种绘点位置公式计算得到的E(LT)和LT-ob的对比图趋势相似，因此本研究只将MC-1模型结合hazen绘点位置公式计算的E(LT)和LT-ob对比绘制在图1中。

由图1可以看出，各测站年径流序列的E(LT)和LT-ob点值分散在斜率为1的直线周围，这是因为对计算值进行了取整。例如：在年尺度上计算的E(LT)是4.49和4.51，分别被近似为4和5年。当计算值的范围在1～11时，即便是180个点被计算出来，但大量的点都是彼此重叠的，并且只有有限的点被绘制在图形中。在不同的截断水平下，EVT法计算的E(LT)与LT-ob的偏差在2年之内，而MC-1模型结合hazen绘点位置公式计算的E(LT)与LT-ob的偏差值在有些截断水平下则达到了3年。

表3 兰州站极限干旱历时计算值和对应观测值的比较Table 3 Comparison of calculated and observed values of critical drought duration at Lanzhou station

注：第6～9列括号内数值为计算值，括号外数值为取整值；表4，5同。

Note:The values in the parentheses are calculated values and outside are the integer values from sixth to ninth columns.The same for Table 4 and 5.

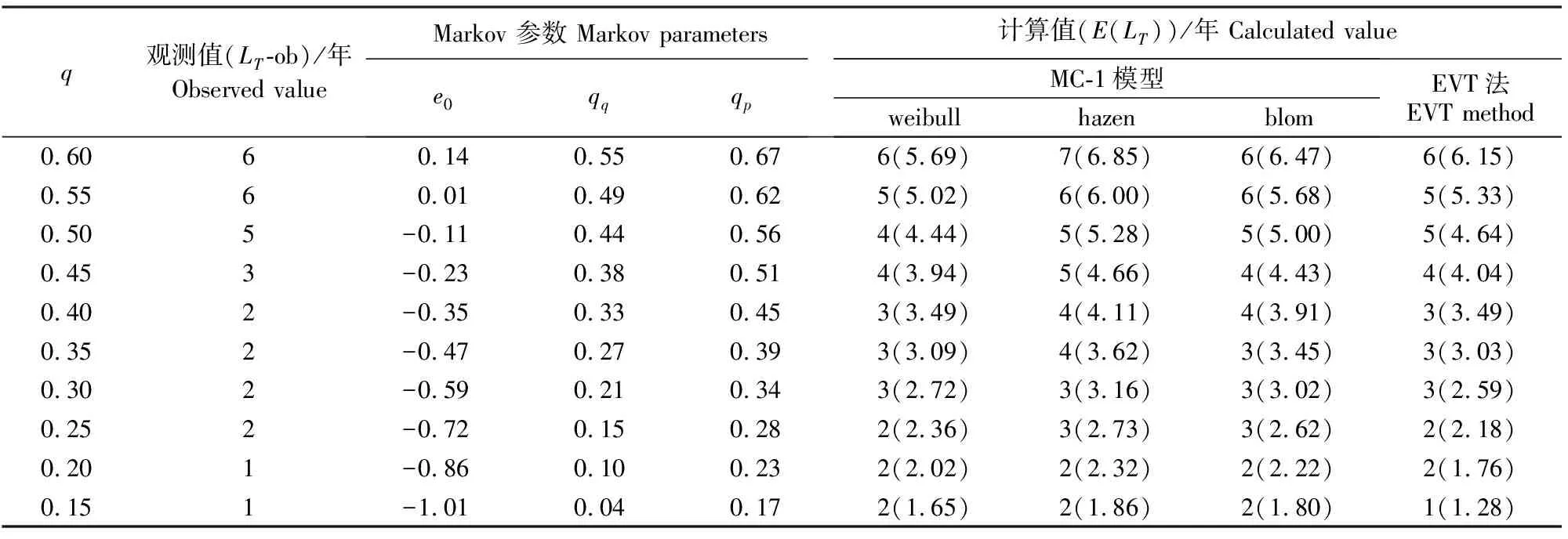
表4 龙门站极限干旱历时计算值和对应观测值的比较Table 4 Comparison of calculated and observed values of critical drought duration at Longmen station

表5 白马寺站极限干旱历时计算值和对应观测值的比较Table 5 Comparison of calculated values and observed values of critical drought duration for Baimasi station

图1 3个水文站极限干旱历时计算值与观测值的对比Fig.1 Comparison of calculated and observed values of critical drought duration at 3 hydrological stations

3.2 计算结果的精度评价

基于年时间尺度,通过MC-1模型和EVT 2种方法计算的极限干旱历时，很难从数值上判断哪种方法更加优越，故需要用NS和MAPE 2个统计量对计算结果进行评价。NS值越接近1，或MAPE值越接近0，表明预测效果越准确。

(1)纳什效率系数(NS)。计算公式为：

(2)平均绝对百分误差(MAPE)。计算公式为：

(26)

式中：Pi为计算值；Oi为实测值；Omean为实测值的平均值；N为实测干旱历时长度。

本研究将黄河流域兰州、龙门、白马寺3个水文站极限干旱历时计算精度的评价结果列于表6。

表6 3个水文站极限干旱历时计算结果的精度评价Table 6 Accuracy evaluation of predictive results for critical drought duration at 3 stations

从表6可以看出：对于兰州站而言，在年时间尺度上,EVT法和MC-1模型计算结果的NS值均超过0.824 7，并且两者很接近；其中EVT法计算的NS值达到了0.921 0，可认为其计算精度最高。同时2种方法计算结果的MAPE值也以EVT法最小。对于龙门站而言，MC-1模型结合3种绘点位置公式所得结果的NS值和MAPE值差异均比较大，其中MC-1模型结合weibull绘点位置公式时的精度评价结果与EVT法最为接近，只是EVT法的MAPE值略小于MC-1模型结合weibull绘点位置公式的值。对于白马寺站而言，EVT法和MC-1模型结合blom绘点位置公式所得结果的NS值和MAPE值较为接近，二者无明显差异。因此，从以上3个水文站的精度评价可以看出：在年径流时间尺度上，与MC-1模型相比，EVT法能够更好地用于极限干旱历时的计算。