一类新型的非线性压缩映射的不动点定理

李春平

(山西大学 商务学院公共基础部,山西 太原 030031)

0 引言和预备知识

泛函分析作为较新的一门数学分支,以其在微分方程、动力系统等各个领域应用的广泛性,在现代数学中占有重要的地位．其中,关于压缩映射的不动点理论研究尤为突出．研究内容丰富,新的成果也不断出现．不动点理论本质上就是求解算子方程Ax=x的问题,是判断方程解的存在和唯一性的主要依据．其中,Banach不动点定理(Banach压缩映象原理)[1]是泛函分析中的一个最常用、最基本的不动点存在性定理,为线性方程组的求解提供了最优的逼近程序[2],为微分方程中最重要的定理之一——Picard定理的证明提供了理论依据[3]．近年来,随着非线性微积分方程及随机算子理论等的进一步发展,人们关于不同类型非线性压缩映射的不动点讨论日益增多,如文[4-7]．本文针对一类新型的、更一般的非线性压缩映射,讨论其不动点的存在性和唯一性,还给出了相应的误差估计不等式,拓宽了定理的应用范围．

定义1[1]若(X,ρ)是一度量空间,点列{xn}是空间上的基本列(Cauchy列),是指:

ρ(xn,xm)→0(n,m→∞)．

定义2[1]若度量空间(X,ρ)中所有的基本列均收敛,则称该空间是完备的．

定义3[1]若映射A:(X,ρ)→(X,ρ),若对∀x,y∈X,存在0<α<1,满足不等式

ρ(Ax,Ay)≤αρ(x,y)成立．则称映射A是一个压缩映射．

Banach不动点定理[1]若(X,ρ)是一个完备的度量空间,映射A:(X,ρ)→(X,ρ)是一个压缩映射,则A在空间X上存在唯一的不动点．即,存在唯一的x′∈X满足x′=Ax′．

1 主要结论

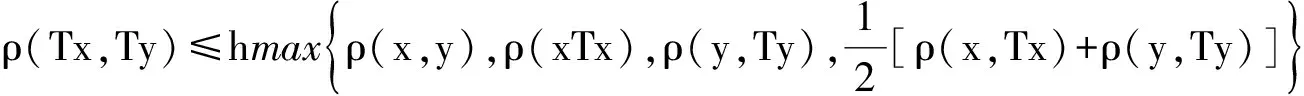
证明 任取x0∈X,定义迭代序列{xn}满足xn+1=Txn,n=0,1,2,…．则由条件知

(1)

若ρ(xn-1,xn)<ρ(xn,xn+1),则由(1)式有ρ(xn,xn+1)≤hρ(xn,xn+1),矛盾!

故有ρ(xn-1,xn)>ρ(xn,xn+1),并代入(1)式,得

ρ(xn,xn+1)≤hρ(xn-1,xn)<ρ(xn-1,xn)

(2)

知数列{ρ(xn,xn+1)}单调递减．进而得

ρ(xn,xn+1)≤hρ(xn-1,xn)≤…≤hnρ(x0,x1)

(3)

现证{xn}是X中的Cauchy列．事实上,对任意的正整数m,n,

0≤ρ(xm+n,xn)≤ρ(xm+n,xm+n-1)+ρ(xm+n-1,xm+n-2)+…+ρ(xn,xn+1)≤

即{xn}是X中的Cauchy列．由(X,d)的完备性知,设xn→x′∈X．

ρ(Tx′,x′) ≤ρ(Tx′,xn+1)+ρ(xn+1,x′)≤

事实上,假设x″是T在X中不同于x′的不动点,则

ρ(x′,x″)=ρ(Tx′,Tx″)≤hρ(x′,x″),故由0

最后,考虑误差估计

得证．

证明 任取x0∈X,定义迭代序列{xn}满足xn+1=Txn,n=0,1,2,…．则由条件知

ρ(xn,xn+1)=ρ(Txn-1,Txn)≤a(xn-1,xn)ρ(xn-1,xn)+b(xn-1,xn)ρ(xn-1,xn)+

c(xn-1,xn)ρ(xn,xn+1)+s(xn-1,xn){ρ(xn-1,xn+1)+ρ(xn,xn)}

(4)

进而有

[1-c(xn-1,xn)-s(xn-1,xn)]ρ(xn,xn+1)≤[a(xn-1,xn)+b(xn-1,xn)+s(xn-1,xn)]ρ(xn-1,xn)

(5)

则由(5)式得

(6)

现证数列{ρ(xn,xn+1)}单调递减．

事实上,若ρ(xn,xn+1)>ρ(xn-1,xn),结合(6)式及条件中二元函数a,b,c,s与数λ的关系知

(7)

矛盾．即,ρ(xn,xn+1)<ρ(xn-1,xn)(n=0,1,…)．且满足

ρ(xn,xn+1) =ρ(Txn-1,Txn)≤a(xn-1,xn)ρ(xn-1,xn)+b(xn-1,xn)ρ(xn-1,xn)

+c(xn-1,xn)ρ(xn,xn+1)+s(xn-1,xn){ρ(xn-1,xn)+ρ(xn,xn+1)}

≤[a(xn-1,xn)+b(xn-1,xn)+c(xn-1,xn)+2s(xn-1,xn)]ρ(xn-1,xn)

≤λρ(xn-1,xn)

所以由定理1的证明过程知,推论显然成立．