基于密度权值平均变化率的CFSFDP聚类算法
2018-12-06董炎焱
董炎焱
(晋中师范高等专科学校 数理科学系,山西 晋中 030600)
0 引言
聚类分析可以对数据集不进行训练而划分簇,簇内的数据相似特征明显,不同簇的数据存在差异性.实际应用中对聚类算法不断的优化,使其能够处理不同的数据类型,具有可伸缩性,适应任意簇形状,排除噪声干扰,适应高维数据等.
自从DBSCAN算法结合密度后,密度的概念逐渐被强化,CFSFDP算法适应于对任意簇形状的聚类,文献[1]计算最佳局部密度,并设置距离阈值,文献[2]对于低密度的簇进行单独聚类等等,许多研究围绕密度从细节优化CFSFDP算法,以解决人为设置截断距离dc和肉眼观察决策图以挑选聚类中心所带来的偏差.
1 CFSFDP聚类算法
1.1 传统的CFSFDP算法
CFSFDP算法存在假设条件:聚类中心必是局部密度最高的点且一个簇对应一个聚类中心,各簇之间的边界保持清晰.
设有数据点集{D},定义每个点Di的参数如下:
局部密度ρ,ρ=∑P(dij-dc);其中dij为两点的欧式距离,dc为人为设定的截断距离;当dij-dc≥0时,不计数,dij-dc0时,计数是1,即该点与其他点的距离大于等于截断距离时不考虑,否则P(dij-dc)=1,求和以得到该点的局部密度ρ.

CFSFDP算法如下:
1) 计算数据点集{D}的距离矩阵;
2) 根据局部密度ρ的定义求各数据点的ρ;
3) 根据距离δ的定义求各数据点的δ;
4) 根据ρ和δ画出决策图,通过观察找到聚类中心{w1,w2…wi};
动脉导管开放是早产儿常见疾病,目前早产儿PDA的自然发展过程仍未完全明确,PDA发生的部分高危因素仍存在争议,对PDA是否进行药物、手术干预,何时进行药物、手术干预仍存在争议。尽管已经有大量证据证实动脉导管持续开放可能有害,但是目前尚缺乏关闭PDA治疗方案的远期益处或害处的相关证据。尽管产前激素、肺泡表面活性物质及非创伤性呼吸支持已经得到广泛应用,目前尚无评估动脉导管持续开放对早产儿死亡率及并发症影响的临床试验,近年来关于PDA治疗的研究最大的改变是减少PDA的治疗[3]。

1.2 CFSFDP算法的决策图
以局部密度ρ为横坐标,距离δ为纵坐标,画出决策图.如图1所示.

图1 CFSFDP决策图
由图1可以看出在决策图的右上角存在密度峰值点,通常把这些点称为聚类中心,它们的ρ值最大,δ较高.理论上可以通过观察找到聚类中心.
1.3 CFSFDP算法的局限性
ρδ的决策图较为直观,如果根据图1选择聚类中心,会发现只有一个密度峰值点.但由数据表发现ρ1=8,δ1=13.243 513 23;ρ2=8,δ2=13.289 747 16,存在两个密度峰值点,这两个点在图中基本重合在一起,人工选择就会出现漏选.因此单纯地以决策图来确定聚类中心存在不确定性,影响算法的准确性.
2 基于密度权值平均变化率的CFSFDP算法
2.1 算法原理
根据原算法对ρ和δ的定义,如果ρ是最大,那么它是密度峰值点,取的是与密度峰值点最远的距离作为δ;如果是非密度峰值点,从比该点更高的ρ的范围内选取与该点最近的距离作为δ,也就是说密度峰值点的都ρ和δ较大,分布在决策图的右上角.针对聚类中心点重叠而人工不能分辨的问题,本文提出基于密度权值平均变化率的CFSFDP算法.
区分点最直接的方法是增加点的差异性,因此采用的ρ和δ乘积作为密度权值.为了能够通过计算得到聚类中心,将权值继续变化,引入权值差,实际为线段的斜率,也称为平均变化率,反应偏离的变化趋势.
基于密度权值平均变化率的CFSFDP算法如下:
1) 根据传统的CFSFDP算法求出ρ和δ;
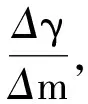
3) 搜索拐点,在权值差图从左向右遍历,设拐点为x,满足x=argmax|Δγi+1-Δγi|;
4) 拐点x左边的点(包括x)均为聚类中心;
5) 根据原算法的5)完成其余非聚类中心数据点的归类.
3 实验
实验数据来源http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/indexch.htm,没有噪声数据,去除了数据标签,并取对数.
根据改进算法的2)画出权值图,如图2.
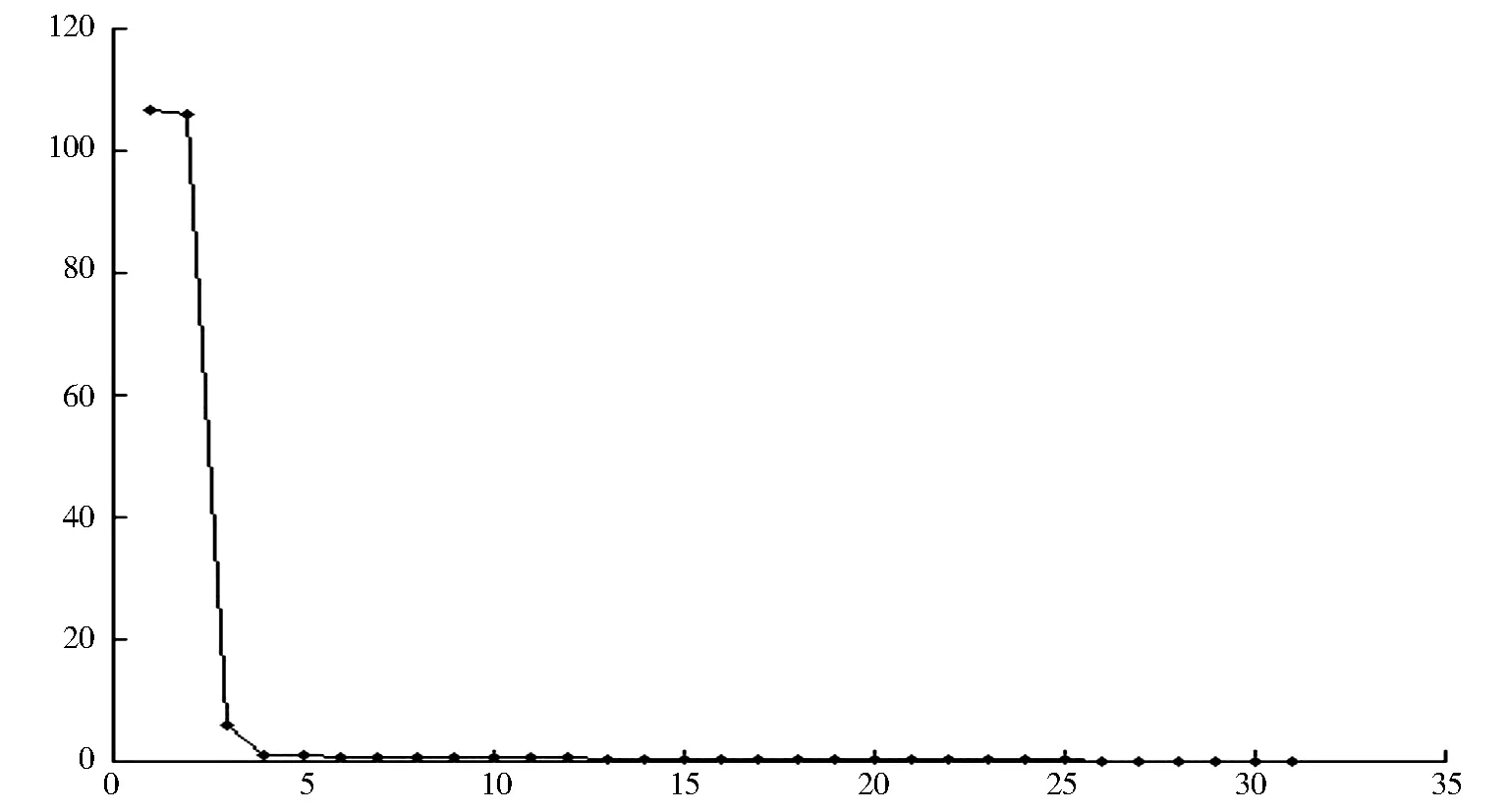
图2 权值图
可以看出密度权值表现为下降趋势,呈现为“先急后缓”,从左向右遍历时极值点出现在左边的几率较大.计算权值的平均变化率,也是线段的斜率,得到图3权值差图.
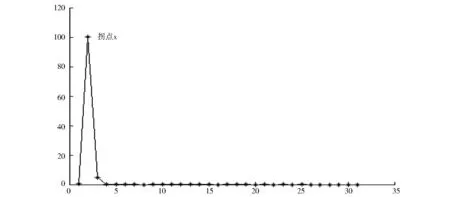
图3 权值差图
权值差图中可以看出拐点的位置,但是考虑到截断距离dc的人为选取影响拐点的位置,所以计算平均变化率以求得准确的拐点.计算结果见表1.

表1 密度权值平均变化率
表1中选取前30个数值,极大值出现的位置为100.312 7,对应于图3的拐点x,因此选择x左边的点包括x,产生2个聚类中心,将基本重叠的聚类中心有效地分开.原算法由图1的决策图只能看到一个聚类中心.
4 结论
改进的CFSFDP聚类算法原则上解决了决策图中聚类中心重叠而造成漏选的问题,以计算密度权值的平均变化率得到拐点,从而产生聚类中心,去除了人为的因素,客观地反应了聚类中心的存在个数.不足之处在于没有判断选出邻近的聚类中心是否需要合并.
