构建解题思维模型突破化学计算难点

2018-12-06广东刘汉国

教学考试(高考化学) 2018年5期

广东刘汉国

纵观近五年高考试题不难发现，计算题大约占10分左右。高考化学计算题以解决实际问题为背景，以实验题、工业流程题、化学反应原理题等为题型，以图象、图表、文字等为信息呈现形式，融合学科间的知识及数学模型，考查学生提取信息的能力、分析问题的能力、计算能力并且从中渗透证据推理与模型认知等核心素养。

一、发现问题

从高考试卷抽样分析中不难发现计算题的得分不高，其主要原因是学生缺乏解题思维和方法技巧。老师为了让学生考高分而盲目地开展“题海战术”,只关注学生的做题数量而不注重对学生学习能力的培养,从而导致学生“一听就懂,一做就错”的现象仍屡见不鲜。本文针对不同类型的计算题，通过构建不同类型的解题思维模型将其逐一突破。所谓解题思维模型，是对于某一类问题而言，如果能把握问题的相关因素和特定关系，然后对问题进行综合分析，最终对该问题进行问题建模。本文构建了关系式法思维模型、方程组法思维模型、比例法思维模型和极限法思维模型四种解题思维模型，以供同仁们在教学时参考借鉴。

二、解题思维模型的构建与应用

1. 关系式法思维模型

关系式法是根据方程式系数、反应前后的原子守恒、得失电子守恒等，寻找各反应物与生成物之间存在的最基本的比例(数量)关系，构建的关系式法思维模型如图1所示。

图1 关系式法思维模型

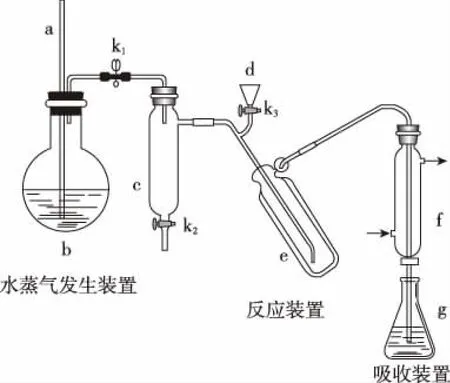
(5)取某甘氨酸(C2H5NO2)样品m克进行测定，滴定g中吸收液时消耗浓度为cmol·L-1的盐酸VmL，则样品中氮的质量分数为 %，样品的纯度≤ %。

【总结】该题目中涉及三个反应：C2H5NO2生成NH3的反应、NH3与H3BO3的反应、NH3·H3BO3与HCl的反应，三个反应都是前者的生成物是后者的反应物，我们称之为连续反应。对于连续反应的相关计算，无需关注反应的过程，只需找到已知量与未知量的关系，带入数据即可。

2.方程组法思维模型

依据题设条件设立未知数，根据题目中所给的已知物理量以及方程式系数、原子守恒等比例关系，列方程组求解，具体的思维模型如图2所示。

图2 方程组法思维模型

例2(2017北京，27卷节选)SCR和NSR技术可有效降低柴油发动机在空气过量条件下的NOx排放。

(1)SCR(选择性催化还原)工作原理：

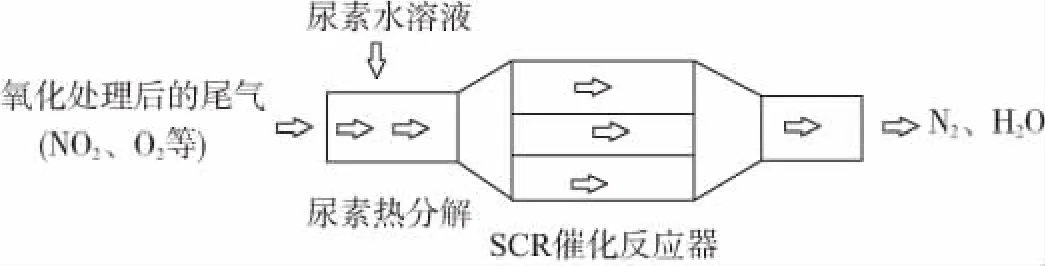
①尿素[CO(NH2)2]水溶液热分解为NH3和CO2，该反应的化学方程式：__________。

④尿素溶液浓度影响NO2的转化，测定溶液中尿素(M=60 g·mol-1)含量的方法如下：取ag尿素溶液，将所含氮完全转化为NH3，所得NH3用过量的v1mLc1mol·L-1H2SO4溶液吸收完全，剩余H2SO4用v2mLc2mol·L-1NaOH溶液恰好中和，则尿素溶液中溶质的质量分数是_____________。

CO(NH2)2～ 2NH3～ H2SO4

xmolxmol

2NaOH ～ H2SO4

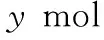
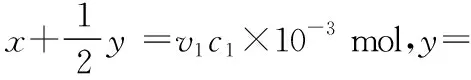
【总结】该题目中涉及三个反应：CO(NH2)2生成NH3的反应、NH3与H2SO4的反应、NaOH与 H2SO4的反应，其中后两个反应为独立反应。对于发生多个独立反应的相关计算，应用方程组法思维模型比较简单。此外，对于有多个未知量的相关计算，一般都可以应用方程组法思维模型。

3.比例法思维模型

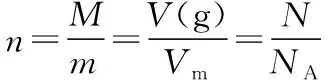
图3 比例法思维模型

例3．(2017江苏卷，18节选)碱式氯化铜是重要的无机杀菌剂。

【解析】由实验②可以求出该样品中所含Cl-的物质的量，由氯离子守恒得：

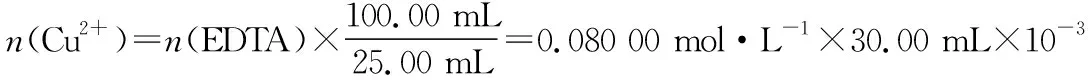
再由化合物中电荷守恒得：n(OH-)=2n(Cu2+)-n(Cl-)=2×9.600×10-3mol-4.800×10-3mol=1.440×10-2mol，分别求出这3种离子的质量，根据质量守恒，求出H2O的质量：

m(Cl-)=4.800×10-3mol×35.5 g· mol-1=0.170 4 g。

m(Cu2+)=9.600×10-3mol×64 g· mol-1=0.614 4 g。

m(OH-)=1.440×10-2mol×17 g· mol-1=0.244 8 g。

【总结】对于化学式、比值等相关计算，可以应用比例法思维模型。

4.假设法思维模型

对于混合物的相关计算，由于多种物质参加反应，情况复杂并且条件不足时，用“假设法”，假设全部是一种物质，或只发生一种反应，或“减少”发生反应的物质，使计算简单化，具体的思维模型如图4所示。

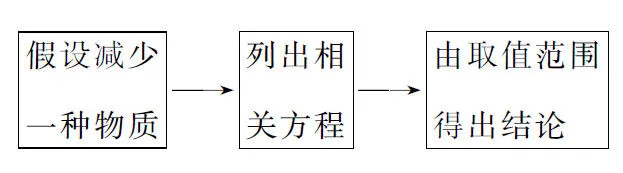
图4 假设法思维模型

例4．已知：Fe5O7可以看作Fe2O3和Fe3O4的混合物。现有Fe、Fe2O3、Fe5O7混合物共0.1 mol，加盐酸后固体全部溶解，共收集到0.01 mol H2，且向反应后的溶液中加入KSCN溶液不显红色，则原混合物中铁的物质的量为

( )

A.0.05 mol B.0.06 mol

C.0.07 mol D.0.08 mol

【解析】本题有三种反应物且全部溶解于盐酸，但是反应后生成的Fe3+还与Fe进行反应。该题目反应比较复杂，Fe、Fe2O3、Fe5O7三种物质的量均未知，而题中只有两个已知量，故依据极值法计算判断。

加盐酸后固体全部溶解，共收集到0.01 mol H2，得到与盐酸反应生成氢气的铁物质的量为0.01 mol。反应后的溶液中加入KSCN溶液不显红色说明不含铁离子，溶液中全部为亚铁离子，故我们提出两种极端假设：假设混合物 0.1 mol为Fe、Fe2O3和假设混合物0.1 mol为Fe、Fe5O7。在两种假设的前提下进行计算，解得铁的物质的量为0.055

【总结】极端假设法在判断混合物的组分、生成物的含量、平衡体系组分的浓度等有比较多的应用。极端假设法可以把一些抽象的、复杂的问题具体化、简单化，使计算简便、快捷，是一种行之有效的好方法。