基于不同判别准则的硬岩矿柱状态识别模型
2018-12-06赵国彦刘建周健
赵国彦,刘建,周健
基于不同判别准则的硬岩矿柱状态识别模型
赵国彦,刘建,周健
(中南大学资源与安全工程学院,湖南 长沙,410083)
基于162个硬岩矿柱样本,构建不同判别准则下矿柱状态识别的Fisher判别分析(FDA)模型、距离判别分析(DDA) 模型和Bayes判别分析(BDA)模型,进而与多元逻辑回归(MLR)、极限学习机(ELM)、最小二乘支持向量机(LS-SVM)、支持向量机(SVM)、高斯过程分类(GPC)、分类回归树(CART)、神经网络(ANN)共7种常用的统计学习方法进行比较,同时探讨主成分分析(PCA)方法提高识别准确率的可行性,并对矿柱状态影响因子进行敏感性分析。研究结果表明:这10种统计学习方法中,GPC的准确率最高,FDA的准确率次之,然后是MLR,CART的准确率最低;对于3种判别分析方法,FDA的准确率最高,DDA与BDA的准确率几乎相当;增加判别指标,DDA和BDA的判别准确率显著降低,其他方法对判别指标增减不敏感;对某些方法,原始数据经PCA处理后不能提高其判别准确率;矿柱状态对矿柱应力最敏感,其次是矿岩单轴抗压强度,其对矿柱宽高比的敏感性较低。
硬岩矿柱;状态识别;判别分析;主成分分析;敏感性分析
矿柱是地下矿山支撑顶板围岩、维持采场稳定的关键结构要素,矿柱失稳将导致空区顶板大面积坍塌,造成大量的人员伤亡和严重的财产损失,因此,对矿柱稳定性进行研究,对实现地下矿山高效、安全回采具有重要意义。目前,矿柱稳定性分析的研究方法主要有安全系数法、数值模拟法、可靠性分析法和统计学习理论[1]。由于岩体结构的不均质性和复杂性,自SALAMON等[2]利用极大似然法提出煤柱强度的经验公式以来,基于历史数据(稳定与破坏的矿柱实例)的反分析方法一直是人们研究矿柱的重要手段,HEDLEY等[3]基于硬岩矿柱实例样本提出了计算矿柱强度的经验公式。近年来,美国NIOSH机构开发的地下石灰矿山矿柱设计软件S-Pillar与地下煤矿煤柱设计软件ALPS和ARMPS都是基于大量实际数据开发的[4]。本质上,统计学习理论也是一种基于历史数据的反分析方法。MONJEZI等[5]利用神经网络算法(ANN)预测矿柱应力并进行矿柱设计。GHASEMI等[6]运用模糊逻辑理论预测煤柱尺寸。WATTIMENA[7]基于178个硬岩矿柱实例,利用多项逻辑回归模型(MLR)预测硬岩矿柱的稳定性。余佩佩等[1]利用数量化理论研究地下矿山矿柱的稳定性。ZHOU等[8]利用线性判别分析(LDA)和支持向量机(SVM)预测矿柱稳定性。尽管统计学习理论可解释性不强,无法反映问题的本质,然而,其作为一种分析方法对指导工程实践仍具有重要意义。多元判别分析概念明确,理论简单,无初始参数,与其他方法相比具有一定的可解释性,且便于工程应用。为此,本文作者将多元判别分析理论引入到矿柱状态识别中,重点比较不同判别准则下距离判别分析(DDA)、贝叶斯判别分析(BDA)和Fisher判别分析(FDA)的优劣,同时与MLR、极限学习机(ELM)、最小二乘支持向量机(LS-SVM)、支持向量机(SVM)、高斯过程分类(GPC)、分类回归树(CART)和ANN这7种常用的统计学习方法进行比较(利用网格算法和交叉验证方法确定最佳初始参数,并循环预测200次);此外,考察原始数据经主成分分析(PCA)处理后各种方法判别准确率的变化情况,并基于FDA和MLR对矿柱稳定性影响因素进行敏感性分析。
1 多元判别分析原理



式中:()为判别函数。
距离判别准则的基本思想为:按待判样本与已知总体的马氏距离确定判别函数


贝叶斯判别准则的基本思想为:按平均误判损失最小确定判别函数
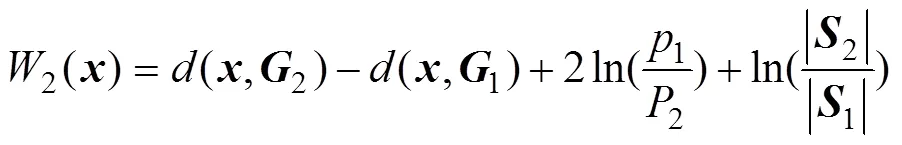
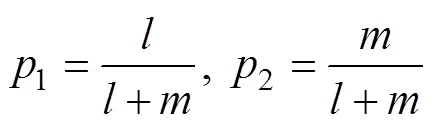
Fisher判别准则的基本思想为:按类内散度足够小,类间散度足够大确定判别函数

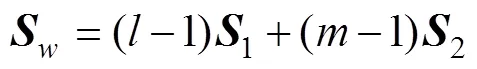

值得注意的是:在应用贝叶斯判别准则时,需假定已知总体G服从正态分布,而距离判别准则和Fisher判别准则对已知总体分布无任何要求。
2 工程实例
2.1 矿柱破坏形式
矿柱对采矿所引起荷载的整体响应取决于该矿柱的绝对或相对大小、矿柱岩体的地质构造和围岩对矿柱所施加的表面约束特性。大多数矿柱破坏的主要形式是矿柱表面的剥落、剪切破坏和与软弱夹层、节理等构造有关的破坏类型[10],如图1所示。
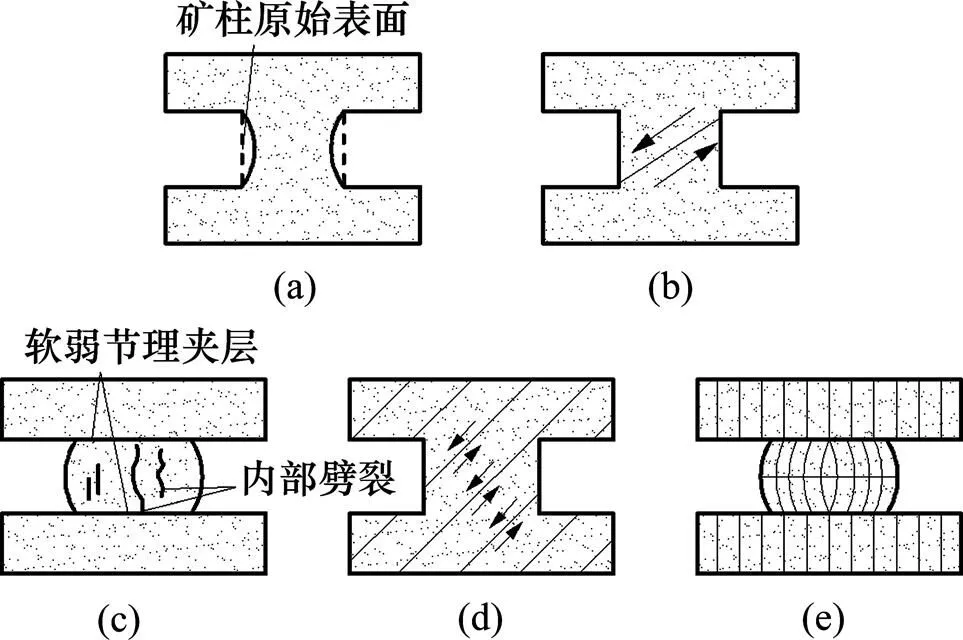
(a) 矿柱表面的剥落、板裂破坏;(b) 低宽高比矿柱的剪切破坏;(c) 由软弱夹层引起的矿柱内部劈裂破坏;(d) 沿地质结构面的滑移破坏;(e) 沿地质结构面的溃曲破坏
2.2 确定判别因子并构造样本集
WATTIMENA[7]采用矿柱宽高比、矿岩单轴抗压强度、矿柱应力共3种判别因子,余佩佩等[1,8]采用矿柱宽度、矿柱高度、矿柱宽高比、矿岩单轴抗压强度、矿柱应力共5种判别因子,ZHOU等[11]采用矿柱宽度、矿柱高度、矿柱宽高比、矿岩单轴抗压强度、矿柱应力、矿柱强度共6种判别因子预测矿柱稳定性。目前,几乎所有硬岩矿柱强度经验公式均包括矿柱宽度、矿柱高度(或矿柱宽高比)和矿岩单轴抗压强度[3]。为考虑不规则硬岩矿柱的强度,LUNDER等[12]定义了矿柱约束(pillar confinement,即矿柱中心平均最小主应力与平均最大主应力之比)以代替矿柱宽高比,同时其也反映了矿柱中心的受力状态。基于上述研究,本文以矿柱宽度、矿柱高度、矿柱宽高比、矿柱约束、矿岩单轴抗压强度、矿柱应力、矿柱强度作为判别因子。图2所示为基于本文数据采用互信息(mutual information)方法计算的每个判别因子对实测结果的相关性,计算所得互信息值()越大,则表明该判别因子对实测结果的作用越强。判别因子互信息值见图2。由图2可知:7个判别因子对矿柱状态的影响程度大体相当,无冗余判别因子。

图2 判别因子互信息值M
本文以162个完整硬岩矿柱样本为例进行建模,所有数据取自文献[12](文献[12]中共有178例样本,本文去除其中16例判别指标不全的样本)。所有矿柱及其顶底板围岩的岩体质量分级值RMR为60~85,岩体质量等级为Ⅰ~Ⅱ级(RMR分级),不包含结构面,矿柱破坏模式以图1(a)和(b)所示2种类型为主。矿柱高度沿最大主应力方向确定;矿柱宽度垂直于矿柱高度,针对矩形矿柱,矿柱宽度为矩形最小边长;矿柱应力采用面积承载理论或数值模拟法确定;矿柱强度采用LUNDER[12]的矿柱强度经验公式确定。LUNDER[12]采用通用的分级方法将上述矿柱分为稳定、不稳定、破坏3级,数量分别为58,37和67个,考虑到硬岩矿柱的渐进破坏特性,不稳定矿柱最终有可能破坏失稳,故本文将不稳定矿柱归为破坏一类。全体矿柱样本的统计特性见表1。图3所示为全体矿柱样本散点图矩阵,该矩阵右上角代表判别因子间的相关系数,对角线代表判别因子的分布特征,左下角代表对应判别因子间的关系。
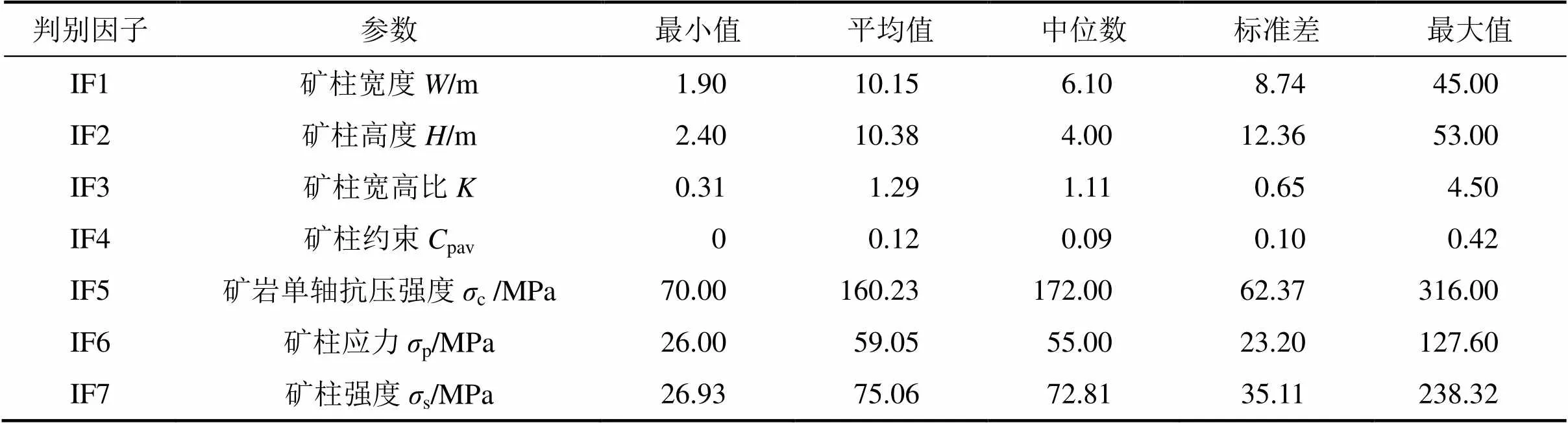
表1 硬岩矿柱样本统计特性
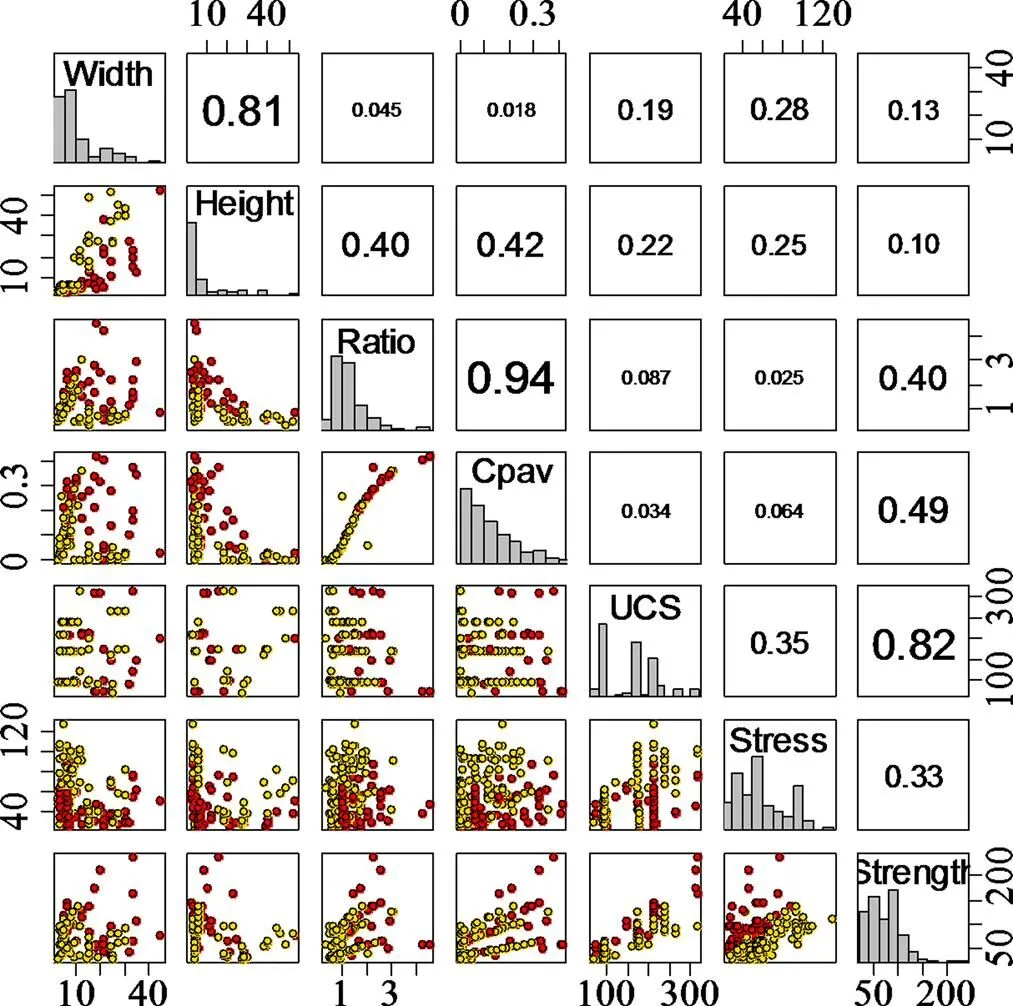
图3 矿柱样本散点图矩阵
2.3 构建多元判别模型
为综合比较多元判别分析及另外7种统计学习方法在硬岩矿柱状态识别中的性能,参照余佩佩 等[1, 7−8,11]采用的判别指标,本文根据不同的判别因子组合构建了A,B,C和D共 4种判别模型(见表2)。为了对原始样本数据进行处理,剔除冗余信息,钱兆明等[13]提出了基于PCA-FDA的岩体质量等级分类模型,宫凤强等[14]提出了砂土液化预测的PCA-DDA模型,他们采用主成分判别指标进行后续建模,以提高模型准确率。为此,本文对模型D进行主成分分析,分别以4个和5个主成分指标(主成分累计贡献率一般为85%~95%[14])构建模型E和模型F,以此探讨主成分分析方法提高识别准确率的可行性。因此,本文共构建6种判别模型,如表2所示。针对每种判别模型,以上述10种统计学习方法进行建模。
首先对原始数据进行归一化处理,使所有判别因子属于[0,1];然后,随机抽取80%作为训练样本,其余20%作为测试样本。对于模型E和模型F,经数据归一化后还进行主成分分析(PCA),提取主成分指标。模型ELM和ANN初始参数为隐含层神经元个数,LS−SVM和SVM初始参数为规则化参数和核函数参数2。针对模型ELM,LS-SVM和SVM,采用网格算法和10次10折交叉验证确定最佳初始参数。由于ANN模型(单隐层BP网络)训练时间较长,为节省时间,采用1次10折交叉验证(ANN模型运行200次需耗时47 h);FDA,DDA,BDA,MLR和CART无需初始参数,而GPC可进行超参数自适应获取。模型训练完毕后,用测试样本进行检验,获得测试样本预测准确率。上述过程重复200次,求取平均预测准确率,以保证结果的可靠性和代表性,计算流程如图4所示。
上述运算在MATLAB环境中完成,FDA,DDA和BDA程序自行编制,MLR,CART和ANN采用MATLAB自带函数,ELM程序采用HUANG[15]编写的程序,LS-SVM程序采用LS-SVMlab1.8[16]工具箱编写,SVM程序采用LIBSVM3.11[17]工具箱编写,GPC程序采用GPML4.0[18]工具箱编写。按照计算流程将上述程序编写到一个M文件中,运行结果见表3。图5所示为每种模型下10种统计学习方法测试样本预测准确率的箱线图。
从表3可知:GPC在10种统计学习方法中准确度最高,其次是FDA,然后是MLR,其平均测试准确率分别为0.904 5,0.904 3和0. 900 3;CART准确率最低,其平均准确率只有0.830 9,DDA和BDA的准确率相当,且同时比SVM和ELM的准确率低。表3中同时以不同标记标出了每种判别模型下测试准确率最高的3种统计学习方法,其中,*表示最大值,**表示次大值,***表示第3大值;GPC在模型C,D,E和F中取得最大准确率,FDA和MLR分别在模型A和B中取得最大准确率,这也反映出GPC,FDA和MLR与其他统计学习方法相比具有优越性。

表2 判别模型
注:X表示主成分;括号内数值为累计贡献率。
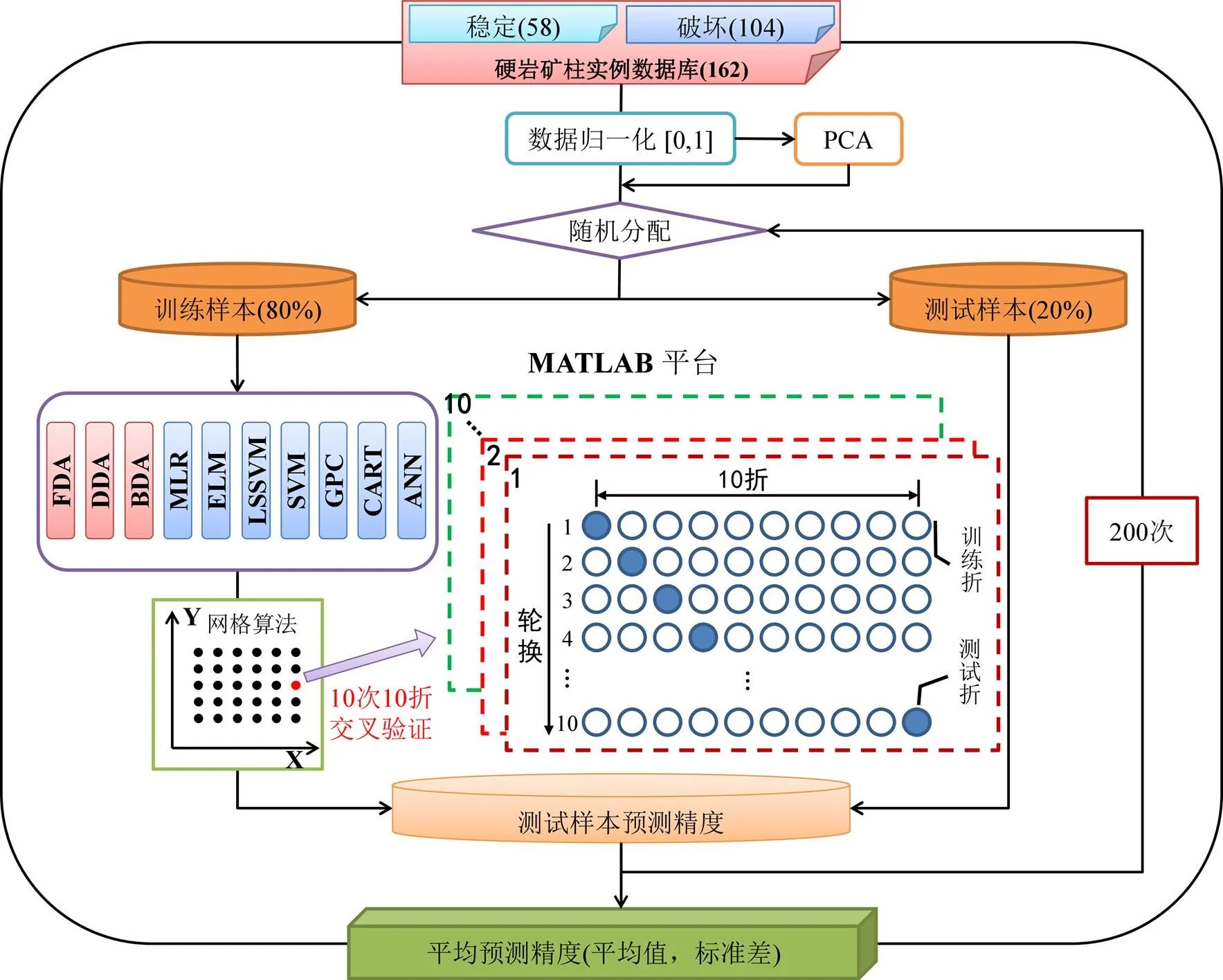
图4 计算流程

表3 测试结果
注:*表示最大值,**表示次大值,***表示第3大值;括号内数据为标准差。
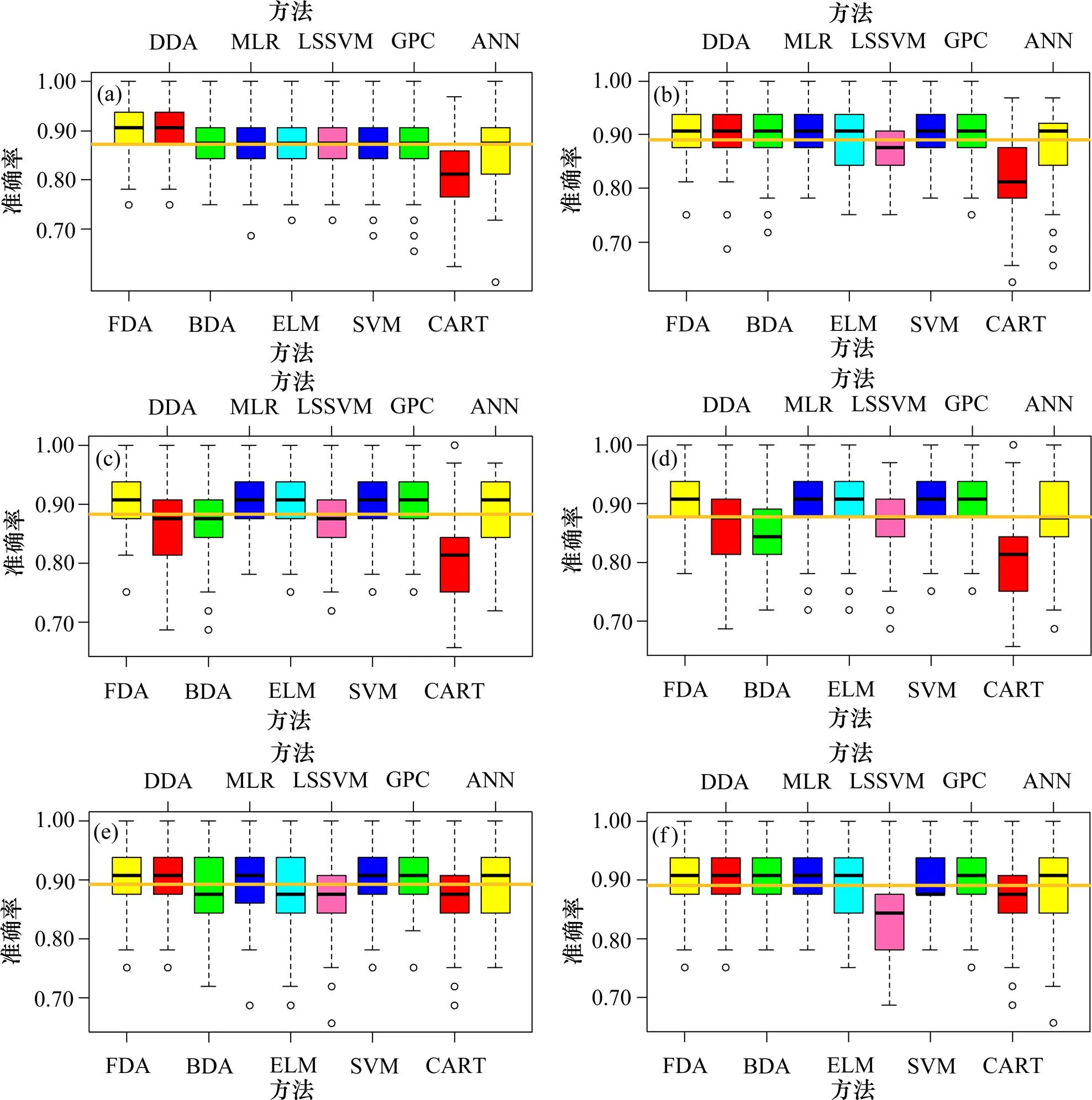
(a) 模型A;(b) 模型B;(c) 模型C;(d) 模型D;(e) 模型E;(f) 模型F
以每种模型的平均测试准确率来看,模型E取得最大值,模型F次之,然后是模型B,其平均准确率分别为0.891 2,0.890 8和0.889 9。经PCA处理后,模型E和F与模型D相比,其测试准确率有一定提高,但这仅仅是10种统计学习方法的平均结果。需要注意的是:CART,DDA和BDA的准确率提高最显著,而LS-SVM准确率有明显降低,其他方法的准确率则无明显变化。应用PCA降低数据特征冗余,一方面消除判别指标间的相关性(主成分指标相关系数为0),另一方面剔除低贡献率的主成分指标,从而提炼数据(主成分指标累计贡献率一般保留85%~ 95%[14])。然而,以上结果表明,对某些方法如LS-SVM,采用PCA处理后的数据并不能提高其测试准确率;同时,尽管DDA,BDA和CART准确率提高显著,但仅仅是与自身相比,其测试准确率不一定比其他方法的高。此外,从模型A,B,C和D来看,增加判别指标,DDA和BDA的测试准确率显著降低,而其他方法对判别指标不敏感。
以模型D为例,10种统计学习方法测试准确率的累计分布曲线(CDF)见图6。其中,图6(b)为图6(a)的局部放大图。累计分布曲线越低,表明该方法越好。从图6(b)可看出:GPC,FDA和MLR明显优于ELM,ANN,LS-SVM,BDA,DDA和CART;GPC和FDA优于MLR和SVM,而MLR与SVM的性能几乎相当。就3种判别分析方法来说,明显FDA最好,其次是BDA,最后是DDA。
2.4 判别因子敏感性分析
基于FDA和MLR,运用傅里叶振幅灵敏度分析方法(Fourier amplitude sensitivity test, FAST)对模型D进行灵敏度分析,以探讨矿柱状态对上述判别指标的敏感性。应用FAST可以计算出影响模型输出值的各参数的一阶灵敏度指数(),其反映仅由1个参数的变异对模型输出值的变异所作出的贡献。采用FRANCESCA等[19]开发的SAFE工具箱进行FAST分析,分析结果见图7,其中,图7(a)所示为基于FDA的分析结果,图7(b)所示为基于MLR的分析结果。
从图7(a)和(b)可知:矿柱状态对矿柱应力最敏感,这与ZHOU等[11]的研究结果相同;其次是矿岩单轴抗压强度。然而,矿柱状态对矿柱宽高比的敏感性较低,但对矿柱宽度和矿柱高度的敏感性较高,这反映出在矿柱强度经验公式中,以矿柱宽度和矿柱高度作为未知参量比单一未知参量矿柱宽高比更好。事实上,HEDLEY等[3]建立的硬岩矿柱强度经验公式就是以矿柱宽度和矿柱高度作为未知参量,而没有采用单一的矿柱宽高比,LUNDER[12]则采用矿柱约束作为未知参量。在分析结果中,仅仅矿柱状态对矿柱强度的敏感性有较大差别,这可能与FDA和MLR的理论差异有关,其余判别因子对矿柱状态的敏感性相同。

(a) 准确率累计;(b) 图6(a)的局部放大图

(a) 基于FDA的分析结果;(b) 基于MLR的分析结果
3 结论
1) 10种统计学习方法中,GPC准确率最高,FDA次之,然后是MLR,CART准确率最低。就3种判别分析方法来说,FDA最好,DDA与BDA的性能几乎相当。由于FDA概念明确,理论简单、无初始参数,所以首先推荐采用。
2) 增加判别指标,DDA和BDA的判别准确率显著降低,而其他方法对判别指标不敏感。采用主成分判别指标(原始数据经PCA处理),CART,DDA和BDA的判别准确率提高显著,而LS-SVM的判别准确率明显降低,其他方法的判别准确率无明显变化。所以,对某些方法,采用PCA处理后的数据并不能提高其判别准确率。
3) 矿柱状态对矿柱应力最敏感,对矿岩单轴抗压强度的敏感性次之,对矿柱宽高比的敏感性较低。
[1] 余佩佩, 赵国彦, 周礼. 基于数量化理论Ⅱ的地下矿山矿柱稳定性判别[J]. 安全与环境学报, 2014, 14(5): 45−49. YU Peipei, ZHAO Guoyan, ZHOU Li. Pillars’ stability assessment in the underground mines based on the quantification theory Ⅱ[J]. Journal of Safety and Environment, 2014, 14(5): 45−49.
[2] SALAMON M D G, MUNRO A H. A study of the strength of coal pillars[J]. Journal of the south African Institute of Mining and Metallurgy, 1967, 68: 55−67.
[3] HEDLEY D G F, GRANT F. Stope-and-pillar design for the Elliot Lake Uranium Mines[J]. Canadian Mining and Metallurgical Bulletin, 1972, 65: 37−44.
[4] ESTERHUIZEN G S, DOLINAR D R, ELLENBERGER J L. Pillar strength in underground stone mines in the United States[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(1): 42−50.
[5] MONJEZI M, SEYED M H, MANOJ K. Superiority of neural networks for pillar stress prediction in bord and pillar method[J]. Arabian Journal of Geosciences, 2011, 4(5): 845−853.
[6] GHASEMI E, ATAEI M, SHAHRIAR K. An intelligent approach to predict pillar sizing in designing room and pillar coal mines[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 65(75): 86−95.
[7] WATTIMENA R K. Predicting the stability of hard rock pillars using multinomial logistic regression[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 71(80): 33−40.
[8] ZHOU Jian, LI Xibing, SHI Xiuzhi, et al. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2734−2743.
[9] 薛毅, 陈立萍. 统计建模与R软件[M]. 北京: 清华大学出版社, 2007: 442−443. XUE Yi, CHEN Liping. Statistical modeling and R software[M]. Beijing: Tsinghua University Press, 2007: 442−443.
[10] 李坚玲. 全面法采场矿柱稳定性及影响因素敏感性分析[J]. 有色金属(矿山部分), 2010, 62(5): 6−8. LI Jianling. Stope pillar stability and sensitivity analysis of effect factors in overall mining method[J]. Nonferrous Metals(Mining Section), 2010, 62(5): 6−8.
[11] ZHOU Jian, LI Xibing, MITRI H S. Comparative performance of six supervised learning methods for the development of models of hard rock pillar stability prediction[J]. Natural Hazards, 2015, 79(1): 291−316.
[12] LUNDER P J. Hard rock pillar strength estimation an applied empirical approach[D]. Vancouver: The University of British Columbia, 1994: 46−130.
[13] 钱兆明, 任高峰, 褚夫蛟, 等. 基于PCA法和Fisher判别分析法的岩体质量等级分类[J]. 岩土力学, 2016, 37(增刊2): 427−432. QIAN Zhaoming, REN Gaofeng, CHU Fujiao, et al. Rock mass quality classification based on PCA and Fisher discrimination analysis[J]. Rock and Soil Mechanics, 2016, 37(Suppl 2): 427−432.
[14] 宫凤强, 李嘉维. 基于PCA-DDA原理的砂土液化预测模型及应用[J]. 岩土力学, 2016, 37(增刊1): 448−454. GONG Fengqiang, LI Jiawei. Discrimination model of sandy soil liquefaction based on PCA-DDA principle and its application[J]. Rock and Soil Mechanics, 2016, 37(Suppl 1): 448−454.
[15] HUANG Guangbin. What are extreme learning machines? Filling the gap between Frank Rosenblatt’s dream and John von Neumann’s Puzzle[J]. Cognitive Computation, 2015, 7(3): 263−278.
[16] BRABANTER K, KARSMAKER P, OJEDA F, et al. LS-SVMlab toolbox user's guide(version 1.8)[EB/OL]. [2016−12−8]. http://www.esat.kuleuven. be/ sista/ lssvmlab/.
[17] HSU C W, CHANG C C, LIN C J. A practical guide to support vector classification[EB/OL]. [2017−02−20]. https://www.csie. ntu.edu.tw/~cjlin/libsvm/index.html.
[18] RASMUSSEN C E, NICKISCH H. The GPML toolbox version 4.0[EB/OL]. [2017−01−12]. http://www.gaussianprocess.org/ gpml/code/matlab/doc/manual.pdf.
[19] FRANCESCA P, FANNY S, THORSTEN W. A Matlab toolbox for global sensitivity analysis[J]. Environmental Modelling & Software, 2015, 70: 80−85.
(编辑 陈灿华)
Recognition model of hard rock pillars state based on different discriminant criterions
ZHAO Guoyan, LIU Jian, ZHOU Jian
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Based on 162 hard rock pillar cases, three discriminant models for pillar stability determination including Fisher discriminant analysis(FDA) model, distance discriminant analysis(DDA) model and Bayes discriminant analysis(BDA) model were constructed, and then they were compared with 7 statistical learning methods which were multiple logistic regression(MLR),extreme learning machines(ELM),the least squares support vector machines(LS-SVM), support vector machines(SVM), Gaussian process classification(GPC), classification and regression tree(CART) and artificial neural network(ANN). At the same time, the feasibility of increasing the recognition accuracy with principal component analysis(PCA) was discussed and sensitivity analyze of each influence factor were carried out. The results show that the best three methods are GPC, FDA and MLR, CART has the lowest accuracy, and the accuracy of DDA and BDA is nearly equal. The accuracy of DDA and BDA decreases with the increase of the number of influence factors, but accuracies of other methods are not sensitive to the change of the factor numbers. For some methods, the prediction accuracy does not increase as expected when the raw data are processed by PCA. Pillar state is most sensitive to the pillar stress, followed by the uniaxial compressive strength of the rock, and the sensitivity to the ratio of pillar width to its height is low.
hard rock pillar; state recognition; discriminant analysis; principal component analysis; sensitivity analysis
10.11817/j.issn.1672-7207.2018.11.023
TD 853
A
1672−7207(2018)11−2813−08
2017−11−02;
2018−01−23
国家自然科学基金资助项目(51374244) (Project(51374244) supported by the National Natural Science Foundation of China)
赵国彦,博士,教授,从事岩石力学与工程等研究;E-mail: gy.zhao@263.net
