给“综合与实践”生长的力量

杨琴琴

教学实录

一、谈话交流，引入课

教师出示图1，引导学生观察信封上的信息，引出邮票中的数学问题。

二、理解资费，建立模型

1.创设情境，自主探究

教师让学生帮助两个留守儿童给在外打工的爸爸妈妈寄信（两封信分别是从慈利县寄往张家界市和广东省广州市）。请学生认真研读资费表（如图2所示），试着算一算这两封信的邮费。

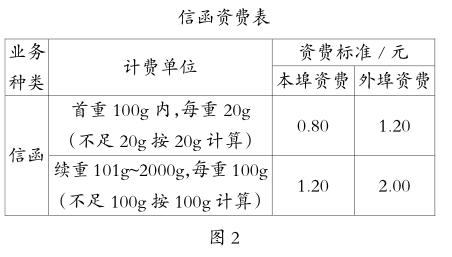
师：孩子们，你们算出来了吗？

生1：算不出来，信函的重量我们不知道。

师：经过邮局工作人员称重，第一封信重87g，第二封信重115g，现在能算出信函的邮费吗？

生2：不能，邮费还与信函寄往的目的地有关，资费表中的本埠和外埠指的是哪儿无法确定。

师：这个问题很有价值，谁能解答？

生3：本埠应该就是本地，外埠应该就是外地。

生4：本埠可能是指本县，外埠或许指外县。

生5：我觉得本埠和外埠或許就是指本市和外市。

教师指出，就我们慈利县而言，本埠是指张家界市范围之内，外埠是指张家界市之外。随后让学生计算邮费。

2.把握要领，建立模型

师：大家都算出来了吗？谁来说说你的解题思路？

生6：第一封信的质量是87g，是寄往本埠的，每20g为一个计费单位，不足20g按照20g计算，87g里包含了5个这样的计费单位，寄往本埠的收费标准是每20g收费0.80元，所以是0.8×5=4（元）。第二封信是寄往外埠的，115g超出了首重100g的范围，得分段计费：115=100+15，100÷20=5（个）。首重：1.2×5=6（元），续重：2×1=2（元），共6+2=8（元）。

三、合作探究，解决问题

1.生成问题，合作探究

师：大家算出了两封信各自需要支付的邮费，接下来请大家根据邮费分别为这两封信贴上面值80分和1.20元的邮票。（学生动手贴邮票）

师：（展示6种贴法，如图3）看到这些贴法，你有什么想说的吗？

生7：邮票数量太多，信封上很多重要信息被盖住了。

生8：我觉得可以减少邮票数量，增加邮票面值。

师：这种方案可行吗？（生：可行）其实为了解决这个问题，邮局还有一个补充规定：为方便机器检信，一封不超过100g的信函最多可贴3枚邮票，不超过400g的信函最多可贴4枚邮票。那现在我们邮寄不超过100g的信函，只用80分和1.2元的邮票，能满足需要吗？

生9：我觉得不能，刚刚求出87g的信需要4元，而3张1.2元的邮票最大也只能组合出3.6元。

师：说得真好！不过，单凭一封87g的信说明不了问题，我们得想办法验证。怎么验证？

生10：先把100g以内信函的所有资费算出来，再用80分和1.2元的邮票进行组合，就知道是否满足所有需要了。

师：行，就按这位同学说的去做，开始行动吧！（学生小组活动）

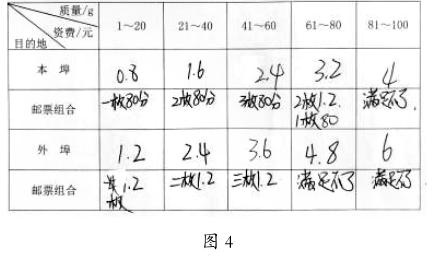
师：（出示图4）只用这两种面值，最多贴3枚邮票可以组合出这么多的资费。这些资费能满足100g以内信函的所有需要吗？

生：表格中的4元、4.8元、6元不能满足。

2.设计邮票，解决问题

师：对于4元、4.8元、6元的资费，只用这两种面值的邮票显然不能满足要求。该怎么办呢？

生11：可以增加1枚更大面值的邮票。

师：你的想法真好，那我们再设计一枚面值为多少的邮票就能同时满足这三种资费的需要呢？接下来我们来一次设计大比拼，开始行动吧！（学生动手设计）

师：哪个小组愿意分享你们的思考过程？

生12：我们设计的邮票面值是2元。因为最高资费是6元，平均分成3份，得出2元；对于资费4元和4.8元，4元可以由2枚2元邮票组合，4.8元可以由2枚2元和1枚80分邮票组合。

生13：我们设计的邮票面值是4元。因为4元、4.8元、6元中最小的是4元，对于资费4.8元和6元，4.8元可以由1枚4元和1枚80分邮票组合，6元可以由1枚4元、1枚1.2元和1枚80分邮票组合。

生14：我们设计的邮票面值是2.4元。我们用平均分的方法，4.8元平均分成2份，每份是2.4元，再用2.4元去试4元和6元的资费，发现都能满足。

师：同学们的回答太精彩了，先确定邮票面值的范围是2元～4元，并会用平均分的方法找到2.4元，再把猜想的数代入另外2个资费里进行验证，经过猜想、验证得出正确结论，真了不起！掌握了这个方法后，400g的信函请同学们课后继续研究。

教学思考：

让学生经历过程相对完整的学习活动，是综合与实践教学的核心。为此，在组织教学时，我给学生留下足够的空间，鼓励学生相互启发，彼此思维发生碰撞。学生在碰撞交流的过程中，学会数学地思考和数学地表达。尤其是在建立“100g内的部分”和“超过100g的部分”分段思考、分段计算的数学模型时，学生全程参与问题的解决过程，积累数学活动经验，提高实践能力，培养数学素养。

当学生对信函分段计费方式有了充分感知，我设计了环环相扣的探究活动。在此探索过程中，学生悟到了解决问题的思路和方法：邮票面值不够用，设计新面值的邮票时，首先确定信函处于不同质量范围内应付的邮资，再根据这些邮资寻找满足条件的邮票面值组合。学生在“做”和“思”的过程中不断磨砺，积累数学活动经验。

（作者单位：慈利县金慈实验小学）