关于“数学思考”的思考

钟德胜

人教版数学教材六年级下册整理复习中有一个内容被称为“数学思考”，是关于“几个点可以连成多少条线段”的问题（具体如图所示）。针对这一内容，笔者有如下思考。

一、“数学思考”的目标是什么

教材在这一内容的开篇部分即指出：“数学思想和方法可以帮助我们有条理地思考，简捷地解决问题。”由此我们可以看出，本内容的基本目标指向数学思想和方法，尤其指向“化繁为简”的方法。这一方法要求我们将复杂的问题简单化，从简单的情形开始研究，通过观察、归纳、概括等活动发现规律，进而解决问题。从这个角度思考，我们不难发现，本节课的教学目标不是要教会学生得出如下问题的答案———平面上有n个点，任意三点都不在同一直线上，将这些点用线连起来，一共可以连多少条线段？

这一问题本身是个简单的组合问题———从n个对象中取2个的组合数。如果学生学习的是排列与组合，将这个问题作为排列与组合的练习题，我们的教学目标就是让学生理解这个问题为什么是“n选2”的组合问题，并直接运用组合公式得到答案。但在这里，我们的教学目标是让学生进一步理解、体会解决这类问题常用的方法，并能熟练使用这样的方法。也就是说，我们的教学目标是指向解决问题的方法，而不是这一具体问题的结果。这个问题只是承载这一方法的素材，我们完全可以换成别的素材———只要素材能承载这一方法。

二、为什么可以“化繁为简”

解决问题时，如果能将问题化繁为简固然很好。把复杂问题简单化，还有什么比这更高明的呢？可我们需要思考，一个复杂问题为什么可以化为简单问题。复杂是复杂问题的特征，简单是简单问题的特征。如何将问题的“复杂”这一特征去掉，进而形成“简单”这一特征呢？

具体到“数学思考”中提出的问题：6个点可以连多少条线段？8个点呢？这是我们所说的复杂问题。其复杂性在于：这里说的6个点、8个点，点数比较多，点数越多越复杂。要化繁为简，就是要把6个点、8个点的问题转化为2个点、3个点的问题。可是，6个点、8个点的问题为什么可以转化为2个点、3个点的问题呢？或者换一个问法：解决一个像2个点、3个点这样的简单问题对解决6个点、8个点这样的复杂问题有什么帮助呢？

事实上，我们所谓的复杂问题，通常是指一个一般问题的特殊情况。比如6个点可以连多少条线段的问题，就是“n个点可以连多少条线段”这个一般问题的特殊情况。我们之所以可以把复杂问题简单化，其实是想通过对简单问题的研究来发现某种一般规律，从而解决一般问题。一旦一般问题得到解决，作为一般问题的特殊情况即复杂问题也就得到解决。

三、如何组织“化繁为简”的教学

一般而言，我们先要对复杂问题做一般化处理。而6个点可以连多少条线段的问题，就是“n个点可以连多少条线段”这个一般问题的特殊情况。接下来，就是从简单开始研究这个一般问题。按华罗庚先生的说法，就是退，足够的退。我们从2个点、3个点开始研究。在此，要特别注意的是，教师应该和学生一起研究，而不是作为一个已知结论的过来人，把获得结论的过程教给学生。具体到这个问题，教师不能过早地把教材中的表格（如下）呈现出来。

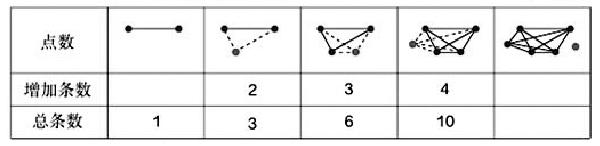
这个表格是发现了规律并已解释为什么有这个规律后的产物，而不是研究问题的产物。

研究问题时，我们分别找出2个点、3个点、4个点能连的线段的总数：1、3、6。按照这一方法做下去，一直到发现某种规律。比如，我们从1、3、6这三个数中发现3=1+2，6=1+2+3时，就可以猜想，接下来可能是1+2+3+4。于是再画5个点的连线图，发现果然是这样。这时回过头来思考，并对这一发现作出解释：为什么是这样？上面的表格就是对这一问题的解释，是发现规律后的事，而不是利用这个表格来发现规律。

规律得到确认，一般问题得到解决，复杂问题也就随之得到解决。接下來要做的事，就是进一步练习使用这个研究方法：再提出一个可以用这个方法研究解决的问题。应当注意的是，巩固练习中的题，不应是与这个问题在内容上类似的问题，比如100个点可以连多少条线段之类，这样的问题对于达成我们的练习目标没有多大价值。

（作者单位：长沙县丁家小学）