估算要讲道理

刘娟 周超民

人教版小学数学教材三年级上册万以内的加法和减法（一）内容中有这样一道题（如图1所示）。

教材上提供了如图2所示的分析与解答。

老师们基本上是按照教材提供的思路进行教学的，但是对其中的理论依据没有作探讨，只停留在表面模仿上。

先看男孩的回答（如图3）。221>200，239>200，两不等式相加，得221+239>200+ 200=400。大于400就一定大于441吗？显然不一定，所以不能确定能不能坐得下。

将上面的过程用不等式表示为：若a>b，c>d，则a+c>b+d。也就是说，同向不等式可以相加。

若m跃b+d，一定有a+c跃m吗？不一定，很容易举出例子来。例如，只要将上面的441改为461=m，461>400=b+d，但a+c=221+239<461，并不是a+c跃m。

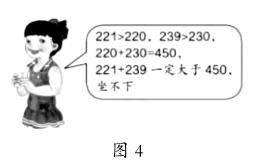
再看女孩的回答（如图4）。221>220，239>230，两不等式相加，得221+239>220+ 230，即221+239>450。而450>441，所以坐不下。

將上面的过程用不等式表示为：若a>b，c>d，则a+c>b+d。如果b+d跃m，则a+c跃m。

教学中，还有老师是这样教的：将221估成220，239估成240，220+240>441，所以坐不下。

结论看起来是对的，其实解法是错误的。错在哪？

将上面的过程用不等式表示为：a>b，cb+d。就错在两不等式相加！a>b，c

从这里可以看出，估算不是拼凑。有的老师由于不了解估算的道理，只要一看到能够凑成整十、整百、整千的数，又能凑出结论，就不管有没有道理了。

综合上面的三种估算方式我们不难发现，估算这样的问题实质就是不等式的简单性质的运用。如，

传递性：若a>b，b>c，则a>c。

同向不等式可以相加：若a>b，c>d，则a+ c>b+d。

异向不等式可以相减：若a>b，cb-d，c-a约d-b。

（作者单位：双峰县永丰镇城南学校）