模糊网络中基于指数的评估函数研究

郑爱媛

（福建商学院信息工程系，福建 福州 350012）

1 引言

传感网络作为一种融合计算机分布式处理技术、物联网[1]通信技术和嵌入式[2]技术于一体的网络体系架构备受欢迎。然而该网络在现实环境中部署时不可避免地受限于周边环境和成本等因素而无法开展，比如，充满压强和声波干扰[3]的深海中，对于一般的GPS装置节点而言显然无法投放。诸如此类的局限势必导致全局参数较为变幻莫测。因此，在这类模糊网络环境中探索QoS异常的目标节点相关评估技术，也就成了研究的方向。比如，通过一定的计算机制对传感网络中QoS较弱的目标进行评估。实施该计算机制可通过其附近节点广播的精确位置和跳数等信息域来辅助实现。可见，信标节点在全局网络中广播的信息域决定了QoS异常的待测目标是否被精确评估。

目前对于上述这类基于坐标和跳数作为参考依据开展分布式[4]计算的机制较为流行，常见的研究方法有：（1）通过一定的算法对模糊网络提供的模糊信息域进行追溯计算，还原出精确的信息域，进而精确地推算出目标坐标；（2）引入纠错机制，对全网所有节点的模糊跳距进行平均化以达到差错控制目的。然而，上述主流研究方法的研究对象特征要么为节点密度分布较为均衡的情形，抑或是通信半径范围内的单跳情形。无论何种情形，此类研究方法终究因研究对象特征的偶然性而无法推广。尤其当模糊网络中节点规模较大且分布无规律可言时，所评估的节点间距将出现严重的误差偏向。鉴于此类主流算法的局限性[5]，本文提出一种在模糊网络环境中引入指数的评估函数，用于评估在随机密度的模糊环境中多跳情形下的信息域。

2 指数级评估函数

援引传统的DV-Hop计算机制，其计算准则为所有跳距的加权值和跳数的乘积作为信息域中间距的评估值。实现过程分以下三个步骤开展分布式计算：

步骤一：初始化跳数计数器。

步骤二：全局模糊网络中载有GPS装置的信标i，广播本地坐标和跳数信息域(Xi，Yi，Hi)[6]。位于该信标源点通信半径范围内的信宿节点保存该信息域并将计数器赋值1，同时广播信息至周围邻居节点。当信宿节点曾经保存过同样信标源点广播的信息域且跳数超过本地内存中的跳值时，则不再接收新的信息域。依此循环直至遍历到全局节点均获取到包含最小跳数(Xi,Yi,Himin)的信息域。

于是，可求得信标i的每个跳距加权值：

步骤四：信标广播本地跳距加权值至全局。对于待测目标节点而言，仅保存最近的一个邻居信标向其广播的跳距加权[7]值于本地内存中，并将此跳距加权值转发至下一个节点。

步骤五：评估出未知节点u与信标i间的间距：

步骤六：根据式3求得未知节点与三个以上信标之间的间距估值，再通过极大似然[8]法评估出未知节点u的坐标。

由于在模糊网络中，网络结构及其节点密度均为不可预测。这样的应用环境中，通过第五个步骤的计算方式求取的间距评估值与间距实际值存在一定的误差偏向[9]。尤其在跳数较多的情形下，间距评估值将随着误差累积性作用而加剧估值的误差偏向。针对这样的状况，现有的研究方法主要是将节点的通信半径视为一跳的跳距，即理想一跳的跳距。在此基础上定义实际跳距相对于理想一跳跳距的误差偏向：(RLu)/R，并由此展开了对未知节点u坐标的差错控制[10]评估：

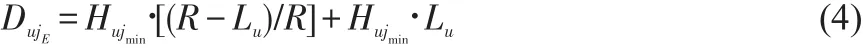
再通过极大似然法评估出经差错控制后的未知节点u的坐标。

然而一跳情形下的研究方法并不总是适用于模糊网络，因此本次研究了多跳情形下为提高待测目标估值精确度，引入指数λ的评估函数来校正信标j和未知节点u之间最小多跳HSuimin情形下的误差偏向：

3 指数的研究

指数λ的取值因环境而有所不同。为了定义合适的指数赋值用于评估未知节点的坐标，本次在长宽均为100M的模糊网络中随机投放200个节点，其通信范围R统一定义为20M。通过为指数赋不同数值再经由Matlab测试[11]后选择最优值。测试结果如图1所示。

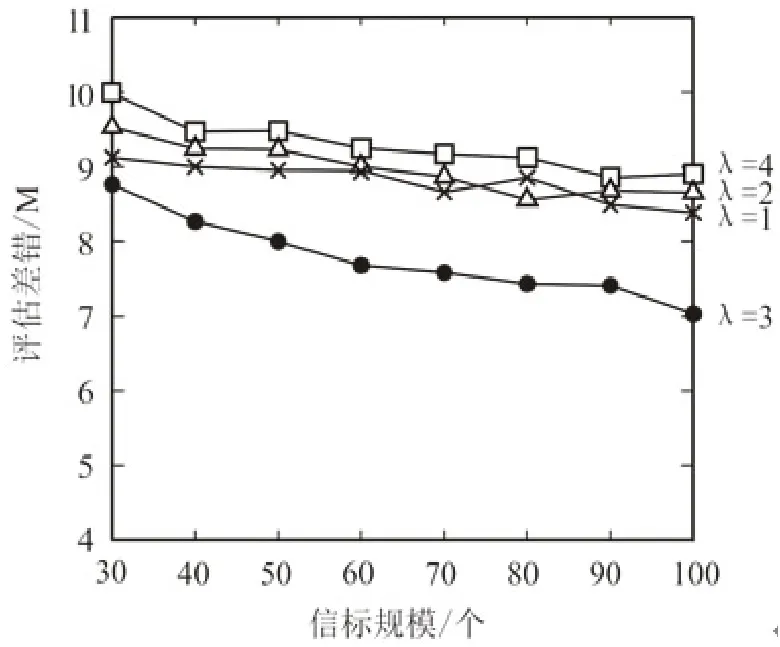
图1 指数与评估误差的关系

由图1曲线走势可见，当为指数赋3值时，评估误差最低。为进一步精确指数赋值，开展了如图2的测试。

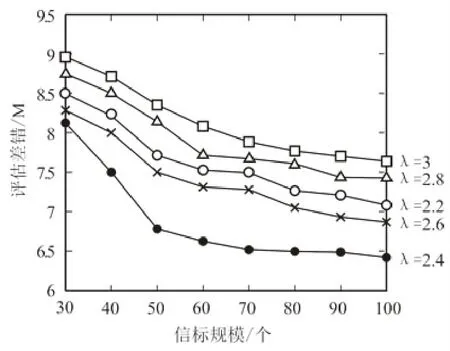
图2 不同赋值与评估误差的关系

由图2不难看出，当为指数赋2.4值时，评估性能最优。同时由误差偏向的表达式[12]可见，多跳情形下的评估差错程度与通信范围R也呈现函数关系。经过多组测试数据表明，指数赋值也随着R的扩大而线性递减。由此可评估出信标j和未知节点u的在多跳情形下的间距为：

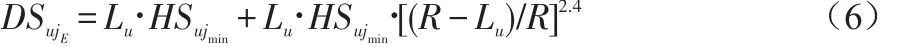
可得，信标j和未知节点u符合关系式：

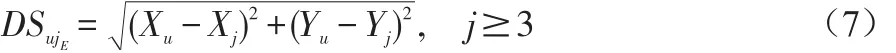
再利用最小二乘法[13]计算出u(Xu，Yu)。

4 评估函数的实施

在模糊网络环境中，多跳情形下实施嵌入指数的评估函数旨在进一步降低信标和未知目标之间的评估距离。该函数在实施前由信标向全局广播信息域。信宿节点保存该信标的信息域后对信标后续广播的数据进行比较取舍，确保获取最小跳数。其次，未知目标读取最近信标发送的每个跳距加权值和多跳情形下的评估间距。最后完成评估u(Xu，Yu)的实施[14]。整个评估函数的实施流程如图3所示。

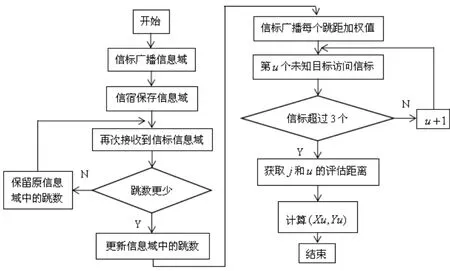
图3 评估函数实施流程

5 评估函数的测试

5.1 测试模型

为确保评估函数的顺利实施，首先需要搭建测试模型[15]对评估函数展开相关测试，测试开始前先对仿真模型和相关指标[16]做如下设置：（1）构建100M×100M的待测模糊传感网络，并在全网范围内按照20:200的比例随机撒布信标/总节点；（2）设定通信半径变化区间分别为[20M,45M]；（3）假设全局网络存在Nu个未知目标，且未知目标的估值坐标和实际坐标为 uE(XuE,YuE)、u(Xu，Yu)，则归一化差错幅度表示为

制定的测试方案主要通过变换节点规模、通信范围考察评估函数的评估差错程度。为凸显本文研究方案的优势，测试过程将评估函数与传统计算机制、现有的单跳研究方法展开对比分析[17]。

5.2 测试分析

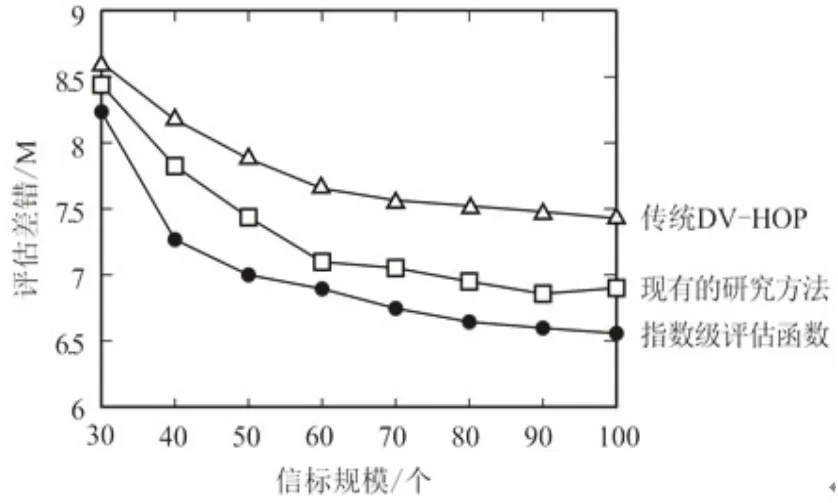
图4 信标规模与评估差错关系

图4所示为信标从20个的规模逐渐增至100个规模过程中，三种评估机制下未知目标评估的差错幅度曲线走势[18]。图中可见，当信标规模较小时，三种机制下的差错幅度总体较大，且彼此间的层次较为接近。随着信标规模增加，未知目标节点获取到了更多更精确的信息域，于是伴随着三种机制评估差错的收敛。虽然现有的研究方法也能对待测目标和信标之间的跳数与跳距进行评估，但是由于这样的研究方法主要适用于单跳情形。而本文提出的评估函数优势在于引入的指数参数可在不同信标规模的环境中良好地实施跳距评估。因此，在评估差错指标中表现最佳。

图5所示为在相同的通信范围和信标比例[19]下，当总节点从200个规模递增至300个规模时，三种评估机制下的归一化幅度。不难看出，三种机制下的归一化幅度均与总结点规模呈现反比关系。出现这样走势主要因为在模糊网络面积恒定的前提下，撒布的节点总数量越多，则单位面积内的密度显著增大，伴随着广播的信息域精度越高，归一化误差也就越小。在良好的信息域环境中，指数的引入则进一步对测距数据做了改善。因此相对其他两种机制而言，评估函数占据优势。

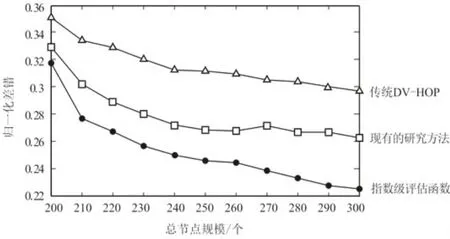
图5 总节点规模与归一化差错关系

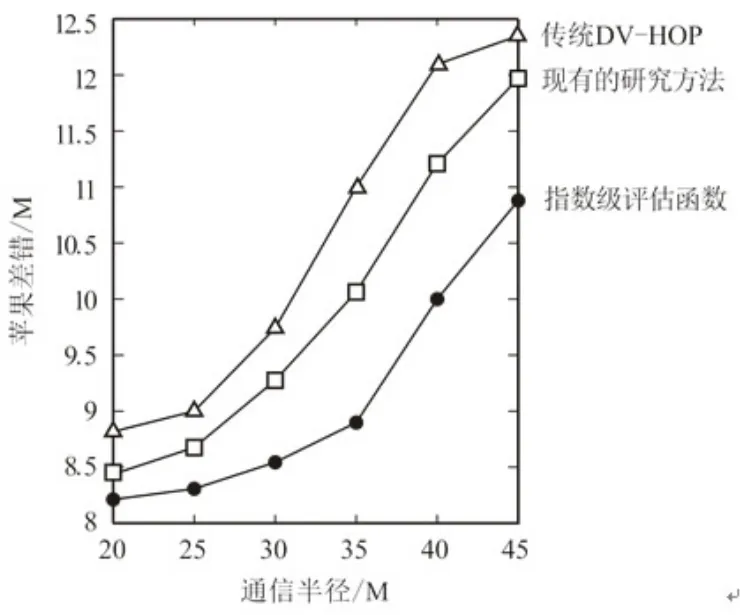
图6 通信半径与评估差错关系

图6所示的曲线走势是在保持各类型节点规模不变的前提下，通信半径遵循区间[20M,45M]变化时，三种机制的评估差错程度。随着节点通信半径增加，待测目标接收到的信息域中的跳数以及跳距等参数存在错误的概率也是线性递增。伴随通信半径的进一步增加，跳数和跳距的参数误差将被进一步累积[20]。当信宿节点将累积性误差的信息域传达至周边节点时，必然引起全网定位失效。因此随着通信半径的增加，评估差错程度势必陡增。这样的特征在图示中的走势均得以体现。但是由于本文提出的评估函数引入了参数，适用于多跳情形下的跳数、跳距评估，因此当通信范围越大，越有利于评估函数优势的发挥。

6 总结

本文通过对传统计算机制和主流研究方法运用在模糊网络环境中，开展目标评估可行性较低的情形，提出了一种适用于多跳情形下的评估函数。该函数通过一定的机制赋值函数中的参数实施跳数和跳距的评估，进而实施待测目标的精准计算。最后，经过仿真平台测试证明本文研究的评估函数具有良好的优势。