基于响应面法的机床床身动力学模型修正*

邵莹河，洪荣晶，于春建

(南京工业大学 机械与动力工程学院，南京 211800)

0 引言

有限元分析技术已成为工程结构分析的重要手段，基于有限法的结构分析软件的出现，使运用有限元法来获取结构的动静态特性变得更加便捷。在建立有限元模型时，因对结构的简化和边界条件的假设等，造成动力学模型与实际对象有一定的误差产生，其误差可以分为三类：模型结构误差，模型参数误差和模型阶次误差[1]。当模型结构或者边界条件复杂时，分析结果与实际结果有较大的出入。建立准确的动力学模型是利用有限元法进行结构分析和性能评价的前提，特别对于动态特性要求较高的结构而言更加重要，如机床、航天器等。对于结构动力学模型的修正已成为结构动力学研究的重点。

响应面法具有便捷、可操作性高、适应性强等特点，现已广泛应用于解决设计变量和优化目标之间函数关系不明确时的优化问题。如张疆平等[2]采用自适应响应面法对肋板厚度和壁厚尺寸进行优化，提高了机床前两阶固有频率，表明该方法可实现机床快速优化设计。王万金等[3]将网格变形技术与响应面法相结合的方式，实现了机床床身的轻量化优化设计，体现了该方法具有较高的操作性。M R Stalin John等[4]采用响应面法对加工中心磨削参数进行了优化，获得了最佳加工参数。

近年来，已有学者对机床的动力学模型修正作出了相应的研究，如巫修海[5]建立了加工中心整机的动力学模型，并对修正参数进行了灵敏度分析，确定了零件间的连接特性灵敏度较高，并对此进行了调整，使整机有限元模型求解与实际动力学特性相符。然而其对修正参数的调整并未应用优化方法，所取参数值并非最优值，有一定的优化空间。葛泽稷等[6]以弹簧单元模拟床身与地基之间的边界条件，并以弹簧刚度值为修正参数，以固有频率的最小二乘法为目标函数建立了优化模型，实现了床身动力学模型修正，但是他们只对床身垂直连接刚度进行了修正，并未考虑水平方向的刚度，且优化迭代时需要求解有限元模型，增加了计算量。

针对以上问题，本文提出了一种基于响应面法对床身动力学模型进行修正的方法。以CLFH-200齿轮复合机床床身为研究对象，以ANSYS Workbench中地基刚度模拟床身与垫铁地基系统的三方向连接刚度，对床身垂直及水平方向的连接刚度进行修正。并建立三方向刚度与固有频率之间的响应面模型，避免每次迭代对有限元模型进行求解，减少了计算量。采用二次规划法对响应面模型进行优化，获得三方向的最佳刚度值，从而达到对床身动力学模型修正的目的。

1 机床床身初始模型建立

动力学模型修正的目的是缩减有限元分析结果与实际响应的误差，本质上属于结构优化范畴，设计变量即要修正的参数，优化目标即修正评价标准，再通过优化算法达到模型修正的目的。对动力学模型的修正主要集中在消除模型的参数误差[7]，如模型的物理参数(弹性模量，密度等)和边界条件等。对于动力学模型修正的优化目标选择主要集中在三方面：①模态参数；②频响函数；③动力学响应。其中固有频率测量最为容易且精度较高。以固有频率为修正目标能较为快捷的得到准确度较高的动力学模型。

建立床身初始动力学模型，该床身为箱型结构，总长1970mm，宽1300mm，高585mm。内部分布有十字肋板，四周分布有方形及圆形减重孔，为便于切削液及切屑的流出，上部床板进行倾斜设计。根据圣维南定理，对机床床身的细小工艺特征进行简化，简化后的机床床身如图1所示。

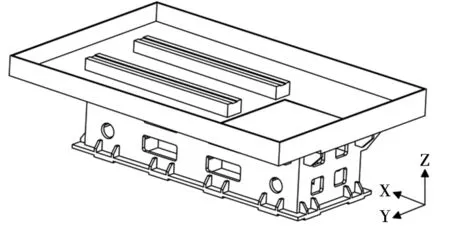
图1 床身简化模型

床身材料为Q235A，弹性模量为E=2.12×1011Pa，泊松比为0.288，密度为7860kg/m3。由于床身的结构复杂，采用自动网格划分方法，网格相关度relevance为100，相关度中心设置为fine，经过调试，最终得到的有限元模型如图2所示，其中单元类型为solid187，单元数为50128，节点数为95809。在不确定连接刚度的情况下，可设置床身与垫铁接触 面为全固定约束。

图2 床身有限元模型

2 模态试验

模态锤击试验，采用LMS Test.Lab 振动测试系统，其锤击系统组成原理如图3所示，其中数据采集选用LMS SCADAS Mobile Front-End (8通道输入数采前端+2通道源输出+2通道转速输入)，加速度选用传感器美国PCB公司的ICP三向加速度传感器，其灵敏度100mV/g, 量程50g, 频率范围 0.5～3000Hz，力锤选用美国PCB公司的模态ICP5000lbf力锤，其锤头1.1kg重，含ICP型力传感器一只，灵敏度为1mV/lbf (0.23mv/N)，响应范围 0～5kHz，BNC接头。

图3 锤击模态试验原理图

采用原装支撑方式，根据床身的刚度分布情况，合理分布测点，将床身分为28个测点，为便于测试选择移动传感器的方式进行测量，锤击点选择方便锤击且刚度相对较大的位置[8]。现场布置如图4所示。

图4 试验现场布置图

根据初始模型分析结果，选择所关心的前6阶固有频率范围，经过多次测量，采集数据后传到PC机分析可得前6阶固有频率，结果如表1所示。

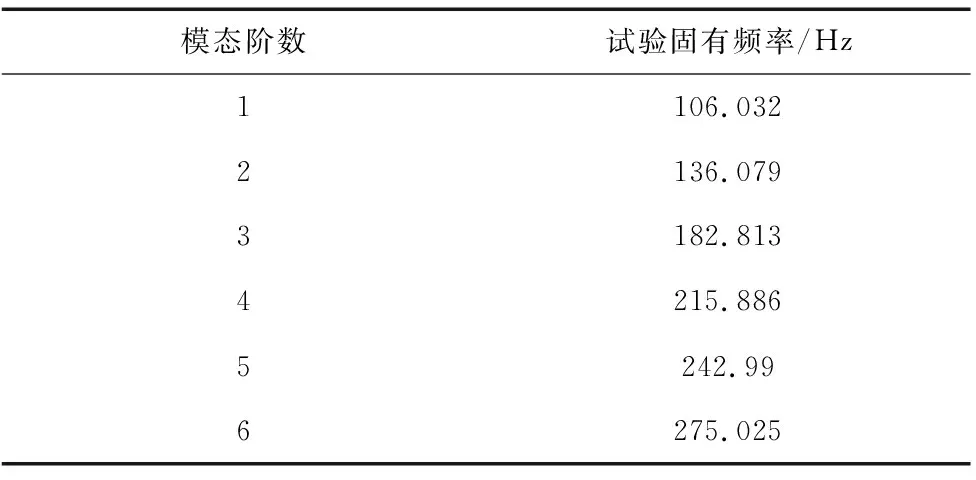
表1 试验固有频率

3 模型修正

在床身结构和材料确定的条件下，其边界条件对有限元模态分析影响较大，由于床身是经过垫铁与地基相连，其接触面的刚度难以确定，为了简化处理过程一般采用全固定约束，与实际情况有一定误差，造成了有限元模态分析结果与实际试验结果的偏差。本文用ANSYS Workbench中的地基刚度选项，模拟床身与垫铁地基系统的接触刚度。由于床身固定处x、y方向约束情况相似，对其刚度值做等值处理，故刚度可简化为z方向刚度和x、y方向刚度，经过分析初步确定3方向的变动范围如表2所示。

表2 刚度的取值范围

为使固有频率误差最小，以刚度值为设计变量，固有频率最小二乘法为目标函数建立响应面模型[9]，构建地基刚度与固有频率误差的相互关系。其修正流程如图5所示。

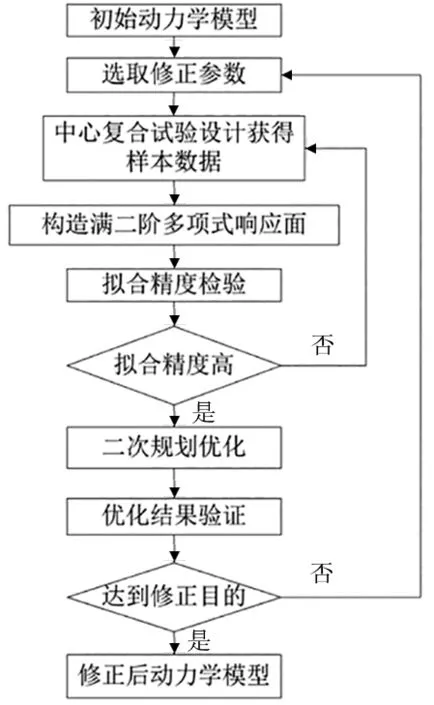
图5 模型修正流程图

3.1 试验设计

中心复合试验设计(CCD)[10-11]是拟合响应面的最常用的方法，可有效的评估因素的非线性影响及因素间的交互作用，采用中心复合表面设计(CCF)获得数据点，其轴心点取1，将每个因素分为3个水平，可有效的得到试验点分布，试验点分布情况如图6所示。

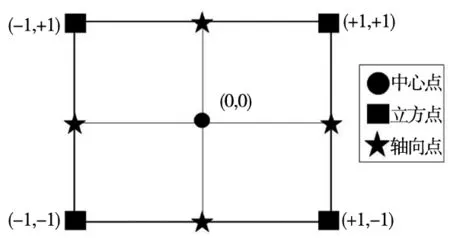
图6 试验点分布

图6中+1、-1分别对应试验点的上下限，按试验点取值范围和分布情况进行9次有限元分析，试验结果p是由固有频率最小二乘法得到，如式(1)所示：

(1)

式中，fi为有限元分析中的第i阶固有频率，Fi为试验模态中第i阶固有频率。

最终得到试验结果如表3所示。

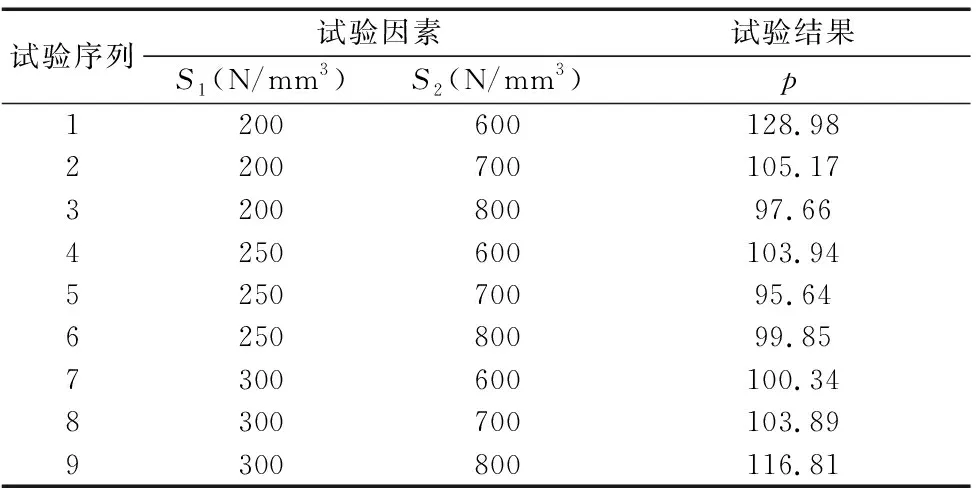
表3 床身中心复合表面实验设计结果

3.2 建立响应面模型

采用满二阶多项式法建立响应面模型，其数学表达式如式(2)所示：

(2)

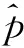
由最小二乘法确定回归系数，最终拟合得到响应面公式如式(3)所示，该响应面模型如图7所示，

p(s) = 1082 - 3.508s1- 1.52s2+ 0.002389s1s2+

(3)

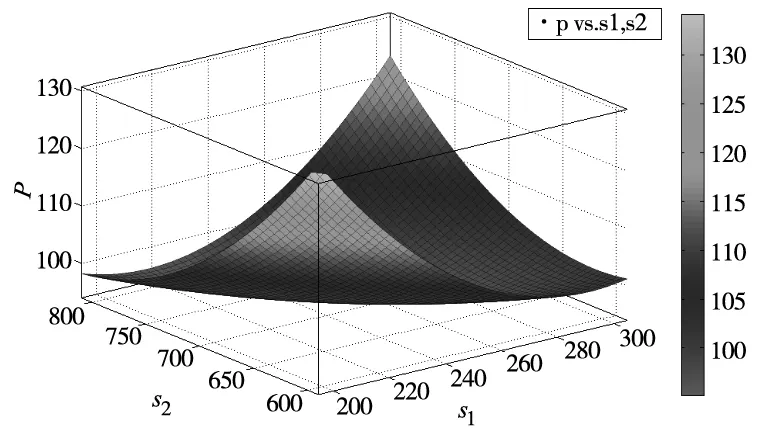
图7 响应面模型

对回归模型进行F检验和确定系数检验[12]，结果如表4所示，确定系数接近于1，表明该模型拟合程度较好，可进行下一步优化。

表4 误差检验

3.3 响应面模型优化

以响应面模型为优化目标函数，刚度为设计变量，得到其修正数学模型如式(4)所示：

minp(s)=p(s1,s2)
s.t. 200≤s1≤300
600≤s2≤800

(4)

二次规划法是目前最先进的非线性规划计算方法之一[13]。经计算最终得到最佳刚度值s1为241.25N/mm3，s2为741.52 N/mm3，并带入有限元分析模型。修正后的动力学模型固有频率和误差如表5所示。

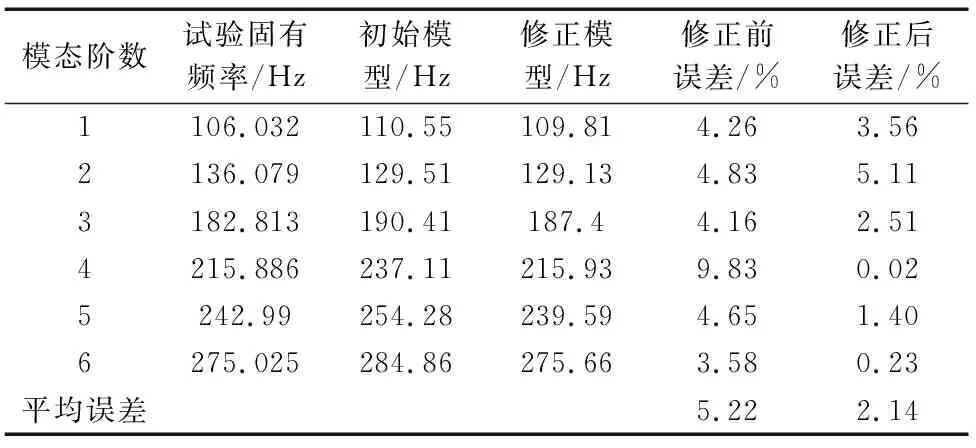
表5 修正后固有频率对比

修正后动力学模型的固有频率与试验频率之间的总误差明显减小，与初始模型固有频率误差相比，第1阶误差降低了0.70%；第2阶误差增加了0.28%，虽然有所提升，但对于整体来说并不显著，可能由于实际床身局部焊接焊缝所造成的影响；第3阶误差降低了1.65%；第4阶降低了9.81%；第5阶误差降低了3.25%；第6阶降低了3.35%。优化后最大误差为5.11%，最小误差仅为0.02%。整体来看，平均误差由5.22%降到了2.14%，降低了3.08%。结果表明修正后各阶频率误差相对较小且都在合理范围内，修正后的动力学模型可靠性得到了提高。

4 结论

本文提出的基于响应面法对床身动力学模型进行修正的方法， 以ANSYS Workbench中地基刚度模拟床身连接刚度，简化了对与边界条件的处理过程，并以此为设计因素，通过中心复合试验设计拟合得到满二阶多项式响应面模型，并对其拟合精度进行了检验，避免了每次迭代对有限元模型进行求解，提高了优化效率。采用二次规划法对响应面模型进行优化，可以有效的得到最佳刚度数值，修正后床身动力学模型的前6阶固有频率平均误差由5.22%降到了2.14%。实现了动力学模型修正，为床身动力学模型修正提供了一种便捷有效的方法。