虚拟惯性时间常数对互联电网小干扰稳定影响研究*

陈中，殷大朋，朱英凯，周涛，施志强

(1.东南大学 电气工程学院，南京 210096；2.江苏省智能电网技术与装备重点实验室，南京 210096； 3.南京供电公司，南京 210000)

0 引 言

区域电网互联成为当前电力系统发展趋势[1-2]，低频振荡问题成为影响系统运行安全的重要因素[3-5]。目前低频振荡工作主要集中于控制器设计、在线控制[6-10]，但对于惯性时间常数影响研究较少，其原因在于传统电力系统中同步发电机的惯性常数是不变的物理参数。文献[11]利用Eurostag软件进行时域仿真，研究了转动惯量对互联电网暂态稳定性的影响；文献[12]研究了两端电网惯量变化对系统暂态稳定水平的影响与运行方式的关系，但都没有涉及小干扰稳定。

随着柔性直流输电(VSC-HVDC)、可再生能源的发展，以及电力电子技术的广泛应用，虚拟同步发电机技术(Virtual Synchronous Generator, VSG)的示范推广使得转动惯量成为灵活可调的参数[13-17]。在电力系统中应用虚拟同步发电机技术是为了提高通过电力电子并网设备的调频调压特性，目前对于惯性时间常数和阻尼系数的研究主要从电力电子本体的动态响应性能出发，而没有考虑对电力系统稳定性的影响。文献[15]研究了微网逆变器的虚拟同步发电机模型，使得逆变器在并网时具有功率控制功能，离网时具有电压频率控制特性；文献[16]基于VSC-HVDC换流站建立虚拟同步电机模型，在虚拟调速器中加入了频率偏差积分环节，实现了换流站的二次调频功能；文献[17]提出了变速风电机组的虚拟惯性控制策略，并分析了该惯性对风机本体功率振荡的抑制能力。虚拟同步发电机技术的应用使得惯性时间常数成为电网可控参数，以致利用这一参数的调节能力提高小干扰稳定性成为可能，为此，有必要研究惯性时间常数对系统低频振荡的影响及其控制方案。

首先对VSC-HVDC逆变侧换流站进行虚拟同步发电机建模；其次对联网等值系统线性化处理，求出低频振荡衰减因子的解析表达式；然后分析了不同场景下惯性时间常数对小干扰稳定水平的影响程度，最后在两区四机经典模型中进行算例仿真验证结论，对于研究虚拟同步发电机参数整定和互联系统的区域振荡稳定性分析及控制具有一定的参考价值。

1 VSC-HVDC逆变站虚拟同步发电机控制

将VSC-HVDC逆变站模拟为同步发电机，可以增加转动惯量，为电网提供动态频率支持，换流站控制结构图如图1所示，其中VSG算法模块正是其控制核心。

借鉴同步发电机二阶模型，并取发电机极对数为1，则电气角速度与机械角速度相等，记电气角速度为ω，虚拟同步电机的转子运动方程为：

(1)

式中δ是同步发电机的功角；Pm和Pe分别是发电机的机械功率和电磁功率；Tj为惯性时间常数；D为阻尼系数；ω0为电网同步角速度，其标幺值为1。

图1 虚拟同步发电机结构图

传统发电机的调速器通过响应频率偏差，调节汽轮机汽门或水轮机导水叶开度，改变了机械功率，基于该原理，虚拟同步发电机的虚拟调速器方程为：

Pm=Pref+kω(ω0-ω)

(2)

式中Pref为换流站的有功功率输入值;kω为调频系数。由转子运动方程式(1)和虚拟调速器方程(2)可得：

(3)

由式(3)可知，在虚拟同步发电机的模型参数中，调频系数与阻尼系数起共同的阻尼作用，和常规发电机组的自身阻尼类似，值越大，低频振荡的阻尼系数越大，越有利于低频振荡的衰减。

2 惯性常数对低频振荡影响机理

分析VSC-HVDC并网互联系统稳定性问题时，可将各区域电网内的常规发电机组等值为一台同步发电机组，在含有虚拟同步发电机的区域内，该区域惯性时间常数可调，整个系统可视为两台虚拟同步发电机连接的等值两机系统，两机系统等值电路如图2所示。

图2 两机系统等值电路

虚拟同步机采用经典二阶模型，并考虑阻尼，每台发电机的转子运动方程为：

(4)

式中δi和ωi分别为第i台发电机的功角和角速度；TJi为惯性时间常数；Di为阻尼系数；Pmi为机械功率；Pei为电磁功率。

对两机系统线性化，得到其状态方程：

(5)

式中 Δδi和Δωi分别为第i台发电机的角位移增量和角速度增量；Kij=∂Pi/∂δj。

式(5)的特征方程可表示为：

λ(λ3+kλ2+mλ+n)=0

(6)

特征方程有一个零根，一个实根，一对共轭复根，记共轭复根为：

λ1,2=σ±jω

(7)

式中σ为振荡模态的衰减因子，反映了振荡的衰减程度，其值为：

(8)

式(8)中各个参数表达式如下：

(9)

(10)

(11)

(12)

(13)

将衰减因子σ分解为σ1、σ2之和，σ1和σ2的表达式分别为式(14)和式(15)：

f1(Tj1,Tj2,D1,D2,K11K12)

(14)

(15)

由式(15)可以发现：

(1)σ2为Tj1、Tj2、D1和D2的函数，其值仅与虚拟发电机本体参数有关；

(2)σ1为Tj1、Tj2、D1、D2、K11和K12的函数，其值与发电机参数和系统运行方式相关；

(4)当惯性时间常数与阻尼系数在同一个数量级时，此时σ1的值不能忽略，σ1与σ2共同决定了σ，惯性时间常数变化对低频振荡的衰减因子影响较大，由于σ1的存在，σ呈现非线性，惯性时间常数的影响应根据实际电网进行具体分析。

3 衰减因子随惯性时间常数的变化规律

为分析惯性时间常数对低频振荡衰减因子的影响，在Matlab软件中搭建了图2所示的两机系统，进行了3种场景下的衰减因子随惯性时间常数的变化的仿真：场景(1)两台发电机参数相同，潮流对称；场景(2)两台发电机参数相同，潮流不对称；场景(3)两台发电机参数不同，潮流不对称。衰减因子随惯性时间常数的变化如图3所示。

图3 σ随惯性时间常数的变化规律

通过图3，将场景(1)～场景(3)对比发现：

(1)当惯性时间常数比阻尼系数大一个数量级时，惯性时间常数的变化对衰减因子σ影响较小，总体呈现阻尼随惯性常数增大而微弱减小的趋势，因此重点关注阻尼系数的影响；

(2)当惯性时间常数和阻尼系数是同一数量级时，惯性时间常数的变化对衰减因子σ影响较大，尤其是惯性时间常数较小时影响很大，并且具有非线性，因此需要结合具体场景重点关注惯性时间常数和阻尼系数的共同影响。

4 仿真验证

应用Matlab软件在经典的两区四机系统中进行仿真，两区四机系统结构如图4所示。将两区四机系统的G1和G4换为VSC-HVDC的逆变站，其中G1和G4为虚拟同步发电机，即G1、G4的惯性时间常数和阻尼系数可调。

图4 两区四机系统模型

假设联络线节点8处在0.1 s时发生瞬时三相短路故障，故障在0.01 s后切除，设置G1、G4的惯性时间常数较小值为TjL，较大值为TjH，设置G1、G4的阻尼系数较小值为DL，较大值为DH。其中，TjL和DL所在数量级相同，TjH比DL大一个数量级。设置6种参数设置方案下的仿真，具体参数设置方案如表1所示，并观察区域振荡模态特性，仿真的功角差波形如图5所示，模态计算结果如表2所示。

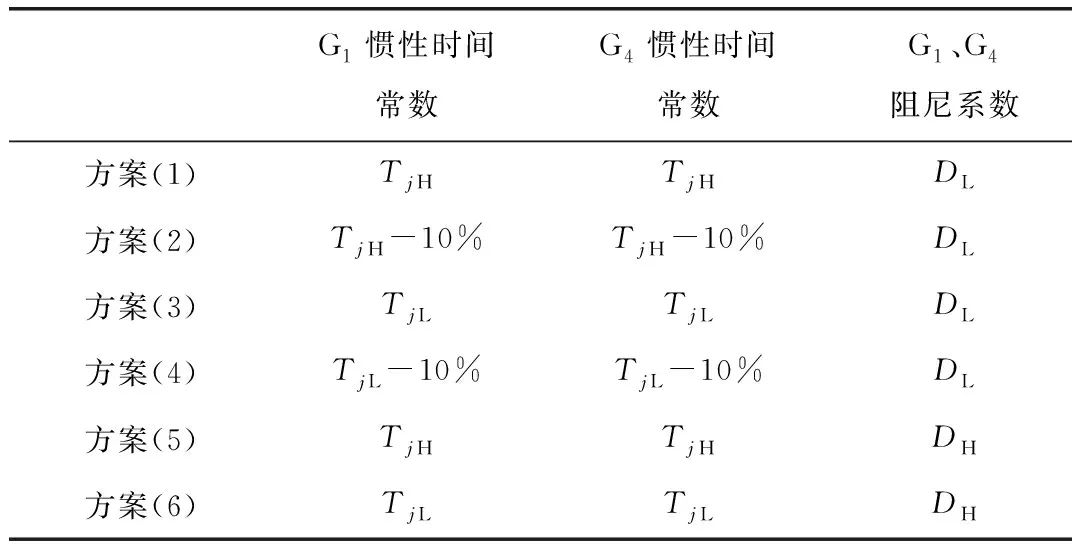
表1 仿真参数

图5 G1～G3功角仿真波形

区域模态衰减因子阻尼比方案(1)-0.054 1+i3.029 4-0.054 10.017 9方案(2)-0.059 9+i2.959 0-0.059 90.020 2方案(3)-0.127 8+i2.955 5-0.127 80.043 2方案(4)-0.148 3+i2.844 5-0.148 30.052 1方案(5)-0.164 9+i2.822 0-0.164 90.058 3方案(6)-0.196 9+i2.777 3-0.196 90.070 7

根据图5(a)中方案(1)和方案(2)和表2中模态计算结果可见，当惯性时间常数比阻尼系数大一个数量级时，当惯性时间常数的变化10%时，衰减因子σ变化仅约0.006，变化较小，因此，惯性时间常数对小干扰稳定性水平影响较小。

根据图5(b)中方案(1)和方案(5)和表2中模态计算结果可见，当惯性时间常数比阻尼系数大一个数量级时，由于惯性时间常数对衰减因子的影响较小，仅阻尼系数对惯性时间常数对衰减因子的影响较大。

根据图5(c)中方案(3)和方案(4)和表2中模态计算结果可见，此时惯性时间常数与阻尼系数在同一个数量级，当惯性时间常数的变化10%时，衰减因子变化近0.02，变化较大，因此，惯性时间常数对小干扰稳定性水平影响较大。

根据图5(d)中方案(3)和方案(6)和表2中模态计算结果可见，此时惯性时间常数与阻尼系数在同一个数量级，阻尼系数对衰减因子影响较大。

5 结束语

对VSC-HVDC换流站进行虚拟同步发电机建模，基于特征根分析法，研究了惯性时间常数对互联电网小干扰稳定性的影响，得出以下结论：

(1)当互联电网的惯性时间常数与阻尼系数数值在同一个数量级时，惯性时间常数对低频振荡的衰减因子影响较大，当惯性时间常数增大到大于阻尼系数数值所在数量级时，惯性时间常数增大对低频振荡衰减因子的影响减弱，衰减因子的幅值增长趋于平缓；

(2)虚拟同步发电机的应用使得系统惯性时间常数和阻尼系数可调，在整定虚拟同步发电机的惯性时间常数时，应考虑到惯性时间常数与阻尼系数数值是否在同一个数量级，当在同一个数量级时，应当同时考虑惯性时间常数对本体小信号稳定性和对系统小干扰稳定性的影响。

文中研究惯性时间常数对电力系统小干扰稳定的影响，今后可进一步结合惯性时间常数对暂态稳定性的影响，实现小干扰稳定性、暂态稳定性的协调和协同控制，以及利用虚拟同步电机技术提高系统暂态、动态、静态稳定性等。