含大规模屋顶光伏电站接入农村配电网多目标优化配置方法*
2018-12-04刘海涛许伦郝思鹏张潮高宇
刘海涛,许伦,郝思鹏,张潮,高宇
(1.南京工程学院,南京 211167; 2.国网江苏省电力有限公司江都区供电分公司,江苏 扬州 225200)
0 引 言
伴着光伏发电技术不断提高、成本持续降低,以及国家一系列促进光伏电站发展政策的出台,加深了全社会对于光伏发电产业的认同感,使得用户加入分布式光伏发电成为可能[1]。农村地区由于大量闲置的面积,建设屋顶光伏电站潜力巨大。考虑到未来的光伏能源的发展,城市地区安装条件的限制,以及农村负荷对于供电质量的要求不断提高等因素,进行农村配电网分布式屋顶光伏电站优化配置具有必要性。
在已有文献中,针对小容量的屋顶光伏电站接入配电网选址定容分析还属于空白,亟待填补。文献[2-3]针对外部因素对屋顶光伏电站发电效率影响进行了分析,文献[4]针对安阳市20 kW工程实际案例,综合考虑光伏安装地区的温度、湿度、光照辐射、安装倾斜角,分别分析了工程经济效益、环境效益、社会效益。文献[5]以小容量光伏电站的收益率、投资回收期、全寿命净收益为指标,建立经济性分析模型,并以用户为中心进行分析验证。文献[6]通过PVsyst软件模拟小容量光伏电站的发电量,结合上海地区实际用电类型、屋顶安装方式以及补贴政策进行经济性分析。
以上文献都是以小容量光伏电站的经济性指标为主结合其他因素进行分析,未考虑到大规模屋顶光伏电站接入配电网后对系统的影响。文献[7]为简化分布式发电选址定容分析模型,一阶段采用经济性指标结合权值系数得到选址结果,二阶段应用粒子群算法以经济成本为目标函数确定配置容量,这种方法虽然简化了选址定容的计算复杂度,但选址和定容过程没有同时进行,容易忽略最优解。文献[8]考虑了分布式电源和负荷的时序特性,结合峰谷电价,以配电网网损费用最小为目标函数进行选址定容分析,这种方法可以精确反映配电网运行特征,使得选址定容结果更为合理,但是本文所研究的屋顶光伏电站单个容量远远低于传统分布式电源容量,其时序性对配电网的影响较小,为简化分析过程可以忽略。
基于以上分析,以IEEE-33节点配电系统为构架,以屋顶光伏电站建设投资成本最小化和系统网络损耗最小化同时进行优化,综合考虑农村地区安装面积限制和配电网运行约束,构建了含大规模屋顶光伏电站接入农村配电网双目标优化配置模型,并且应用针对高维度解改进的NSGA-II算法进行优化,最终通过模糊贴近度筛选出最优方案,并通过算例验证该方案在满足经济性的同时对供电可靠性的影响。
1 屋顶光伏电站优化配置模型
1.1 屋顶光伏电站建设运行总成本
在文献[9]的成本模型基础上,考虑工程的收益周期,引入资金时间价值和设备残值以及维护费用,更加准确地反映屋顶光伏电站建设运行投资的实际情况:
Call=C1+C2+C3
(1)
式中Call为屋顶光伏电站建设运行投资;C1为初始投资成本;C2为运行成本;C3为报废时设备残值。初始投资成本C1主要取决于配件成本和装机容量,即:
C1=Csp·n+Cst+Civ+Cec+Cp
(2)
式中C1为光伏电站初始投资成本;Csp为太阳能电池板单位瓦数价格;n为屋顶光伏电站容量;Cst为支架总成本;Civ为逆变器价格;Cec为输配设施价格;Cp为底座成本。
运行成本C2主要由设备维护成本构成,并且考虑资金时间价值,即:
(3)
Cma=C1K
(4)

报废时设备残值C3主要由初始投资决定,即:
(5)

1.2 系统网络损耗模型
在考虑农村配电网中屋顶光伏电站的接入位置以及容量时,以系统网络损耗为衡量农村配电网电能质量的指标,有:

(6)
式中Ploss为配电系统网络损耗;l为系统支路数;rk为系统k支路电阻;Ik为系统k支路通过的电流。
1.3 屋顶光伏电站布点模型
对于n个节点构成的配电网络,采用0-1整数规划配置模型的位置,用n维向量x=[x1,x2,…,xn]表示屋顶光伏的配置情况[10]。其中:
(7)
1.4 约束条件
(1)功率平衡约束
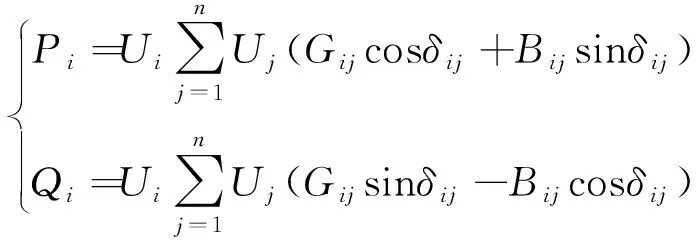
(8)
式中Pi、Qi为节点i向系统注入的有功功率、无功功率;n为系统的节点数;Ui、Uj为节点i、j电压向量的幅值;Gij为节点导纳矩阵元素Yij的实部;Bij为节点导纳矩阵元素Yij的虚部;δij=δi-δj,为i、j两节点电压的相角差。
(2)电压约束
UminUUmax
(9)
式中Umin和Umax为节点电压允许的上下限,一般电压正、负偏差的绝对值之和不超过额定值10%。
(3)屋顶光伏电站容量约束
设定屋顶光伏电站功率在15 kW以下,为了保证供电可靠性,接入节点的屋顶光伏有功功率不能超过节点负荷的30%,总的屋顶光伏有功功率不能超过总负荷的15%。
PiDG≤15 kW
(10)
PiDG≤30%PIL
(11)
(12)
式中PiDG为i节点接入屋顶光伏的有功功率;PiL为i节点负荷功率;m为接入屋顶光伏的节点个数。
2 NSGA-Ⅱ优化算法
2.1 NSGA-Ⅱ算法原理
带精英策略的非支配排序算法(NSGA-II)采用快速非支配排序,对个体间的支配关系进行分层;采用虚拟适应度(dummy fitness)删除过于集中的个体;引入精英策略,使父代和其产生的子代共同竞争产生下一代种群[12]。
应用NSGA-II算法对多目标函数进行优化主要包括4个步骤:
(1)快速非支配排序。赋予个体i两个指标:其他个体支配个体i的数量ni;被个体i支配的其他个体的集合Si。排序过程中,把不被种群中其他个体支配的个体,即当前最优个体存入Frank,并赋予其非支配序rank,每次排序前,都需要将前次排序产生的Frank中的个体从种群中删除;
(2)虚拟适应度计算。为了稀释过于集中的个体,使得所有个体均匀地分布在Pareto前沿上,需要计算同非支配序rank下的所有个体之间的局部拥挤距离。
其计算步骤如下:
①对于边界上的个体,其拥挤距离为无穷,即Pd(0)=Pd(End)=;
②对于排序在中间的个体i,其拥挤距离计算公式为:
(13)
式中Pd(i)为解i的拥挤距离;fk(i+1)为个体i+1的第k个分目标函数值;fk(i-1)为个体i-1的第k个分目标函数值;
(3)选择运算。经过上述步骤,所有个体i都被赋予非支配序rank(i)和拥挤度Pd(i)。采用锦标赛的方式,从种群中随机选择个体,通过比较其非支配序rank和虚拟适应度Pd(i),保留较好个体,淘汰较差的个体;
(4)精英保留。将父代Pt和通过父代交叉、变异产生的子代Qt合并成一个种群Rt。按照快速非支配排序对Rt进行分级,计算Rt中所有解的拥挤距离,按照非支配序rank进行排序,同一等级按照拥挤距离Pd排序,直至选取的个数达到外部档案NS要求的数目,将选取的种群放入外部档案NS,形成新一轮进化的父代种群Pt+1,通过下一轮的交叉、变异,形成新的子代Qt+1。
2.2 改进NSGA-II算法
NSGA-II算法在二维空间里,采用拥挤距离是可以表示个体的拥挤程度,但是在三维或更高维度的空间里,常规的拥挤距离并不能很好地表示个体的拥挤程度。故文献[13]基于这一缺点,引入模拟退火算法中的Metropolis抽样对同一等级下的解的排序进行修正。本文参考文献[13]的方法,针对高维度NSGA-II算法进行改进,建立接受概率p。
(14)
式中Pd(j)为解j的拥挤距离;Pd(i)为解i的拥挤距离;T为温度。
通过虚拟适应度筛选个体的过程中,每次个体间的筛选产生一个的介于0,1之间的随机数ε,若ε小于概率p,则接受拥挤度较小的解,反之接受拥挤度较大的解。
采用Metropolis抽样来修正虚拟适应度可以优化高维度空间中解的筛选,增强算法局部搜索能力。其实现流程如图1所示。
3 模糊贴进度
多目标优化的结果是得到算法的非劣解集,最终的配置方案需要从集合中筛选出最优方案。采用模糊贴近度,通过比较各个配置方案与各单目标优化的理想配置方案的贴近距离,得到最优配置结果。
3.1 非劣解与理想解的模糊化
通过正态隶属度函数对非劣解和理想解中各分目标值的接近程度进行量化,其公式为:
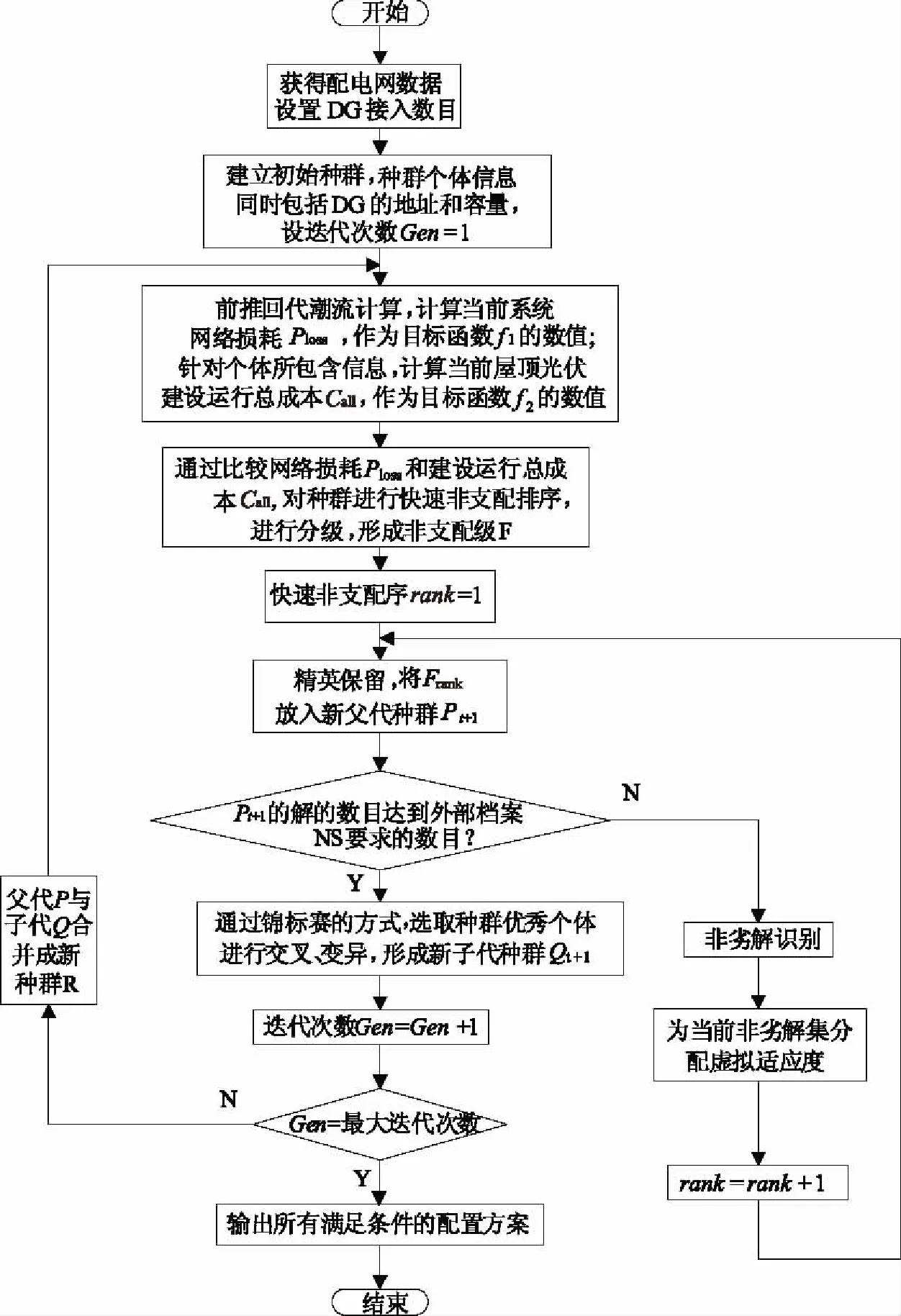
图1 改进NSGA-II算法流程图
(15)
式中k为非劣解个数;μ(frj)为第r组非劣解中的第j个目标函数隶属度输出结果;frj为第r组非劣解中的第j个目标函数值;fj*为理想解的第j个目标函数值。
其中,理想解是针对各个分目标函数进行单目标优化的结果。
将各个非劣解模糊化,以各分目标函数的隶属度为变量的建立模糊向量Fr:
Fr=[μ(fr1),μ(fr2),…,μ(frq)]
(16)
式中由隶属度含义得理想解的模糊向量为F*=[1,1,…,1]。
式中Fr为第r组非劣解的模糊向量;q是目标函数的个数;k为非劣解的个数。
3.2 模糊贴近度寻优
各非劣解模糊向量Fr和理想解模糊向量F*的贴近度可以表征两个模糊向量的接近程度,采用式(17)计算:
(17)
式中σ(Fr,F*)为第r组非劣解的模糊向量Fr与理想解的模糊向量为F*的模糊贴近度。
σ(Fr,F*)值越大,表明Fr,F*越贴近;反之,则表明Fr,F*越远离。
4 算例分析
以IEEE-33节点配电系统算例进行屋顶光伏的优化配置,如图2所示。

图2 IEEE-33节点配电系统
4.1 参数设置
在本文中,所有的屋顶光伏电站都简化为恒功率输出的PQ节点,且其功率因数恒为0.9。
屋顶光伏电进行规划时,太阳能电池板单位功率价格为3 500 元/kW,支架总成本为3 500 元/户,逆变器价格为10 000 元/户,输配设施价格为500元/户,底座成本为3 000 元/户,折现率为6.7%,周期年限为20年,维护比例K为10%,残值比例为5%。
设置节点2~33为待安装节点,选择安装屋顶光伏电站的数量为18个。
算法参数设置:种群规模pop=800,迭代次数Maxlt=400,外部档案Ns规模Scalce=70,交叉几率Pc=0.8,变异几率Pm=0.1。
4.2 理想解优化结果
采用单目标遗传算法对系统网络损耗进行优化,求取此目标函数对应的理想解f*。结果如图3所示。

图3 系统网络损耗优化结果

表1 单目标-网损优化配置方案

4.3 多目标优化结果
应用第2节针对高维度改进NSGA-II算法优化屋顶光伏电站配置结果的非劣解集在Pareto域分布如图4所示。

图4 Pareto前沿的分布情况
由分布情况可以看出,经过改进后的算法优化,非劣解均匀分布在整个Pareto前沿上,优化结果较好。并且随着投资成本的增加,屋顶光伏电站总容量增大,系统网络损耗不断降低,符合实际情况。
4.4 模糊贴近度选择
经上述改进NSGA-II算法优化后,NO.48-NO.52组非劣解见表2,可见各个解是半有序的,无法比较优劣。现用文中的模糊贴近度进行分析。

表2 Pareto解集中N0.44-48组非劣解
采用式(9)来计算各组非劣解对应的隶属度,形成模糊向量结果见表3。

表3 N0.44-48组模糊向量
采用式(12)计算各组模糊向量与理想解的贴近度,结果见表4。

表4 N0.44-48组模糊贴近度
经改进NSGA-II算法优化后,产生了70组非劣解,按上述步骤对70组非劣解的模糊贴近度进行计算。结果为第46组非劣解最优。因此最优解为:
F46=[178 0432,175.882]
此种情况下对应的屋顶光伏配置见表5。

表5 最终配置方案
按此配置方案在IEEE-33节点系统中接入屋顶光伏,相对于未接入屋顶光伏电站的系统,在保证经济性的同时,局部电压水平得到改善,发挥了屋顶光伏电站对改善供电质量的作用,如图5所示。

图5 配置屋顶光伏电站对节点电压的影响
5 结束语
针对大规模屋顶光伏电站接入农村配电网无序分布问题,首先建立了以系统网损最低和屋顶光伏电站建设运行总成本最低为目标函数的双目标优化模型,应用针对高维度解的改进NSGA-II算法进行优化,最后应用模糊贴近度的思想针对非劣解集进行筛选,得到最终配置方案。优化结果表明,文中采用的针对高维度解的改进NSGA-II算法使得种群均匀分布在整个Pareto前沿上,提高了传统NSGA-II算法的精度。优化得到的配置方案解决了屋顶光伏电站无序分布造成的分布式发电资源浪费的问题,在提高投资成本经济性的基础上,发挥了屋顶光伏电站作为分布式电源的作用,改善系统的局部电压,提高系统的供电可靠性。
