巧用三角形定则破解相对运动疑难问题
2018-12-04
(江苏省如东县马塘中学,江苏 如东 226401)
在高三力学专题复习阶段,关于求解“两根动直杆交叉点合速度大小和方向”之类的相对运动问题,是学生们感到困惑的难点。事实上,只要根据“运动合成与分解”的基本方法,找准根据、重视过程、巧妙变通,灵活运用与平行四边形定则本质一致的三角形定则,这类疑难问题就能迎刃而解。

图1
经典例题:如图1所示,在同一竖直平面内,直杆甲和乙足够长,与水平面夹角分别为α=30°、β=45°。当两杆分别以水平速度v甲=4m/s向右和v乙=6m/s向左在两杆所确定的竖直平面内平动时,求两杆交点P的速度。
方法1:应用速度分解,组合新三角形求解。
解题依据:P点实际速度vP按照平行四边形定则分解,平行四边形定则又可简化为三角形定则。对甲杆,如图2所示,vP分解为沿着甲杆向下分速度v甲1和水平向右分速度v甲。对乙杆,如图3所示,vP分解为沿着乙杆向下分速度v乙1和水平向左分速度v乙。

图2

图3
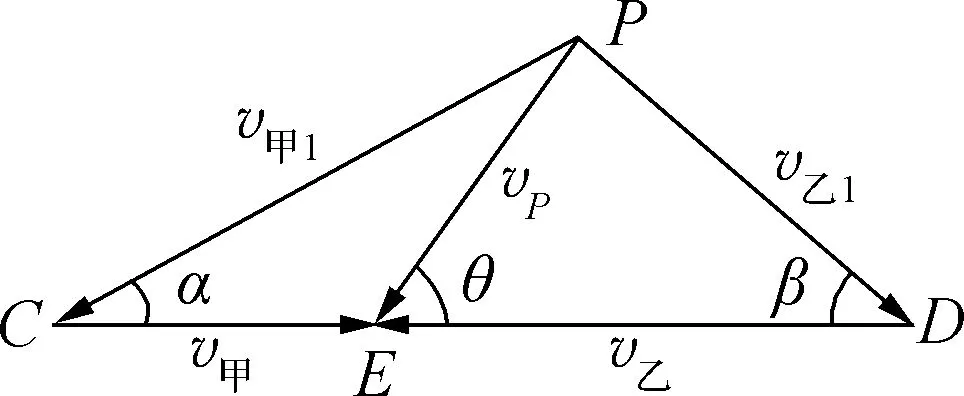
图4
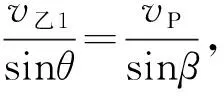
方法2:应用速度分解,构造四点共圆求解。
解题依据:如图5所示,P点速度按平行四边定法则可进行4次分解:分解为沿着甲杆方向分速度v甲1和水平向右分速度v甲,得矢量△PCE;分解为沿着乙杆方向分速度v乙1和水平向左分速度v乙,得矢量△PDE;两次正交分解得矢量直角△PAE和△PBE,它们有同一外接圆,即P、A、E、B四点共圆(圆未画出),vP为该圆直径。


图5
设图5中vP方向与甲杆夹角为α1,则v1=vPsinα1,代入数据得sinα1≈0.461,即α1≈27.5°,vP与水平方向夹角为α2=α+α1≈57.5°,两种方法结果一样。
现对上面两种解法及结果评析如下:
(1) 解题依据一致。都采用了“运动合成与分解”的思想观念,灵活运用平行四边形定则即三角形定则进行矢量运算。
(2) 求解过程推证周密。方法1中由两个矢量三角形巧妙地合二为一,在新三角形中运用余弦定理和正弦定理,通过求解三角形得解。方法2中灵活变通出两个矢量直角三角形,且有同一外接圆,用余弦定理和正弦定理推论,求解圆直径得解。求解过程都是由矢量关系图与数学定理公式相结合,数学上称“数形结合”,即物理上的“图式并用”。
变式训练:仅将前例中乙杆速度方向改为竖直向上,其他条件不变,求交点P的速度。
方法1:应用速度分解,组合新三角形求解。
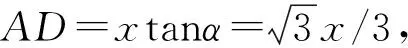

图6
方法2:应用速度分解,构造四点共圆求解。
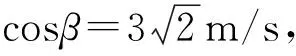

图7
