二次特征值问题中等导特征对的灵敏度分析

王平心,吴颉尔,杨习贝

(1.江苏科技大学 理学院, 镇江 212003) (2.江苏科技大学 计算机学院, 镇江 212003) (3.河北师范大学 数学与信息科学理学院, 石家庄 050024)

线性阻尼系统的自由振动方程可以表示为：

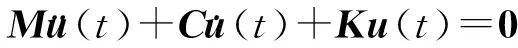
(1)

式中：M,C,K分别为质量、阻尼和刚度矩阵；u(t)为位移向量．令u(t)=ueλt(其中u是不依赖时间的常向量),代入上式则可得到如下二次特征值问题：

(λ2M+λC+K)u=0

(2)

当M,C,K均为实对称矩阵,则称问题(2)为对称二次特征值问题．如果质量、阻尼和刚度矩阵依赖于设计参量p1,p2,…,pN,则得如下二次特征值问题：

[λ2(p)M(p)+λ(p)C(p)+K(p)]u(p)=0

(3)

式中：p=(p1,…,pN)T；M(p),C(p),K(p)是在p=p0的邻域内解析的矩阵值函数．

阻尼系统的结构动力特性主要表现在其特征对上,即特征值和特征向量．因此,特征对导数的计算是理解并确定参数变化对系统影响必不可少的方法．特征灵敏度分析的主要任务之一就是计算特征对的导数,其结果在结构故障诊断[1]、结构优化设计[2]、结构分析与识别[3-4]、结构模型修正[5]和代数特征值反问题[6-7]等领域都有重要的应用．在特征对导数的计算中,特征值导数的计算比较简单,已有一些有效的方法．特征向量导数的计算需要求解系数矩阵奇异的线性方程组,是特征对导数计算中的主要难点．为了解决这一问题,许多学者在这一领域进行了大量研究,提出了多种特征对导数的计算方法[8-18]．但是,目前存在的算法大多针对特征值是单根或者特征值是重根，但特征值的导数是互异的情形．文中利用矩阵广义逆理论,推导一种计算对称二次特征问题重特征值在等导情况下特征对导数的新算法．

1 特征值的导数

假定二次特征值问题(3)在p=p0处有r重半单特征值λ0,当参数p在p0的某邻域内变化时,假设r重特征值λ0变成r个单特征值λ1(p),…,λr(p),u1(p),…,ur(p)分别是二次特征值问题(3)对应于特征值λ1(p),…,λr(p)的特征向量,并且λ1(p0)=…=λr(p0)=λ0≠λi(p0) (i>r).为便于讨论,记

Λ(p)=diag(λ1(p),…,λr(p))

U(p)=[u1(p),…,ur(p)]

由式(3),有

M(p)U(p)Λ2(p)+C(p)U(P)Λ(p)+K(p)U(p)=0

(4)

为了保证特征向量的唯一性,使用如下规范化条件：

(5)

当p=p0时,因为Λ(p0)=λ0Ir,此时规范化条件转化为：

UT(p0)(2λ0M(p0)+C(p0))U(p0)=Ir

(6)

为方便起见,如无特别声明，矩阵或向量在p=p0处取值时将p0省略,例如M(p)在p=p0处的取值M(p0)就简记为M.

考虑计算特征值的导数：

特征向量的导数：

利用求解二次特征值问题的数值方法可计算二次特征值问题(3)在p=p0处的特征值λ0和相应满足规范化条件的特征向量φ1,…,φr.记Φ=[φ1,…,φr],则Φ满足：

ΦT(2λ0M+C)Φ=Ir

(7)

注意计算所得的特征向量Φ不一定恰好是特征向量U(p)在p=p0的值U.但span(Φ)=span(U),则存在非奇异矩阵Γ,使得：

U=ΦΓ

(8)

并且Γ满足ΓTΓ=Ir.

通常在计算二次特征值问题(3)的特征向量时,几乎不可能正好找到对参数p解析的特征向量U,而只能计算Φ,再由Φ寻找矩阵Γ,从而得到U=ΦΓ.记

对式(3)两边关于pk求导并取p→p0有：

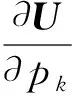
(9)

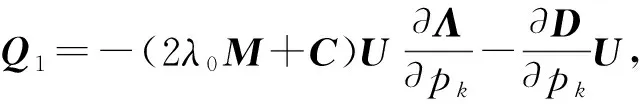
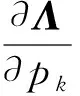
(10)

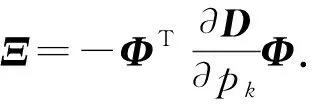
2 特征向量的导数

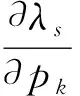
U[U1,U2,…,Uh]=ΦΓ=Φ(Γ1,Γ2,…,Γh)

(11)

Γs=ρsβs,s=1,…,h

(12)

式中，ρs满足方程：

(13)

对任意ms阶正交矩阵βs,Γs=ρss也是特征值问题 (13) 的解, 因此Γs和Us=ΦΓs不是唯一确定的．

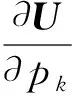
(14)

式中：G∈Cn×n为矩阵D的一个广义逆,即G满足DGD=D；α1为任意的r×r矩阵．事实上,GQ1为方程组(9)的一个特解．记H=2λ0M+C,取α1=-ΦTHGQ1,代入(13),可得方程组(9)的另一个特解,

(15)

式中，P=I-HΦΦT.由于：

则

(16)

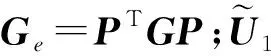
(UTH-ΓTΦTHΦΦTH)GQ1=0

(17)

因此,特征向量的导数可以表示为：

(18)

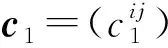
讨论如何计算系数矩阵c1.记

对式(3)两边关于pk求二阶导，并取p→p0,可得：

(19)

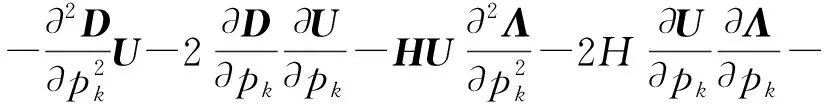
上式两边左乘UT,可得：

(20)

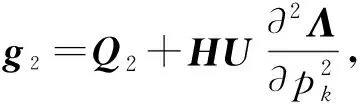
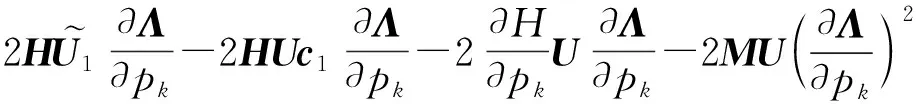
将式(16)代入式(20),并利用规范化条件(6)得

(21)

把方程(21)写成ms×mt的分块形式,可得：

(22)

式中：

在方程(21)中令s=t，并在两边左乘βs,可得：

(23)

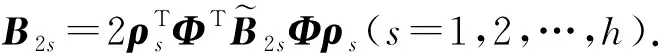
在方程(21)中取s≠t,可得矩阵c1的非对角子块：

(24)

类似于方程(3)的讨论,将式(19)的解表示为：

(25)

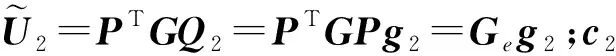
(26)

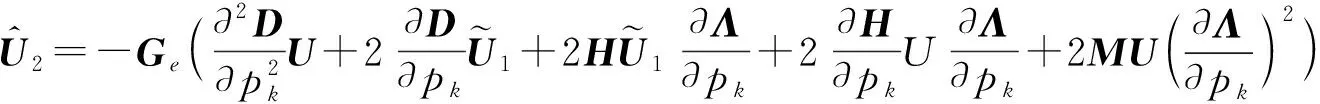
对式(3)两边关于pk求三阶导，p→p0,并利用关系(9，21，25)有：

(27)

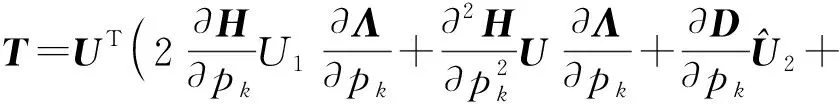
在式(27)两边取出相应的对角子块可得：

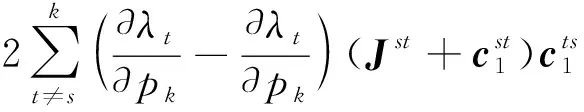
(28)

它的纯量形式为：

(29)

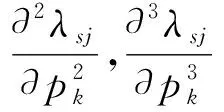
(30)

矩阵c1的对角元可由规范化条件求得．对方程(5)两边求导并令p→p0有：

(31)

将式(6，7)代入上式可得：

(32)

因此可得矩阵c1的对角元为：

(33)

通过特征向量导数的计算可以得到在特征值的导数相等的情况下特征对导数的算法．

算法: 等导情况下特征对导数的算法

输入:矩阵M，C，K以及他们关于参数的一阶、二阶、三阶偏导数，特征值λ0和相应的特征向量Φ，满足规范化条件ΦT(2λ0M+C)Φ=Ir.

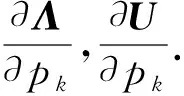
步骤：

矩阵D的广义逆G以及Ge=(I-ΦΦTH)G·(I-HΦΦT);

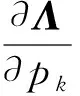
(3) 若Ξ的特征值有重根,计算

3 数值例子

考虑三自由度的弹簧质点阻尼系统(图1).

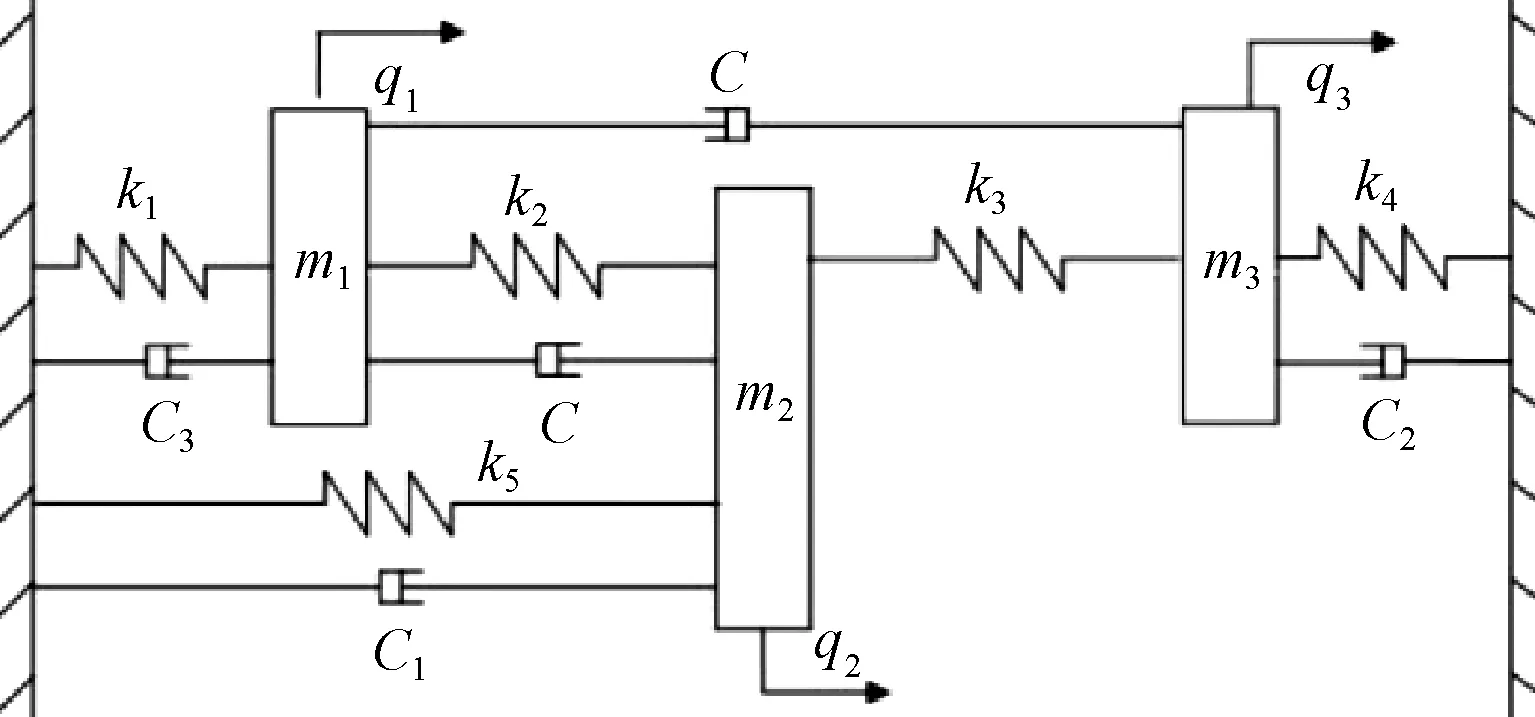
图1 弹簧-质点-阻尼系统Fig.1 Mass-damper-spring system

则系统的质量、刚度和阻尼矩阵分别为：

设参数m1=m2=m3=1 kg,

k1=k4=k5=1 000 N/m，

k2=k3=0 N/m,c1=c2=10 Ns/m,

c3=20 Ns/m.因而,

选取阻尼矩阵中的参数c为待定参数．考虑系统在c=c0=0处特征对的导数．显然,

当c=c0=0时，系统有二重特征值λ=-5-31.225i其对应的特征向量为:

利用算法1可得：

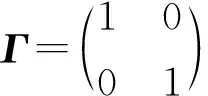
即特征值的导数有重根,而特征值二阶导数为:

由算法1得：

为了验证上述结果的正确性,设参数c的一个扰动Δc=0.1，然后计算当c=c0+Δc时系统的特征值与特征向量,并与如下近似计算结果：

比较，结果见表1、2．可见,c=c0+Δc时系统的特征值与特征向量，与近似计算的特征值与特征向量相差很小,说明文中的算法是有效的．

表1 特征值的比较Table 1 Comparison of eigenvalues

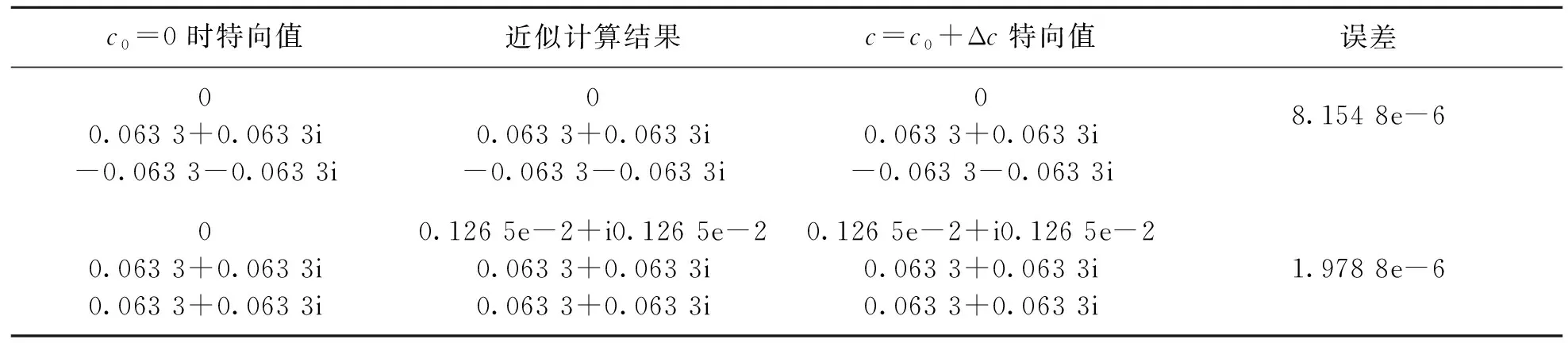
表2 特征向量的比较Table 2 Comparison of eigenvectors

4 总结

特征对导数的计算是特征灵敏度研究的主要问题．文中考虑二次特征值问题在特征值导数相等情况下特征对导数的计算问题．通过将特征向量的导数表示为一个用广义逆矩阵表示的特解和对应齐次方程组的通解之和,给出了一种计算二次特征值问题等导特征对导数的算法．该算法在n维空间中直接计算对称二次特征值问题重特征对的导数,利用广义逆矩阵导出了控制方程的一个特解,从而给出了计算重特征对导数的算法．和目前存在的算法相比,该算法可以适用于特征值导数有相等的情形,而且计算过程只需要计算系统当前特征值对应的特征对,计算量和存储量较小．

在文中研究工作的基础之上,下一步研究可从以下两方面展开:① 文中考虑了二次特征值问题特征值等导情况下特征向量一阶导数的计算,还可以考虑特征向量高阶导数的计算问题．② 非线性常微分方程特征值问题、阻尼结构系统的动力分析、流体力学中的稳定性分析、线性时滞系统的稳定性分析等领域会出现一般的非线性特征值问题,非线性特征值问题特征对的导数研究值得关注．