混合动力车用皮带驱动式分块转子开关磁阻起动/发电机的稳态热分析

周追财,孙晓东,2*,薛正旺,杨泽斌,韩守义

(1.江苏大学 汽车与交通工程学院,镇江 212013) (2.江苏大学 汽车工程研究院,镇江 212013) (3.江苏大学 电气信息与工程学院,镇江 212013)

随着能源危机、环境污染等问题的日益加剧,具有高效率、低污染等突出优点的混合动力汽车正加快其发展步伐[1-3]．作为混合动力汽车关键部件之一的发电机要求能高效、稳定地工作.不同于传统的汽车将启动机和发电机分开,皮带驱动式起动/发电一体机将启动机和发电机集于一身,取代原发电机,从而简化发动机设计,并减少车重[4-6]．目前皮带驱动起动/发电机多为混合励磁爪极电机、感应电机和永磁电机．然而对于混合励磁爪极电机,在低速时获得高转矩较难且转子结构复杂,不利于高速运行;对于感应电机,其调速性能较差,不易进行精准控制,且对电机的控制系统要求较高[7];对于永磁电机,由于存在永磁材料,所以在高温和高磁场环境下的稳定性难以保证[4,6,8,9]．开关磁阻电机以其结构简单牢固、成本低和可靠性高等优点,适用于高速运行和恶劣环境,快速成为研究热点[8]，因此文中选取开关磁阻电机为研究对象．

皮带驱动式起动/发电机的运行工况复杂,尤其在起动发动机时,要求以峰值功率在0.4 s内将发动机拖动到怠速状态[4],从而导致电机内部的温度上升,如果温度过高,不仅影响电磁参数性能,而且会破坏绕组绝缘层的,进而影响电机安全可靠的工作[10]．因此,常规的电磁参数的设计不能满足性能要求,对电机的温度场分布研究也将成为必不可少的环节．目前温度场的研究方法主要有等效热路图法、等效热网络法和有限元法[11]．有限元法是现今应用最广泛的温度场计算方法,可以详细地计算出各点温度值,而且计算精度高[12]．但通过有限元法对皮带驱动式开关磁阻起动/发电机进行温度场分布的研究还鲜有报告,因此文中采用ANSYS Workbench有限元软件对建立的三维样机模型进行温度场分析．

1 皮带驱动式SRS/G的温度场分析

1.1 电机参数

文中以一台1.8 kW的开关磁阻起动/发电机为研究对象,其三维结构如图1,定子由定子轭和定子齿组成,有8个宽齿和8个窄齿沿定子轭内圆交替分布形成定子,8个宽齿上均集中缠绕线圈,8个窄齿上则不缠绕线圈,只提供磁路的回路．相邻宽齿上绕组极性相反,相对宽齿上绕组极性相同,形成NSNSNSNS交替分布型极性,相对宽齿上的绕组反向并联成一相．另外,转子由转子铁心块和转子铝套组成,10个转子块嵌入转子铝套中,在磁路上相互隔离．转子块两端加端环,防止转子块轴向窜动．所使用的叠片材料是DW310-35,电机采自然风冷方式,具体参数见表1．

图1 16/10分块转子开关磁阻起动/发电机三维结构Fig.1 Three-dimensional structure of the 16/10 SRS/G with segmental rotors表1 SRS/G的具体参数Table 1 Specification of the SRS/G

参数数值参数数值 输出功率/W1 800定子极弧长/(°)21.375/10.69 电压/V60转子块极弧长/(°)28.08 叠长/mm80气隙长/mm0.25 定子外径/mm128定子极数/个16 转子外径/mm82转子块极数/个10

1.2 热源分布

电机内部生热主要由功率损耗造成，文中主要考虑绕组铜损和定转子的铁损,而不计及轴承摩擦等带来的机械损耗，因此将铜损和铁损作为电机生热的主要热源[12]．

1.2.1 铁损和铜损

铜损主要由流过绕组的电流引起的,可以通过路的计算方法得到,公式如下:

Pcu=mI2R

(1)

式中：m为相数,I为相电流的有效值,R为相电阻．

通过电磁场有限元软件ANSOFT自带的计算铁损工具,计算得到在峰值功率、额定功率和最高转速3种工况下的铁损分布图,如图2．图中可以看出,随着时间的增加,铁损逐渐增加,最后趋于稳定，文中取铁损稳定分布后的平均值作为该种工况下的铁损．

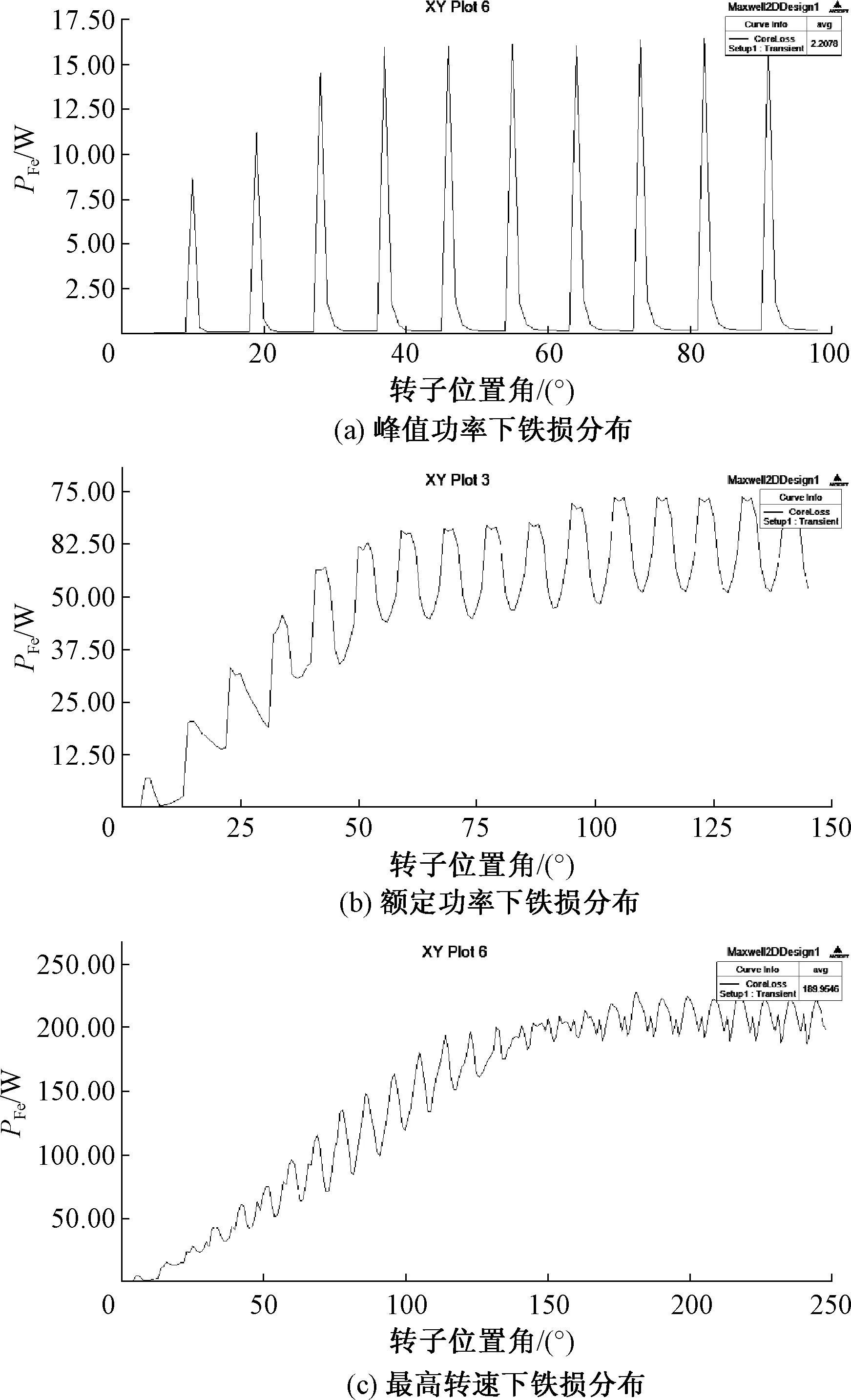
图2 不同工况下铁损分布图Fig.2 Iron losses in different working conditions

表2给出了在不同工况下铜损和铁损的具体数据值．其中,相电阻为0.03 Ω,峰值功率下的相电流的有效值为120 A,额定功率下相电流的有效值为26 A,最高转速下相电流的有效值为22 A．

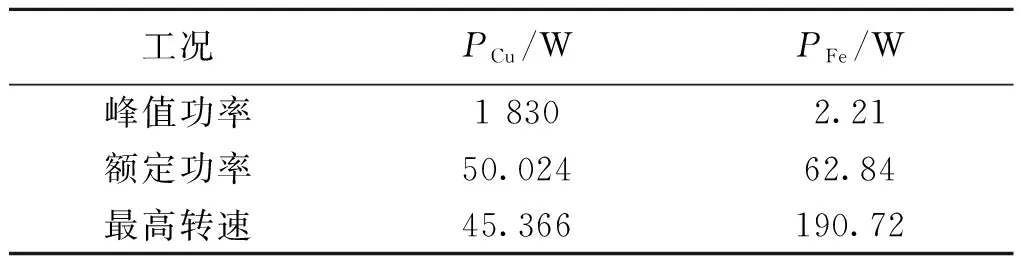
表2 不同工况下铜损与铁损Table 2 Copper and iron losses in different working conditions

1.2.2 内部生热率的计算

在获得铜损和铁损后,将其转化为内部生热率,公式如下[13]:

(2)

式中：Q为内部生热率,Pe为铜损或铁损,V为电机不同部件的体积．

对于定子铁心和转子铁心块,V就是实际的体积,但对于结构复杂的绕组,体积V可以通过如下公式近似求解:

(3)

式中：VCu为绕组铜的体积,d为导线的线径,la为定子叠长,bps2为定子宽齿的齿身宽度,N是绕组匝数,s是定子槽数．

表3给出了定转子铁心及绕组的内部生热率的具体数值．

表3 定转子铁心及绕组的内部生热率Table 3 Heat generation rates in stator/rotor cores and winding

1.2.3 导热系数

由于电机绕组的结构比较复杂,为了简化计算,对定子槽内绕组做如下假设:

(1) 忽略绕组的集肤效应;

(2) 认为电机浸渍漆良好,完全填充;

(3) 铜线的绝缘漆分布均匀．

根据以上假设,将槽内全部铜线(不包括绝缘漆)看做一个整铜块,而槽内所有绝缘材料包括铜线绝缘漆、侵渍漆、槽绝缘和槽内空气等效为另一个导热体．绕组的等效模型如图3,整铜块位于槽中间,所有绝缘材料分布在铜块四周．

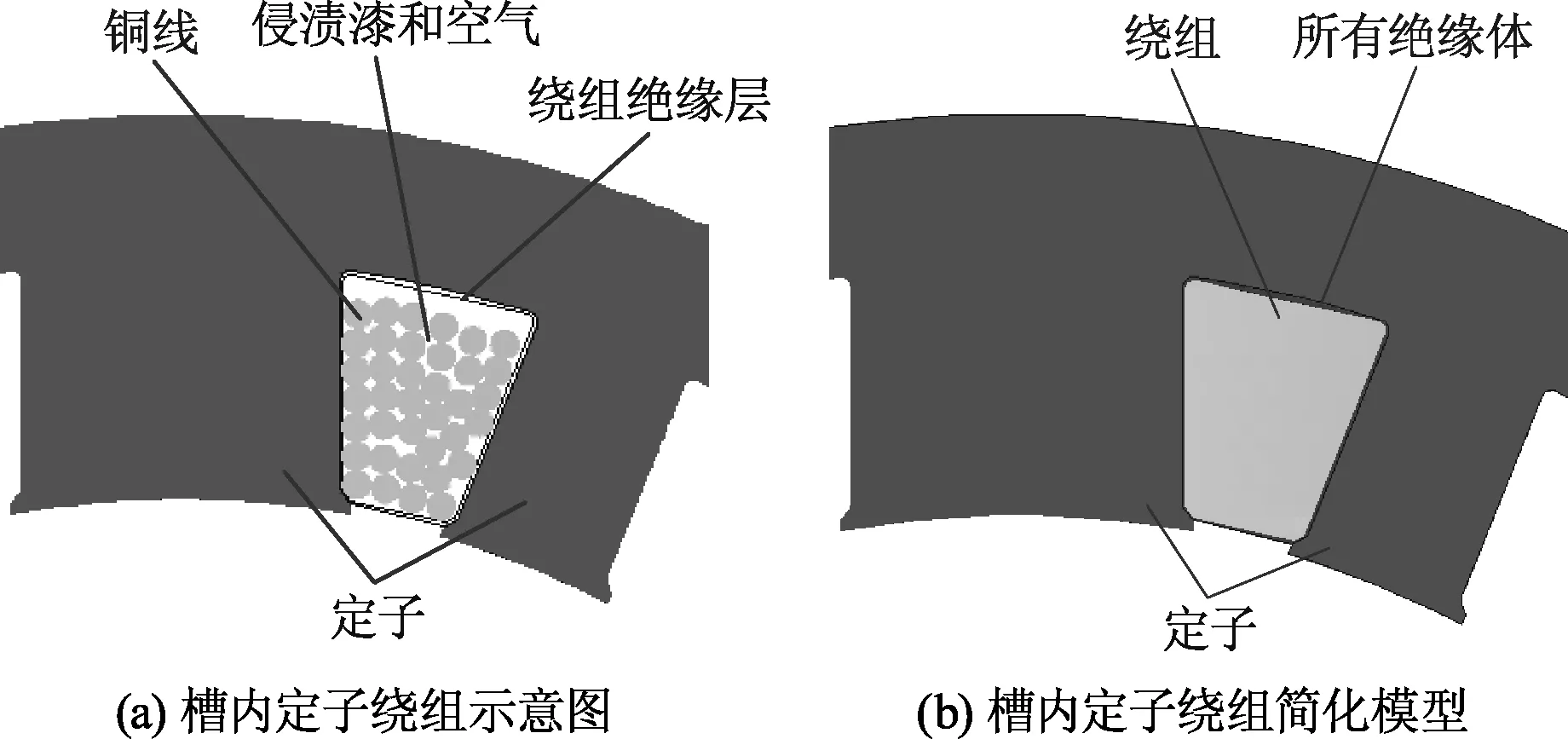
图3 等效绕组模型Fig.3 Equivalent winding model

而槽内绝缘材料的等效导热系数为[14]:

(4)

式中：λeq为导线的线芯系数；Tp为槽内导线的平均温度；d为漆包线直径；k为侵渍系数；k1为填充系数；λ为侵渍漆的导热系数,取0.18;λa为圆铜线绝缘漆的导热系数,取0.15．

表4给出了电机不同材料的导热系数．

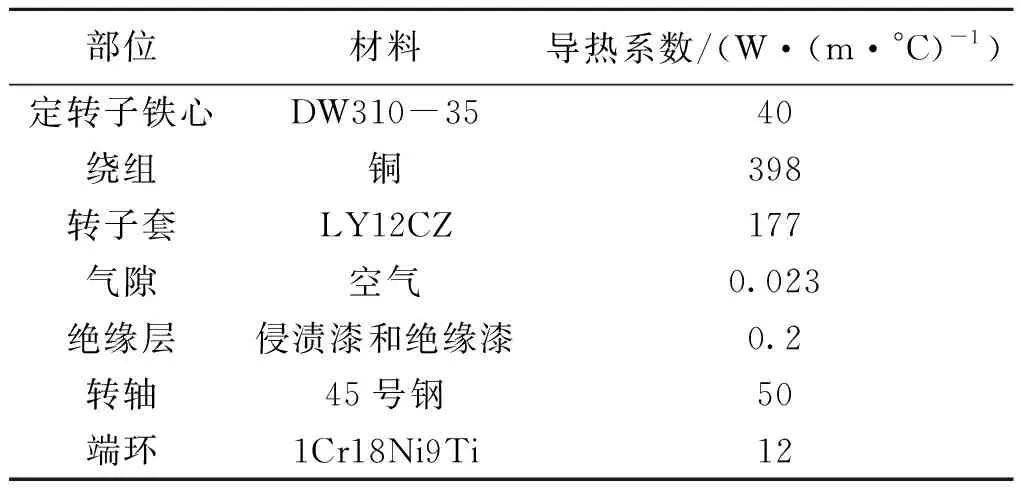
表4 电机不同部位的导热系数Table 4 Thermal conductivity factor in different parts

1.2.4 电机表面对流换热系数

对流换热系数被定义为物体表面与周围流体之间温差为1℃时,单位时间和单位面积上所交换的热量．由铜损和铁损产生的热量必须通过施加对流换热系数而传递出去．为了仿真整个模型的温度分布情况,需要在电机各表面添加对流换热系数[15]．

获取单片正射影像的过程中，应该将有关影像数据信息及时传送至相应的程序内，做好加密处理，并且依靠相应系统完成自动化匹配处理，保证DSM形成的准确性。同时，还应做好DSM的过滤处理工作，待产生相应的DEM格式以后，完成科学的影像制作处理。此外，针对影像制作的环节，运用全数字摄影测量工艺，将像片当成单位，明确具体的区间，将主点当成核心，重视相应的改进和优化，最终获得良好的单片正射影像。

(1) 气隙表面对流换热系数

气隙处的流体运动不仅受转子的切向运动的影响,而且受定子内圆表面的阻滞作用影响．定转子之间的气隙对流换热系数为：

(5)

式中：aδ1,aδ2分别为转子外表面的对流换热系数和定子内圆表面的对流换热系数；u为转子的圆周运动速度．

(2) 定子外表面向周围空气的对流换热系数

由于所研究的电机外壳采用汽车用发电机的外壳,定子外表面处于未封闭状态,因此,定子外表面的对流换热系数取为机壳向周围环境散热的对流换热系数,公式为:

(6)

式中：a为定子外表面向周围空气的对流换热系数；k为气流吹拂效率的系数,取k=0.5;v为空气吹拂外表面的速度,取自然对流风速v=0.15 m/s,θ为周围环境温度．

(3) 绕组端部、定子端部及转子端环的对流换热系数

为了模拟整个电机的温度分布情况,不仅需要考虑径向表面对流换热系数,也需要施加轴向对流换热系数,文中主要考虑了绕组端部、定子端部及转子端环的对流换热系数．由于绕组次用简化模型,所以考虑定子端部和绕组端部的对流换热系数相等,公式如下[15]:

(7)

式中：αc1和αE分别为绕组端部和定子端部的对流换热系数,k和v分别为气流吹拂效率的系数和空气吹拂外表面的速度．

转子端环的对流换热系数采用如下公式[15]:

(8)

式中：α2为转子端环的对流换热系数,u2为转子的圆周运动速度,由于不同工况下,转子转速不同,所以u2的取值也不同．

表5给出了电机在不同工况下各个表面的对流换热系数的具体数值．

表5 电机各表面对流换热系数Table 5 Convection coefficient in different parts W/m2·℃

2 仿真结果分析

在不同工况下电机的稳态温度场分析结果如图4～8．图4和图5分别表示在峰值功率下整个模型的温度分布和单个定子绕组模型的温度分布情况．

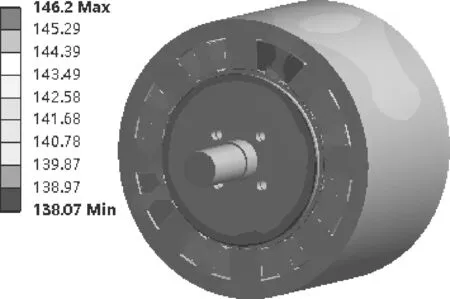
图4 峰值功率下电机整体模型温度分布情况Fig.4 Temperature distribution of the whole motor in peak power condition

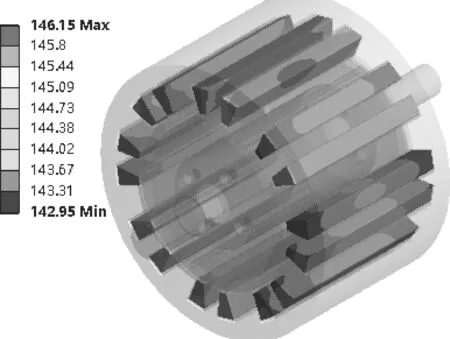
图5 峰值功率下绕组的温度分布情况Fig.5 Temperature distribution of the winding in peak power condition

从图中可以看出,在峰值功率下,最高温度出现在绕组上,达到146.2 ℃，这一数值应引起足够重视,以致于绕组绝缘材料的等级需要提高．另外,从图7中可以看出,单根绕组的温度分布情况是,中间部位温度达最高值,然后向两端延伸下降,这主要是由于绕组绝缘层导热系数低,绕组散热差导致的,同时定子槽口狭窄,使得定子损耗的热量无法及时散开．

额定功率下,电机温度分布情况如图6和图7．皮带驱动式分块转子SRS/G作为发电机运行,此时由于反电势随着电机转速的上升而增加致使电流下降,因此绕组铜损下降,此时从图7可以看出,最高温度依然出现在绕组上,达到66.251 ℃,因此,电机可以长时间稳定可靠的运行．

图6 额定功率下电机整体模型温度分布情况Fig.6 Temperature distribution of the whole motor in rated power condition

图7 额定功率下绕组温度分布情况Fig.7 Temperature distribution of the winding in rated power condition

尽管电机偶尔以最高转速运行,但考虑此工况下由于电机转速的上升,铁损上升,因此为了保证各种工况下电机都能平稳可靠工作,文中分析了最高转速下电机温度场的分布情况．图8给出了最高转速下电机模型温度分布图,从图中可以看出,由于最高转速下铁损高,导致生热率大,另外定子绕组的生热率也较高,两者所产生的热量叠加,不能及时散开,因此定转子铁心的温度达到86.223 ℃,不过可以保证此工况下电机的安全可靠工作．

图8 最高转速下电机整体模型温度分布情况Fig.8 Temperature distribution of the whole motor in maximum speed condition

3 结论

文中提出了一种混合动力车用皮带驱动式分块转子开关磁阻起动/发电机,为了验证其能安全可靠的运行,分析了电机的稳态温度场分布情况．首先介绍了绕组的等效导热系数及电机各部件的表面对流换热系数,再利用电磁场有限元软件ANSOFT,计算电机定转子铁损以及绕组铜损,然后将其转化为生热率加载到ANSYS Workbench 的稳态热分析模块中来仿真分析此电机在峰值功率、额定功率和最高转速等3种不同工况下的稳态温度分布情况，最后仿真研究结果表明:

(1) 电机在峰值功率下刚起动发动机时温度最高,然后随着电机转速的上升,温度下降到一个合理的范围.

(2) 电机可长时间可靠安全的运行,但仿真结论有待后续实验验证.

(3) 当电机以最高转速运行时,电机可以安全可靠地正常工作．

文中研究对检测电机及绕组的可靠工作起了有益作用．