抗冲瓦结构在脉冲载荷下的动态响应分析与优化

陈嘉伟,张 辉,侯小军,倪其军

(1.武汉理工大学 交通学院,武汉 430063) (2.中国船舶科学研究中心,无锡 214082)

现代海战中水面舰船在海上执行作战任务时不可避免会遭受到距舰船一定距离的鱼雷、水雷和深水炸弹等水下武器的攻击．文献[1]中研究了舷侧多舱防护结构的抗冲击性能，文献[2]中对4种型式的新型双层舱壁结构响应进行数值仿真计算,并获得了抗爆性能较优的夹芯双层舱壁．而敷设抗冲瓦结构的舰船能有效降低舰体结构的冲击输入载荷[3-6],改善舰船的整体冲击环境,提高舰船的生命力．抗冲瓦结构通常敷设在整个舰艇水线以下外板表面,采用橡胶味基材,芯层具有较大的空腔,上下表面是硬度较高的橡胶板,具有夹层板的典型特征．其在受到冲击后利用变形吸能效应消耗爆炸能量,并在冲击后自动恢复原状．根据现有的研究表明,芯层结构的不同对抗冲瓦的抗冲击性能具有一定的影响[6],手征拓扑结构具有很好的力学性能[7-11],其概念来自于分子结构,将手征结构应用于抗冲瓦芯层后其抗冲击性能得到很大的提高．但目前国内关于抗冲瓦结构的研究较少,文中主要对抗冲瓦结构在脉冲载荷下的动态响应进行分析,对其变形吸能机理进行分析,研究其胞元结构对其抗冲击性能的影响,并基于多学科优化软件Modelcenter,应用遗传算法对其进行动态载荷下的抗冲击性能优化．

1 计算模型

抗冲瓦结构模型如图1,由上下两层4 mm的面板和中间手征夹芯层组成．模型初始长m=80.8 mm,高n=53 mm,水平方向两圆之间的距离g=10.39 mm,竖直方向两圆之间的距离h=18 mm,水平方向两圆之间的距离g=0.577 3×h．圆的半径r=2 mm,三角形为等边三角形,初始边长为3.47 mm,s为在此三角形基础上放大或缩小的倍数．文中基于py语言对其建立参数化模型,在以后的分析中,通过直接改变变量的取值就可得到所需模型,从而避免重复建模的麻烦．文中所研究的问题属于浅水爆炸问题,所以不考虑静水压力的影响,爆炸载荷仅考虑冲击波载荷,因此采用脉冲载荷的方式进行加载[6]．在模型的上表面(y方向)施加一个三角形脉冲载荷,取脉冲载荷的时间t为0.02 ms,峰值大小为15 MPa．手征结构的下表面与钢板通过tie连接,其x和z方向采用对称边界条件,钢板的四周固支．在受到高应变率载荷时,橡胶的动力学分析一般都采用粘超弹性本构关系,所取粘弹性为基于Prony级数的本构模型,超弹性模型为Arruda-Boyce,具体参数设置如表1[6]．文中探讨的是抗冲瓦结构的抗冲击性能的优化,故取钢板中点的加速度峰值为目标值，计算时间取5 ms．各测点布置如图1,从上至下依次为A1、A2、A3、A4．

图1 抗冲瓦模型Fig.1 Model of anti-shock chiral layer表1 材料参数Table 1 Material parameters

钢板橡胶拉伸弹性模量E/Pa泊松比v初始剪切模量μ/Pa锁死应变λm剪切松弛的模量比gP1体积松弛的模量比τG12.1×10110.3976 591.72.7030.40.1

2 结果分析

2.1 变形分析

抗冲瓦芯层结构在脉冲载荷下的变形模式主要包括冲击端变形、孔的屈曲和压溃、固定端的变形、整体回弹4个阶段．图2～4中，当r=2.0 mm,s=1.5,h=18 mm时在不同脉冲载荷下(峰值依次为15、25、35 Mpa)的变形图．当载荷峰值为15 MPa时,图2中：当t=0.120 ms时,结构冲击端受到冲击后出现了局部的压缩大变形,但孔洞并没有完全被压缩密实．随后在应力波向上传播的过程中,芯层的单胞结构利用手征拓扑结构自身发生旋转的性质以及孔洞的压缩来吸收能量,达到了局部变形大而整体变形小的效果,展现了其负泊松比性质的优越性．在芯层压缩的过程中,由于手征结构的特殊性,圆形被压缩变成了朝向右下方的椭圆形,正三角形变为内凹三角形，当t=0.475 ms时,随着冲击能量的逐渐消耗,孔洞的变形程度减弱;当t=0.950 ms时结构的固支端由于应力波的反射又出现了局部压缩大变形现象,当压缩量达到最大时,抗冲瓦结构由于本身的超弹性,结构开始出现向上反弹,此后芯层开始不断重复反弹压缩的过程直至能量消耗尽．当载荷峰值为25、35 MPa时,图3、4中,由于脉冲峰值载荷的增加,抗冲瓦结构的冲击端在受到冲击后孔洞立即被完全压缩密实,随着冲击波的进一步传播,芯层的中间却没有出现内部密实现象,孔洞的变形程度也逐渐减弱．对比芯层微观孔洞结构,可以明显看出,芯层三角形孔洞比圆形孔洞更容易被压缩密实．当载荷峰值为35 MPa,t=0.775 ms时，其固定端由于应力波的反射再次出现密实状态．图5中，当r=2.0 mm、s=1.2、h=18 mm时，抗冲瓦结构在峰值载荷为25 MPa时的变形响应;图6中，当r=2.5 mm、s=1.5、h=18 mm时，抗冲瓦结构在峰值载荷为25 MPa时的变形响应．对比图3、5、6可以发现,胞元尺寸的改变对结构的变形模式影响较小,3种不同尺寸芯层结构在冲击端都出现局部密实现象,固支端出现临界密实现象,但是胞元尺寸越大,芯层结构中应力波的传递越缓慢,这是由于孔洞越大,芯层整体的屈曲对应力波的传递缓冲效果越明显．综上所述,抗冲瓦芯层结构在动态载荷下的变形主要集中在冲击端和固定端,结构的动态变形和脉冲载荷峰值的大小存在较大的关系,但胞元的几何尺寸对其影响较小．

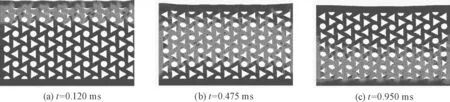
图2 峰值15 MPa下抗冲瓦结构的变形(r=2.0 mm，s=1.5，h=18 mm)Fig.2 Deformation of anti-shock layer under the impulse peak of 15 MPa

图3 峰值25 MPa下抗冲瓦结构的变形(r=2.0 mm，s=1.5，h=18 mm)Fig.3 Deformation of anti-shock layer under the impulse peak of 25 MPa

图4 峰值35 MPa下抗冲瓦结构的变形(r=2.0 mm，s=1.5，h=18 mm)Fig.4 Deformation of anti-shock layer under the impulse peak of 35 MPa

图5 峰值25 MPa下抗冲瓦结构的变形(r=2.0 mm，s=1.2，h=18 mm)Fig.5 Deformation of anti-shock layer under the impulse peak of 25 MPa

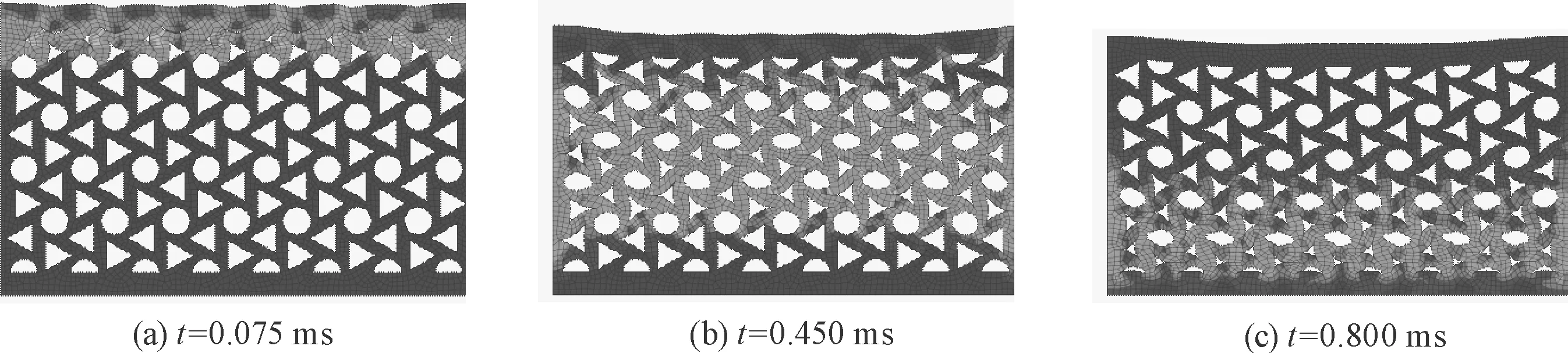
图6 峰值25 MPa下抗冲瓦结构的变形(r=2.5 mm，s=1.5，h=18 mm)Fig.6 Deformation of anti-shock layer under the impulse peak of 25 MPa

图7、8分别为抗冲瓦结构在脉冲载荷峰值25 MPa时，不同测点位置的位移D、速度v、时间t的历程曲线．从速度曲线的变化趋势来看,当受到冲击后,手征结构冲击端立即获得58 m/s的速度,在冲击传递的过程中由于能量的耗散测点A2、A3、A4的速度峰值依次为31、18、11 m/s．各测点速度的脉宽不一致,测点A2由于在冲击端,因此速度上升快，衰减也快．在随后反复的震荡过程中,各测点速度零值出现时间相同,越靠近冲击端的测点,其速度值越大．从测点的位移曲线趋势来看,各测点的最大压缩量依次为8、7.6、5.9、2 mm,可见,测点位移的峰值与间距并不是线性关系．各测点首次到达最小值时的时间不一致,越接近固定端的测点，到达时间越快,这是由于橡胶材料具有粘滞性．

图7 测点时间位移Fig.7 Curves of displacement-time

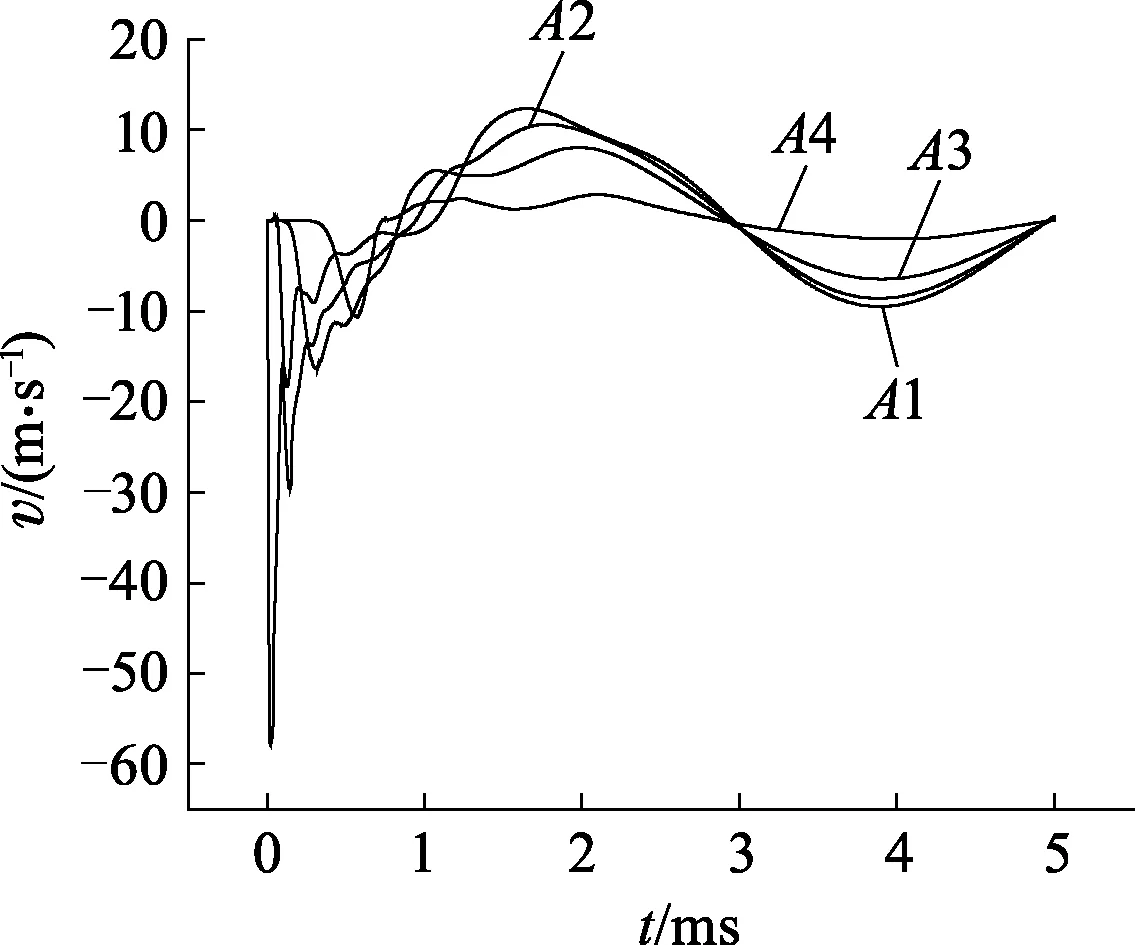
图8 测点时间速度Fig.8 Curves of velocity-time

2.2 抗冲击性能分析

敷设抗冲瓦结构主要用于降低舰船所承受的冲击环境,因此以测点加速度为主要分析对象,并且后续的优化也是以加速度峰值为目标进行展开．

图9为各变量与结构抗冲击性能的关系曲线,文中直接利用Modelcenter软件基于前文建立的全参数化模型，通过参数分析功能拟合获得,在计算的过程中,只须输入变量的取值范围及计算次数,如表2,提高了计算效率．纵坐标为钢板中点的最大加速度a．在计算变量r的敏度时,h、s保持初始不变,其他变量与此类似,载荷峰值取为15 MPa,边界条件与前文一致．

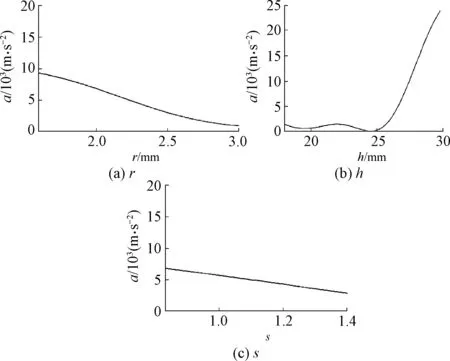
图9 结构尺寸与抗冲击性能的关系Fig.9 Relationship between geometry and shock resistance

从图9中可以看出：随着变量s、r增大,结构的抗冲击性能也随之提高,且基本成线形关系,可见孔隙率的增大有利于抗冲瓦结构的吸能,提高抗冲击性能，随着h的增大,结构的抗冲击性能大体上呈现减弱的趋势．因此胞元几何尺寸对其抗冲击性能有较大影响．

表2 变量取值范围与计算次数Table 2 Range of design variable and calculating times

2.3 优化分析与结果

根据前文可知手征结构的几何尺寸对其抗冲击性能的影响，主要应用Modelcenter软件对抗冲瓦结构进行优化,该方法的具体步骤:

(1) 根据优化设计要求确定优化设计变量、优化目标和约束条件．对于抗冲瓦结构,结构的几何尺寸r、h、s定为设计变量,抗冲瓦在5 m深静水压强的作用下的压缩比(压缩的最大值与结构原来高度的比值)不能超过0.08定为约束条件,钢板中点的加速度峰值最小定为优化目标．变量的取值范围如表2．

(2) 鉴于Modelcenter对软件的集成需要3个文件,即输入文件、执行文件、结果文件．根据(1)中要求建好全参数化模型py文件(输入文件)、执行文件、结果文件．其中py文件有2个,一个用来计算手征结构在静水压强下的压缩比,另一个用来计算抗冲瓦结构的目标值(加速度峰值)．

(3) 利用Modelcenter软件集成(2)中的py文件、执行文件、结果文件,优化界面如图10．

(4) 选择遗传算法对目标函数进行优化,计算流程如图11．

图10 优化界面Fig.10 Optimizing interface in modelcenter

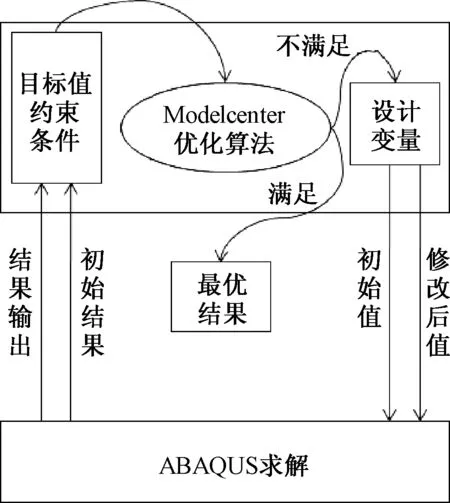
图11 计算流程示意Fig.11 Schematic diagram of optimizing process

图12为优化过程中变量的取值,点表示的是目标函数值．在优化的过程中,变量的随机取值可能造成结构的奇异性,因此出现了圈中不合理的结果．文中优化一共进行了148次迭代．图13为变量Pareto图,所谓Pareto图是基于根据计算得到的结果,将变量按照对给定响应的贡献排列,即变量的影响因子排列．图中横坐标为变量的影响因子所占的百分比．可以发现,变量h的影响因子最大,即对结构抗冲击性能的影响最大,其次是变量r、s．Pareto图不仅能分析各个变量对目标函数值的影响,同时还能计算出变量之间的关系对目标函数值的影响．从图中可以看出,h和r的比值对目标函数值的影响较大,所占的比例分别为0.13．其次是h和s的比值以及r和s的比值．Pareto图中的最后一项higher order effects指的是2个以上变量之间的关系对其结果的影响因子．

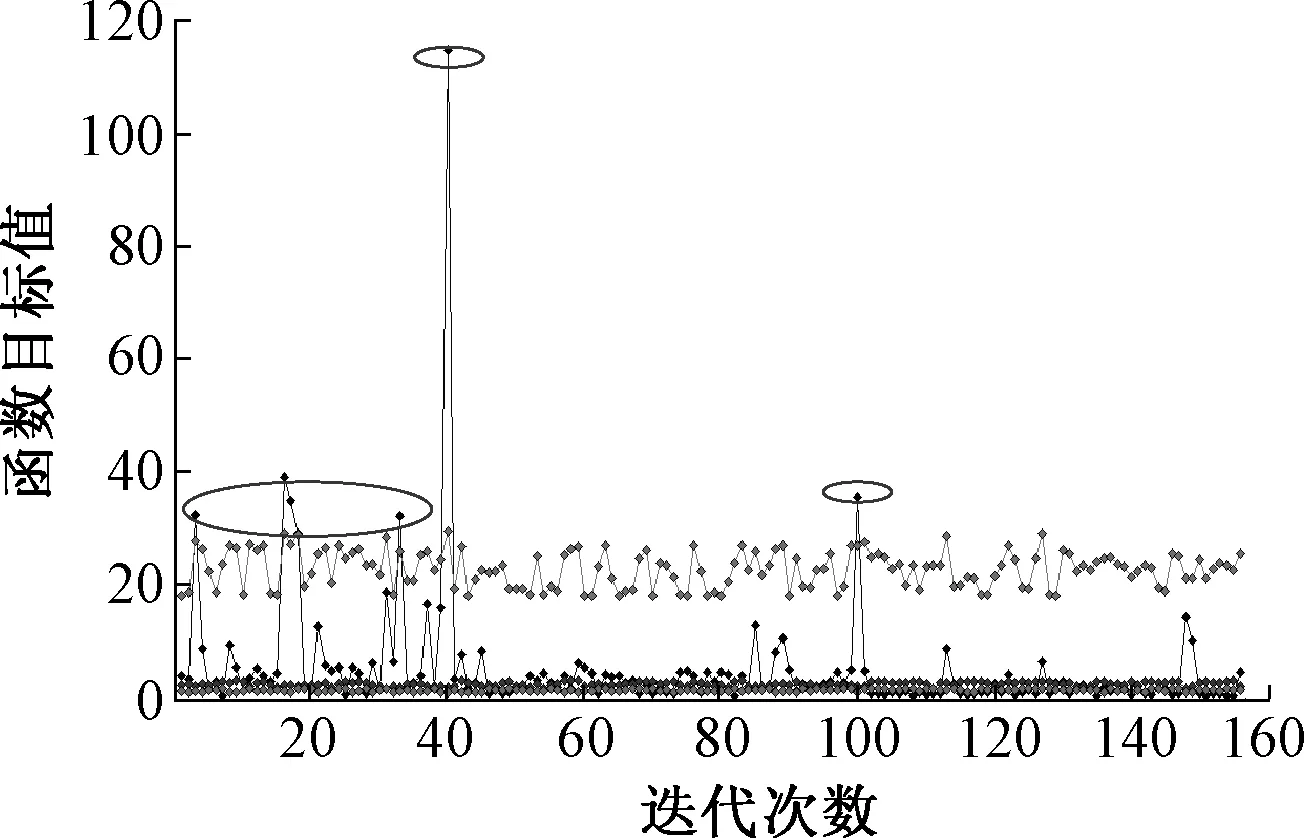
图12 优化过程Fig.12 Optimizing process

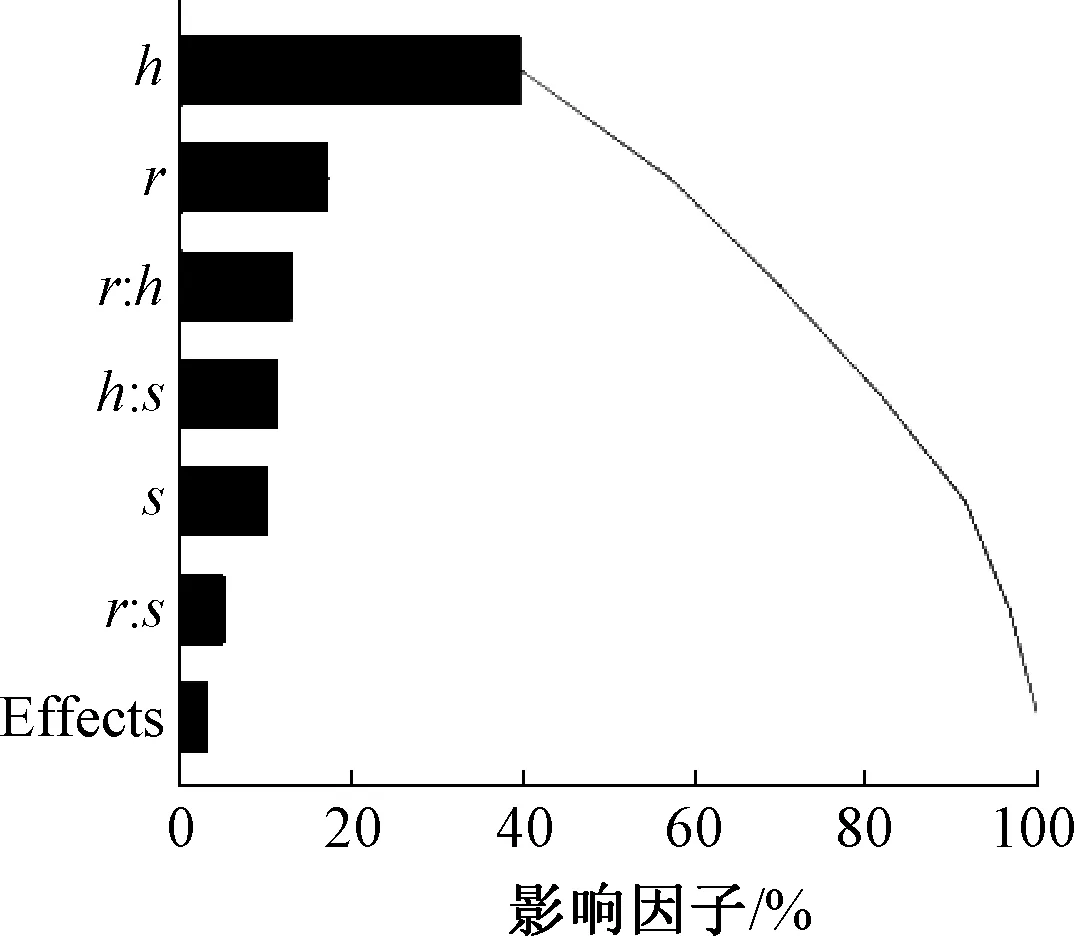
图13 变量ParetoFig.13 Variable of pareto

表3为是抗冲瓦结构在不同载荷优化的结果,当峰值载荷为15MPa时,相比优化前的目标函数值,优化后的目标函数值a降低了40.5%．可见,通过优化,结构的抗冲击性能有了较大的提高．

表3 优化前后模型尺寸的对比Table 3 Anti-shock layer geometry comparisom before and after optimizing

3 结论

(1) 抗冲瓦结构受到动态载荷后,在冲击端和固定端出现压缩大变形,当峰值载荷为25、35 MPa时,冲击端和固定端会进入密实阶段．

(2) 抗冲瓦结构的抗冲击性能与胞元的几何尺寸有很大的关系,其抗冲击性能与胞元体中圆半径r和三角形放大倍数s成正比关系,而随着竖直方向两圆之间的距离h的增加,结构的抗冲击性能总体趋势上会减弱．

(3) 基于多学科优化软件Modelcenter,结合py参数化设计与遗传算法,并利用Abaqus进行评估的优化路线,可以实现抗冲瓦胞元在动态载荷下的优化,结果表明结构的抗冲击性能有了较大的提高．