中、新初中数学教材中“三角形”的比较研究

常 艳，朱 哲

（浙江师范大学教师教育学院）

教材是课程标准的具体体现，同时也与师生教学活动的进行紧密相连.好的教材人人需要.近年来，我国的数学教育在不断变革和完善.为了更好地顺应时代的发展，实现教育目标，教材的设计与编写也应与时俱进.

本文选取了备受多国欢迎的新加坡初中数学教材，将其与我国的数学教材进行比较，从不同方面寻求两国教材编写的差异，希望能获得我国教材编写的相关启示和建议.

一、研究的背景和对象

对于初中生来说，“三角形”这一概念在印象中只是一个简单的几何图形，学生对它的具体特征及性质并不清楚.能否在学习这一章节时掌握三角形的基础知识，学习解决几何问题的基本方法，发展相应的数学能力，影响着学生接下来对平面几何和立体几何的学习，因此，“三角形”这一章节的学习至关重要.而教材对本章的编排又潜移默化地影响着学生的学习效果.

近年来，新加坡学生在TIMSS和PISA这两个国际著名的学业水平测试中表现优异，反映出新加坡数学教育的高水平.因而新加坡的数学教材也受到了美国、英国等多个国家的认同，并在部分地区使用改编后的新加坡数学教材.研究报告也表明，使用新加坡数学教材后学生的学业水平与使用当地教材的学生相比确有提高.这进一步证明了新加坡数学教材的优越性.为学习新加坡的教育特色，我们以初中数学教材为基点，选取两国教材中内容相同的章节——“三角形”，进行多方面的比较和剖析.

本文研究的具体对象为：（1）人教版《义务教育教科书·数学》（以下统称“人教版教材”）第11章“三角形”；（2）新加坡数学教材《New Syllabus Mathematics》第11章“三角形、四边形和多边形”.

二、研究方法和内容

本文主要采用文本分析法和定量分析法研究两个版本初中数学教材的异同.虽然研究的对象不是整本教材，但是通过对两个版本的教材中某些共有部分的深入研究，也能得到具有一定代表性的结论和启示.本文主要从章节结构、知识呈现方式和习题设置三方面对其进行比较研究.

1.章节结构

《义务教育数学课程标准（2011年版）》在教材编写的建议中指出，教材的编写应体现知识的整体性和过程性.这里的整体性和过程性不仅指整本或整套教材，也包括章节内部的整体性和过程性.而章节的知识结构是本章知识的浓缩，最能体现教材编排的特点.

图1是对两个版本的教材的章节知识结构图的比较（图1是人教版教材第11章知识结构图，图2是《New Syllabus Mathematics》第11章知识结构图）.可以看出，两个版本的教材所选取的内容大致相同，但是学习的侧重点和知识结构有较大差异.

图1

图2

人教版教材本章标题为“三角形”，内容有三角形及其性质、多边形及其性质，并侧重于前者.对于后者的学习，主要是让学生在重点掌握三角形及其性质的基础上，用研究三角形的方法类比出多边形的一些性质.这也意味着三角形的学习既重基础知识的掌握，又重视对它的深入学习和运用.而多边形的内容所占篇幅较少，只对基础知识（多边形的定义、多边形的内角和及外角和）做了介绍，对它们的深入学习（如平行四边形）则放在了九年级教材上.

《New Syllabus Mathematics》的章节标题为“三角形、四边形和多边形”，内容有三角形及其性质、四边形及特殊四边形性质和多边形及其性质.这一章节并没有重点、非重点之分，每一节选取的知识都较基础.例如，在第1小节三角形的学习中并没有涉及三角形的中线、角平分线和垂心的概念，第2小节的主要内容是四边形内角和和特殊四边形（矩形、正方形、平行四边形、菱形、梯形和风筝形）的学习，而第3小节是多边形及相关定理的学习.可以看出，《New Syllabus Mathematics》所选取的内容相对较广，注重学生对基础知识的学习和掌握，难度不大.

总体而言，人教版教材和《New Syllabus Mathe⁃matics》在本章的编排中都具有较强的系统性和逻辑性，各有侧重.人教版教材侧重学生对知识的系统学习和深入学习，体现了知识选取的螺旋型与直线型相结合的原则；《New Syllabus Mathematics》则重视基础知识的掌握和知识的全面学习.

2.知识呈现方式

三维目标中的“过程与方法”如何有效落实？其中一个重要环节就是教材中知识的呈现方式.我们都知道，任何数学知识都不是凭空产生的，都有其发生、发展的历史过程.若教材的编写忽视了知识产生的过程，只注重对结果的理解和运用，那么学生的思维能力和数学素养又将如何提升呢？因此，教材中知识的呈现方式关乎学生未来的发展.

笔者对两个版本教材中知识的呈现方式做了简单的对比，并从知识的引入、知识的学习流程和知识的总结三方面进行简要分析，具体情况如表1所示.

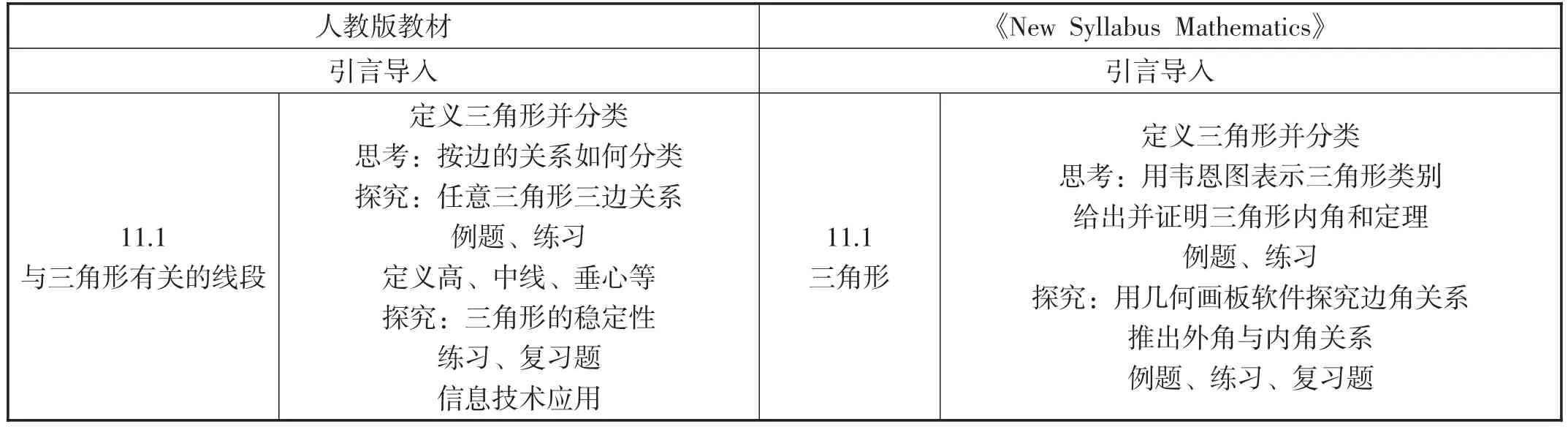
表1：“三角形”知识点学习流程比较

续表

（1）知识的引入.

在新知识的引入过程中，人教版教材选用了一幅现实生活中常见的建筑物为背景图（该建筑物采用三角形结构建成），并通过章前语很自然地引入新课题.例如，“三角形是一种基本的几何图形，从古埃及的金字塔到现代的建筑物，从巨大的钢架桥到微小的分子结构，到处都有三角形的形象.为什么在工程建筑、机械制造中经常采用三角形的结构呢？”从学生的生活背景出发引出三角形，进一步发问“三个角之间有什么关系？三条边之间有什么关系？”最后大致叙述本章的学习过程.如此的设计很有必要，把数学与现实世界相联系，引发学生学习的兴趣，激发学生探索的欲望.

《New Syllabus Mathematics》中的章前语分为两部分，第一部分直接列出本章学习目标，第二部分则通过生活中的多边形例子导入.举例如下.

学习目标：

在本章学习之后，你应该能够做到：

识别不同形状的三角形、特殊四边形及多边形，并陈述它们的特性；

解决与三角形、特殊四边形及多边形性质相关的问题.

准晶体是一种建筑材料，在很多的金属合金中能找到它.多边的准晶体有8个、10个或12个对称面.它们分别是八次对称准晶、十次对称准晶和十二次对称准晶.

可以看出，两个版本的教材在新知识的引用上，都注重从现实背景引入新知.《New Syllabus Mathematics》中还列出了本章学习目标，在一定程度上为学生指明了本章的学习方向，有利于学生把握重点，可以减少学生学习的盲目性.

（2）知识的学习流程.

①在知识的学习流程中，两个版本的教材大体相同，但又有差异.

人教版教材的知识呈现方式是给出定义、提出思考问题、探究，并得出结论、例题、复习题.其中对于直观的数学术语（如三角形、高、中线、垂心）采用直接下定义的方式给出；对于重要的定理（如三角形的内角和为180°）则采用思考或探究的方法提出问题、文字推理、证明步骤、得出结论.

《New Syllabus Mathematics》的知识呈现方式是给出定义、绘制表格、思考、探究、课堂讨论、例题、复习题.

②两个版本的教材有较大区别的是思考和探究部分.

在“思考”部分，与《New Syllabus Mathematics》相比，人教版教材中的思考问题较为简单，问题的数量也较少.并且问题提出以后具体的思路和答案已经写在了教材上.而《New Syllabus Mathematics》中并未给出具体答案.

在“探究”部分，两个版本的教材中的探究多用于定理的推导和证明.人教版教材的探究形式多是书面上的推理性的探究，即文字推理的方式，运用先前的结论推理出新的结论.这样的探究方式体现了教材对逻辑推理的重视.《New Syllabus Mathematics》中的探究多是问题式的探究或操作式的探究，即通过一系列的问题或具体的实验操作引导学生得出结论.例如，在探究几何图形的特性上，一般是借助于几何画板软件，逐步推演出定理.在推演的过程中，设计了一系列的问题做引导，可见《New Syllabus Mathematics》更重视学生的实际操作能力和思考能力.

相对来说，人教版教材在知识呈现上更重视以逻辑推理的方式呈现新知，而《New Syllabus Mathematics》更注重体现过程性，重视学生对知识发现和探究的过程.“三角形”这一章属于平面几何，因此，这一章的一些定理是可以借助几何画板软件进行探究的，让学生在实际的操作中发现并解决问题，进而获取新知.

《New Syllabus Mathematics》中几何画板软件被使用了三次，并分别证明了定理：大边对大角，小边对小角；任意两边和大于第三边；四边形的内角和为360°.

下面呈现两个版本教材的共有部分——“三角形的两边之和大于第三边”的具体例子，以此来说明两个版本的教材编写的异同.

人教版教材.

探究：任意画一个△ABC，从点B出发，沿三角形的边到点C，有几条线路可以选择？各条线路的长有什么关系？能证明你的结论吗？

对于任意一个△ABC，如果把其中任意两个顶点（如B，C）看成定点，由“两点之间，线段最短”，可得AB+AC>BC.①

同理，有AC+BC>AB，②

一般地，我们有三角形两边的和大于第三边.

由不等式②③移项，可得BC>AB-AC，BC>AC-AB.这就是说，三角形两边的差小于第三边.

《New Syllabus Mathematics》.

探究：利用几何画板软件做出一个任意三角形.

如图3展示了一个三角形，它由3个角及其对边构成.若∠A的对边为a，命名∠B的对边和∠C的对边.

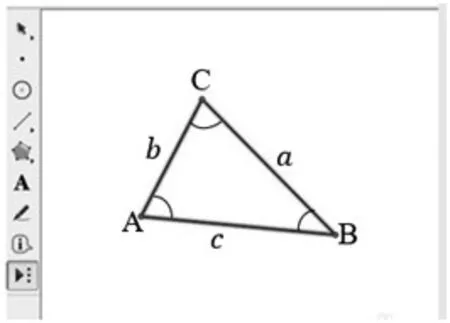
图3

1.指出最大的角和最小的角.比较这些角的对边的长度，你有什么发现？

2.移动点A，B，C中的任一点来改变三角形的形状.观察此三角形的任意一角和它对边的关系，你能得到什么结论？

3.用计算器比较三角形的最长边与另外两边之和的大小关系，你得出了什么？

4.重复第3步，你的第4步获得的结论还成立吗？解释你的答案.

5.给出三条线段a=5 cm，b=2 cm，c=9 cm.观察得到两个较短的边长之和小于最长的边长.请移动线段的两个端点，看是否可以构成一个三角形.

6.调整a，b的长度使a=3 cm，b=4 cm.调整c的长度使c=7 cm.比较a+b和c的大小，试着构造一个三角形.

7.改变这三条线段的长度.你能构造一个三角形吗？三角形的任意两边之和与第三边的长度有什么关系？

得出关于三角形边角关系的两条结论.

同样的知识内容，两个版本的教材却有截然不同的呈现方式.虽然都采用了探究的方法，但人教版教材中的探究过程更多的是推理，通过之前的定理“两点之间，线段最短”直接推出了“两边之和大于第三边”的结论.而《New Syllabus Mathematics》中的探究过程更多的是观察与思考，通过一系列的问题引导学生的实际操作，让学生在操作中总结出“两边之和大于第三边”的结论.

（3）知识的总结.

在知识总结方面，人教版教材的小结出现整章内容学习之后，分两部分呈现.首先以简单的知识结构图的形式对所学知识做了整体整理，然后是回顾与思考，总结研究多边形的基本方法，并提出5个问题引导学生回顾本章知识.

《New Syllabus Mathematics》的总结也出现在整章内容的学习之后，主要以陈述句的形式总结本章的重点内容及定理.

1.三角形的内角和是180°.

2.三角形的一个外角等于与它不相邻的两个内角之和.

3.一个四边形是一个有四条边的封闭图形.

四边形的内角和是360°；

矩形的对角线互相平分且长度相等；

正方形的对角线互相平分且相等，它们的夹角为90°，并且平分正方形的内角；

平行四边形的对角线互相平分；

菱形的对角线互相平分且夹角为90°，并且平分菱形的内角；

风筝形的两条对角线夹角为90°，其中一条平分风筝形的内角.

4.多边形的内角与其相应的外角的和是180°.

5.一个n边形的内角和等于( )n-2 ×180°.

6.一个n边形的外角和等于360°.

从上述对比可知，人教版教材中的总结主要是对本章学习流程的总结，为学生理清本章学习思路.最后以提问的方式概括学习要点，给学生留下思考的空间.而《New Syllabus Mathematics》的总结是对本章所学习的重点公式、定理的总结，与本章开头的学习目标相照应，更利于学生把握学习方向.

3.习题设置

习题的设置不仅用来测试学生掌握知识的情况，更重要的是帮助学生巩固知识、理解知识.好的教材也应该具备一套合理的、能有效帮助学生学习的习题体系（本文所指习题包含了教材中的例题、练习、复习题和总复习题.其中练习是在小节知识未结束时出现的，而复习题是在小节知识结束后出现的，总复习题是在本章知识结束后出现的）.观察两个版本的教材，不难发现在习题的编排上，有很大的相似之处，即都采用了例题+习题+复习题+总复习题的模式.其中在复习题的编写中，都对复习题进行了分类，体现了复习题的应用价值.例如，人教版教材的复习题包含三个类别：复习巩固、综合应用、拓广探索；《New Syllabus Mathematics》的复习题包含三个层次：基础水平、中等水平、高级水平.

更进一步，笔者从两个版本的教材的习题数量和难度上进行分析探究.其中习题的难度比较主要从推理的难易程度及所涉及的知识点数来体现.

（1）习题数量比较.

分别统计两个版本的教材第11章的习题数量并将结果绘制成表2.

表2：习题数量比较

教材中的例题及练习一般是在课堂教学中完成的，复习题及总复习题一般由学生课下独立完成.通过表2中的习题数量比较可知，两个版本教材中的例题和练习数量相差不大.但是《New Syllabus Mathematics》的习题总量明显多于人教版教材，但究竟设置多少数量的习题是恰当的，是要综合考虑多个方面的，这一点还有待于我们进一步深入研究.

（2）习题难度比较.

笔者采用定量刻画与定性分析相结合的方法，并依据鲍建生教授的综合难度模型，结合本文的研究对象从中选取了推理和知识含量两个难度因素，对两个版本教材中的习题难度进行比较研究.表3是本次研究所采用的综合难度因素的水平划分.

表3：综合难度因素水平划分

在计算综合难度时，采用等级变量的自然赋值法，将每个因素的各个水平从低到高依次赋予1，2，3.并将该数作为权重.然后利用下面的计算公式（其中dij为第i个难度因素的第j个水平的权重，nij则表示这组题中属于第i个难度因素的第j个水平的题目个数），分别计算出两个版本的教材的习题在推理及知识含量上的加权平均值di如表4所示.

表4：两个版本教材习题难度因素的加权平均值

由表4可知，人教版教材的习题所涵盖的知识点数量较多，推理难度小于《New Syllabus Mathematics》中的习题.这个数据也间接反映了人教版教材更注重培养学生对知识的掌握技能，而《New Syllabus Mathemat⁃ics》更注重培养学生在解题过程中的推理能力.

三、研究的结论和启示

通过对人教版教材和《New Syllabus Mathematics》教材第11章节的比较和分析，我们获得了两个版本的教材编写上的一些差异.在章节结构上，两个版本的教材选取的内容虽很相近，但是侧重点不同.在知识的呈现方式上，人教版教材一般采用文字推理的方式呈现新知，注重学生对知识的理解和应用，《New Syllabus Mathematics》多采用问题引导和实际演示的方式呈现新知，注重学生对知识发现和探究的过程.在习题设置上，人教版教材的习题主要考查学生对知识的掌握程度和综合运用能力，而《New Syllabus Mathematics》中的习题更注重考查学生在解题过程中的推理能力.

基于上述三个方面的比较研究，我们获得了一些教材编写方面的启示.

1.明确本章学习目标

人教版教材在每一章的学习之前，都采用章前语的方式引入新知.主要是通过讲述现实情境或数学现实，在学生已有的知识体系与新知之间建立联系.而《New Syllabus Mathematics》在知识的引入上，不仅有情境引入，还直接列出了本章的学习目标，这样的编写有利于学生把握学习方向，同时也为教师的教学做了相应的指导.笔者认为，人教版教材也可以借鉴这种方式，在每章的引入部分添加本章学习目标，便于学生把握知识重难点，减少学习的盲目性.

2.知识的呈现更应该注重过程性

两个版本教材的整体结构都具有较强的整体性和逻辑性，内容的选择各有特色.但是在知识的呈现上，笔者认为人教版教材更应该注重知识的过程性.对于一些定理的学习，针对不同难度的知识，使用问题串的方式引导学生思考、发现新知，或者设计相应的数学活动，让学生亲自去发现某些定理，感悟知识的形成过程.在编写中，留出一些空白，而不是写出完整、正确的过程，这样更有利于学生理解知识的本质，同时让学生在学习的过程中发展相应的能力和素养.

3.注重现代信息技术的合理使用

现代信息技术的发展为我们的数学教育提供了便利.教学常用的信息技术软件大致有课件制作ppt、文章的编写word、网上用搜索引擎查阅资料、数学作图软件、几何画板软件或超级画板等.笔者认为，数学上对某些知识的学习可以借助现代信息技术.例如，“三角形”章节的多边形的外角和定理、函数图象的研究等.如此不仅可以吸引学生的兴趣，更有利于数学本质的揭示，进而提高教学的效率.但同时也要强调信息技术的合理使用，因为并不是所有的知识都适合用信息技术来呈现.

4.习题设置上适当加强推理难度

史宁中教授认为，数学的发展主要依赖于逻辑推理.由此可见推理能力在数学学习中的比重之大.通过对本章习题设置的比较，发现《New Syllabus Mathematics》的习题推理难度大于人教版教材.笔者认为，习题应该是学生提升推理能力的一个有效途径.因此，在习题的选取上，人教版教材还可以适当加强推理的难度，减少习题所涉及的知识点个数，让学生在做练习题的过程中，不仅能掌握所学的知识，而且能够运用相关知识进行推理，逐步地提高学生的数学推理能力.