初中学业水平考试数学命题及调控技术例析

2018-12-04高定量

中国数学教育（初中版） 2018年11期

高定量

（甘肃省基础教育课程教材中心）

初中学业水平考试，既是检测初中生是否达到各学科课程标准目标要求的重要手段，也是评价初中学校教育、教学质量的重要途径.因此，考试命题的质量，直接决定着考试评价的质量和成败.本文通过典型的初中学业水平考试数学试题，分析初中学业水平考试数学命题技术.

一、题型运用技术

初中学业水平考试数学试卷，常见的题型有选择题、填空题、解答题三种.不同的题型，因为条件、结论的数量与呈现方式不同，解题策略不同，所以考查的目标和功能也就不同，只有准确、合理地运用不同题型，才有利于考试功能的发挥.

1.选择题、填空题、解答题题型的合理使用

例1计算：

例2化简：a(a-2b)-(a-b)2.

【评析】以上两道例题，在初中学业水平考试数学试卷中很常见，它们的共同特点是所呈现的都不是它们所表征问题的最终状态——数（或式），其蕴含的问题就是要找出它们的最终表示状态，而寻找最终状态的过程又都涉及了概念理解、法则与运算律运用等，所以宜用解答题（计算题）.

如果考虑到这个问题的最终状态（数或式）具有唯一性，也可将其设计为填空题.

具体采用何种题型取决于两个方面：一是问题原型的内在结构与最终结果的特征；二是这道题目在整体试卷中考查功能的规定.

选择题和填空题都是以结果来评价学生的，不需要通过过程来评价，所以运算的量一定要小.

例3下列计算正确的是（）.

（A）x2+x4=x6（B）2x+3y=5xy

（C）(x3)2=x6（D）x6÷x3=x2

【评析】此题的考查重点是学生对运算法则的掌握情况，题目按照能否正确理解运算法则来设计备选项，涉及的法则多，且相互之间并无关联，但是解答过程和结果却有较高的关联度.这样，能正确理解运算法则的学生，可以快速得出正确的答案；没正确理解法则的学生，也难以猜测出正确答案.因此，此题的题型运用较为合理，能够有效地确保考试结果的效度.

下边的例题，题型运用就不恰当.

例4在“心系灾区”自愿捐款活动中，某班30名同学的捐款情况如表1所示.

表1

（1）问这个班级捐款总数是多少？

（2）求这30名同学捐款的平均数.

【评析】此题属于单纯的统计量计算问题，主要考查学生求平均数的熟练程度.但是如果不把“平均数”看成统计中的量，可以说此题与统计没多大关系，它并没有考查统计的本质性问题（统计推理与统计决策等），没学过统计的人也能解答此题.从此意义上讲，此题设计为解答题不合适，设计为填空题尚可.

2.选择题、填空题、解答题题型的转换

因考试功能不同的需要，有时我们需要进行选择题、填空题、解答题题型间的转换，而这种转换也是有技术和技巧的.

例5计算：2-4= ______.

例5的改编题：若某天中午的气温是2℃，到傍晚下降了4℃，则傍晚的气温是（）.

（A）4℃ （B）2℃

（C）-2℃ （D）-3℃

【评析】例5仅涉及有理数的简单运算，考查的知识单一.改编后的题目，首先赋予正数、负数实际的意义，然后将加减运算设计成一个实际的问题，4个选项的设计包含了学生对该问题的不同理解过程，这样的考查能反映出学生对问题的真正理解程度，较好地体现了学业水平考试的要求.

例6利用相似三角形的有关知识测量学校的旗杆的高度.

例6的改编题：如图1，某学习小组选一名身高为1.6 m的同学（AB）直立于旗杆（CD）影子的顶端处，其他人分为两部分，一部分同学测量该同学的影长（EB）为1.2 m，另一部分同学测量得到同一时刻旗杆影长（BD）为9 m，那么旗杆的高度是______.

图1

【评析】此题是利用相似和投影的知识测量实物的高度.利用太阳光线照射两个不同的物体所形成的投影与原物体和地面所构成的两个直角三角形相似，再借助相似三角形的性质来解决求树高或旗杆高.例6需要设计测量方案、实施方案、计算等步骤，作为解答题很合适.

如果因整体试卷的要求，上述知识的题目只能设计成非解答题，就要对它进行题型转换.改编后的题目，由于测量方案已经给出，考查的知识点较为简单，因此设计成选择题或填空题也能达到考查核心知识与技能的目的.

3.选择题、填空题、解答题题型的复合

有时，为了提高区分度，降低题目的难度，常常在解答题中复合使用选择题、填空题、解答题题型.

例7如图2，边长为2的圆内接正方形ABCD中，AC是对角线，P为边CD的中点，直线AP交圆于点E.

图2

（1）∠E的度数为_______；

（2）写出图2中现有的一对不全等的相似三角形，并说明理由；

（3）求弦DE的长.

【评析】这是解答题与填空题的复合，在不降低效度（原有知识和技能）的前提下，第（1）小题运用填空题型，降低了难度，提高了区分度.

二、效度、信度、区分度、难度和教育性调控技术

效果、信度、区分度、难度是衡量试题（卷）质量的重要指标，一道优秀的试题（卷），必须有好的效度、信度、区分度和合适的难度.效度高，不一定信度高；难度高，不一定区分度高.

教育性，也是衡量试题好坏的一个重要指标.广义的教育性，远不只试题中融入了思想品德、个性品质教育，还指融入的数学文化的教育，以及新的教育、教学理念（教法、学法）的渗透.

1.效度

效度是指考试结果的有效性和合理性，它是衡量试题（卷）考查结果是否达到既定考试目标程度的指标.其关注的核心是考什么、考到什么层次.

如例3，在选项中列出不同的运算，让学生选出哪个选项对？就比直接给出其中的某一个算式，让学生判断其运算结果是哪个选项要好，因为考查的知识、法则多，确保了考试结果的效度.

2.信度

信度是指考试结果的稳定性与可靠性，它是衡量试题（卷）是否能够稳定、一致考查学生知识水平与能力状态的指标，其关注的核心是考试结果的真实性.

在常模测量的高考中，是通过建立的公式计算来看信度高低的.初中学业水平考试是标准测量，主要通过经验把控和阅卷分析来评价信度.

例8两摞相同规格的饭碗整齐地叠放在桌面上，请根据图3中给出的数据信息，解答下列问题.

（1）求整齐叠放在桌面上的饭碗的高度y（cm）与饭碗数x（个）之间的一次函数关系式（不要求写出自变量x的取值范围）；

（2）若桌面上有12个饭碗，整齐叠放成一摞，求出它的高度.

图3

【评析】摞碗这个生活情境无论对于城市学生还是农村学生都是熟悉的，以此来构造一个富有新意的试题，在很大程度上防范了由于学生在理解问题背景（载体）上的差异而影响对其相关数学知识与能力的考查，提高了试题的信度.

例9如图4，已知AB=2，AD=4，∠DAB=90°，AD∥BC.E是射线BC上的动点（点E与点B不重合），M是线段DE的中点.

（1）设BE=x，△ABM的面积为y，求y关于x的函数解析式，并写出函数的定义域；

（2）如果以线段AB为直径的圆与以线段DE为直径的圆外切，求线段BE的长；

（3）连接BD，交线段AM于点N，如果以A，N，D为顶点的三角形与△BME相似，试求线段BE的长.

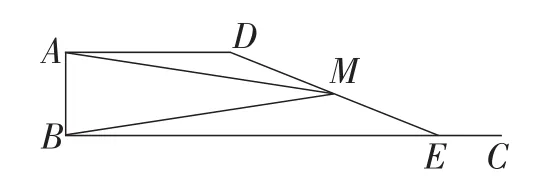
图4

【评析】这是一道初中学业水平考试的压轴题，试题的3道小题之间有联系，但不是递进关系，因而学生能否正确解答前面的问题对后面的影响不是致命性的，某一个结果的偶然失误或错误，对后面的解答影响较小.这样的设计，在一定程度上确保了试题有较高的信度.

影响信度的原因很多，以下几种情况的试题，信度存在一定的问题.

（1）题型设计不尽合理，难以准确测量学生的真实水平.

例10分式方程的解是（）.

（A）x＝1 （B）x＝-1

（C）x＝2 （D）x＝-2

【评析】如果此题是从解分式方程的角度对学生进行考查，因为学生在解答此题时，可以直接将四个选择支逐一代入验证得到正确答案，不需要掌握方程的解法，所以并没有有效地考查分式方程的解法，所以信度低.

例11定义1：与四边形四边都相切的圆叫做四边形的内切圆.

定义2：一组邻边相等，其他两边也相等的凸四边形叫做筝形.

探究：任意筝形是否一定存在内切圆？

答案：_________.（填“是”或“否”.）

【评析】此题立意较好，重在考查学生的基本活动经验，即学生在研究很多平面图形的基础上，用获得的经验来研究新的图形.但此题有两个新知识需要学生阅读并理解，使用填“是”或“否”这样的填空题题型，会使一部分学生无需思考直接猜测而获得正确答案，这对认真研究这个问题的学生来说是非常不公平的，也无法体现学生能力的差异性.因此，此题运用填空题题型不够合理、科学，信度不高.

（2）难度过大，绝大多数学生都不会.

例12已知抛物线，顶点C(1，-3)，与x轴交于A，B两点，A(-1，0).

（1）求这条抛物线的解析式.

（2）如图5，以AB为直径作圆，与抛物线交于点D，与抛物线的对称轴交于点E，依次连接A，D，B，E，点P为线段AB上一个动点（点P与点A，B不重合），过点P作PM⊥AE于点M，PN⊥DB于点N，试判断是否为定值.若是，求出此定值；若不是，说明理由.

（3）在（2）的条件下，若点S是线段EP上一点，过点S作FG⊥EP，FG分别与边AE，BE相交于点F，G（点F与点A，E不重合，点G与点E，B不重合），判断是否成立.若成立，给出证明；若不成立，说明理由.

图5

【评析】这是一道初中学业水平考试压轴题，作为综合题，考查的知识点都是重要的.但是因图形过于复杂，解答过于烦琐，加上解题时间有限，在某种程度上会引起学生不必要的心理紧张，从而干扰学生客观反映自己的实际水平.在实际考试中，就连优等生也会放弃解答，所以信度低，区分度也不高.

（3）题意晦涩难理解，或文字表述过长、字母过多，让有能力解答的学生也望而生畏.

例13正方形ABCD的对角线交点为O，两条对角线把它分成了四个面积相等的三角形.

（2）四边形ABCD的两条对角线互相垂直，交点为O，若△AOB，△BOC，△COD，△DOA面积分别为S1，S2，S3，S4，试判断S1，S2，S3，S4的关系，并加以证明；

（3）四边形ABCD的两条对角线交点为O，若△AOB，△BOC，△COD，△DOA面积分别为S1，S2，S3，S4，试判断S1，S2，S3，S4的关系，并加以证明；

（4）四边形ABCD的两条对角线相等，交点为O，∠BAC=∠BDC，若△AOB，△BOC，△COD，△DOA面积分别为S1，S2，S3，S4，试只用S1，S3或只用S2，S4表示四边形ABCD的面积S.

【评析】这是一道初中学业水平考试压轴题，渗透了对从特殊到一般的数学思想的考查，立意较好，难度也呈梯度分布，入口较易.但此题没有一个图形，这样长篇的文字、符号语言的叙述，而且各小题的表述形式又大致一样，会给学生造成较大的视角压力，让已经做到最后一题且有能力解答此题的学生也因畏惧而放弃，所以信度不高，区分度也不高.

3.区分度

区分度是指考试结果能否区分不同层次学生的指标.区分度与效果、信度、难度密切相关.

在常模测量的高考中，区分度是通过计算试题的标准差来分析的.初中学业水平考试是标准测量，主要通过经验把控和成绩分析来评价区分度.

提高区分度的方法有：降低试题入口的难度，通过问题串（或改变题型）逐步提高问题深入的难度；通过增加或删除符号语言、图表语言，增加或降低题目阅读理解的难度；设置开放性问题；增加试题的选择性（两道试题中选做一题）；同一试题，因解法不同，设置不同的评分标准；等等.

例14 在平面直角坐标系中，有A(2，3)，B(3，2)两点.

（1）再添加一点C，求出图象经过A，B，C三点的函数关系式.

（2）反思第（1）小题，考虑有没有更简捷的解题策略？说出你的理由.

此题给出的评分标准如下.

（1）①如果先设一点C，并按二次函数模式求出解析式的给5分；

②如果将A，B两点，按一次函数直线模式求解析式的，再在此直线上找到一点C的给7分；

③如果直接看出A，B两点均在双曲线上，由此找出点C的坐标的也给7分；

（2）反思第（1）小题，若按上述①做，再按②和③找到有简捷者，又给4分，此题得全分9分.

若按上述②做，又通过①说明此为较简捷者再给1分，若还找到③种方法，再给1分.

若按上述③做，又通过①或②说明③最简捷，再给2分.

另：学生只要有此①②③种思路解题.若计算错误，可酌情给分，重点考查学生的发散思维，所以只要思路正确即可得分.

【评析】此题是条件、结论和解题策略均开放的问题.因解答结果不同，考查的效度、难易度不同，所以设置了不同的评分标准.

从给出的评分标准不难看出，此题重在对学生数学思维的复杂、深刻程度进行区分.第（1）小题中添加的点C的不同，得到不同的函数图象，如直线、双曲线与抛物线都可以得到，但解题的繁易和思维的深刻性却不一样，评分标准分别给了5分和7分，以区分不同层次的学生.

4.难度

难度是指试题的难易程度，是评价考试的一个非常重要的指标.一道题目，如果大部分学生都能答对，那么这道题目的难度就小；如果大部分学生都不能答对，那么这道题目的难度就大.

合适的难度，才能有效地测量学生的真实水平，才能有效地区分不同层次的学生.因此，把握好试题的难度是贯穿具体命题工作全程的问题.

控制试题的难度有很多方法，简单举例如下.

（1）改变题型.

选择题、填空题、解答题因呈现的形式不同，所考查的知识与能力的侧重也就不同，难度自然就不同.

例15等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（）.

（A）60° （B）120°

（C）60°或150° （D）60°或120°

【评析】等腰三角形是初中几何学习最重要的基础图形之一，所涉及的知识和技能都是初中数学的核心内容.由于此题涉及两类图形的计算（高在三角形内部或高在三角形外部），如果以解答题或填空题的形式出现，学生容易忽略高在三角形外部这种情况，而以选择题的形式出现，由于有选择支的提示作用，学生自然会联想到分类研究，因此难度有所降低.

（2）具体化与形式化.

具体化与形式化是认识问题的两种手段.当我们对问题不熟悉时，往往需要从具体、特殊的情形入手，发现问题的立足点以及不同信息之间可能有的联结关系；而当我们对问题的研究到达一定的深度时，则需要揭示出一类问题的一般规律，并用形式化的数学语言加以表述.在调整试题难度时，我们也常常采用把问题具体化后呈现以降低难度，或把具体问题形式化后呈现以增加难度.

例16若y关于x的函数y=(a-2)x2-(2a-1)x+a的图象与坐标轴有两个交点，则a可取的值为____.

【评析】此题将常见的数字系数改为字母系数，同时给出图象的大致位置，要求学生写出与这种大致位置相关的一种特殊的二次函数，答案转变成了开放的形式，显然难度加大了.

（3）增加或减少铺垫.

在解答题的求解过程中，解决问题步骤的多少在很大程度上影响着试题的难度.如果一道解答题的求解步骤较多，那么增加或减少铺垫就能有效地改变其难度.

例如，在没有图表语言表述的试题中，增加图表可以降低难度；在需要添加辅助线的几何证明题中，给出辅助线提示可以降低难度；在难题中，增加选择题或填空题可以降低难度，等等.相反，改编可以增加难度.

（4）增加或减少限制条件.

通过改变常见题目的条件，可使原题目的难度发生变化.有时，增加限制条件能降低难度，有时则可能导致题目难度上升.

例17如图6，王虎使一长为4cm，宽为3cm的长方形木板，在桌面上做无滑动的（顺时针方向）翻滚，木板上点A位置变化为A→A1→A2，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A2位置时共走过的路径长为（）.

图6

【评析】如果只有一次翻滚，则题目就比较常规，适合考查技能层次的数学学习水平.此题让木板翻滚了两次，第二次翻滚还加上了“小木块挡住”的条件，使此题的解答难度得到了提升，因此在一定程度上可以考查不同层次学生的数学学习水平.

5.教育性

以下的例题，只分析其在数学文化价值、课程改革理念，以及教法、学法导向等方面的教育价值.

例18如图7（1）所示的是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的.若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图7（2）所示的“数学风车”，则这个风车的外围周长是_______.

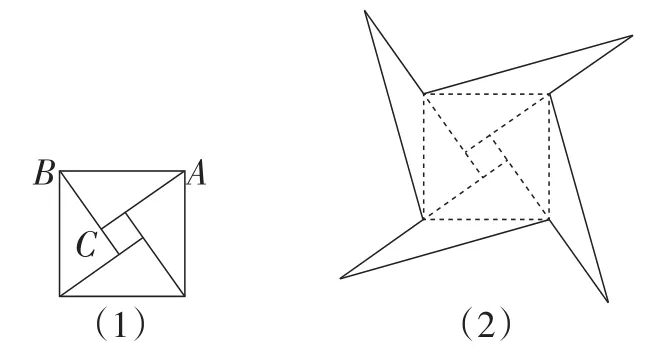
图7

【评析】“数学风车”本身就是一种文化现象，蕴含丰富的数学内容，使得此题在考查勾股定理的同时，还能对学生进行古代数学文化的熏陶，较好地体现了数学的文化价值.

例19文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出了“已知”和“求证”.已知：如图8，在△ABC中，∠B=∠C，求证：AB=AC.她们对各自所作的辅助线描述如下.

图8

文文：过点A作BC的中垂线AD，垂足为点D；

彬彬：作△ABC的角平分线AD.

老师看了两位学生的辅助线作法后说彬彬的作法是正确的，而文文的作法需要订正.

（1）简要说明文文的辅助线作法错在哪里.

（2）根据彬彬的辅助线作法，完成证明过程.

【评析】将课堂教学过程中经常发生的作辅助线的错误置于中考情境中进行考查，不仅有利于教师日常教学中更加细致严密地关注教的过程，而且有利于学生平时形成良好的学习反思习惯.这种对教与学的良好导向，值得在命题中加以提倡.

例20下边是一元二次方程求根公式的两种推导方法.

阅读并回答下列问题.

（1）两种方法有什么不同？

（2）你认为哪个方法好？说明你的理由.

【评析】此题是由教材中的正文内容改编的，方法2是对教材方法的再创新.它说明教材不只是教师的教学之本，更是教师的学习之本、研究之本.对学生而言，教材也不是绝对神圣的，要鼓励学生善于从教材中发现问题、提出问题、解决问题，让教材成为学生知识再创造的重要源泉.这就是此题体现的难得的教育价值.

此题参考答案如下.

方法1出现分式配方比较繁；两边开方时分子、分母都出现“±”，相除后为何只有分子上有“±”，不好理解.更重要的是容易误认为方法2就无上述问题.

三、试题编制技术

通过前两部分的分析，我们已经清楚题型及效度、信度、区分度、难度和教育性调控技术是编制试题的基础，以上的例题对题型及调控技术在编制试题中的应用已经进行了很多说明和分析.例如，改变题型、将题目的条件与结论互换、运用不同语言呈现题目、增加或删减题目的条件、不同学科的融合、由教材题目改编、由实际生活创编、由现实世界提炼.

关于试题编制技术，这里只从命题途径的视角，对上边提到的最后三个途径加以分析.

1.由教材中题目改编

例21先化简，再求值：，其中.

【评析】此题是将教材中的习题赋予了一个实际情境.这说明计算题的原型问题有时也与人们的日常生活紧密联系，如果能将这些单纯的计算题进行类似的改编，既能保证题目的效度，也能使试题显现出一些“人情味”，使冰冷的中考泛出些温情.

不过，利用纯计算题编制具有生活情境的计算题，必须保证改编的计算题符合实际问题情境，所选取的生活情境越贴近生活越好.

例22陈师傅带着7岁的儿子去参加朋友的一个聚会，儿子发现，每两人见面后都要握手，他好奇地数握手次数，一共握了28次，你知道到会的人有多少吗？

例22的改编题：陈师傅带着7岁的儿子去参加朋友的一个聚会，儿子发现，每两人见面后都要握手，他好奇地数握手次数，一共握了28次，你知道到会的人有多少吗？请你联系生活实际或所学知识，编写其他的问题，使所列的方程与这个问题的方程相同，或列方程的思想是相同的.

和这个问题所列方程相同的实际问题很多，简单举例如下.

（1）多个村庄，每两个之间都有一条公路，若有人统计共有28条公路，问共有多少个村庄？

（2）在某两地的铁路线上，共有28个不同的火车站，问这条铁路最多共有多少个不同的票价？

（3）某乒乓球循环赛，每个队都要见面，共举行了28场比赛，问共有多少个代表队参加？

（4）平面上有28条直线，若任意两条不平行，任意三条不共点，则有多少个交点？

（5）空间n个点，任意三点不共线，可以连28条不同的直线，求n的值.

和这个问题列方程思想一样的实际问题也很多，简单举例如下.

（6）春节前，几个人互打电话问候，若共打了28次电话，问共有几人？

（7）元旦前，几个同学互相赠送贺年卡，若共赠送了28张贺年卡，问共有几人？

（8）在某两地的铁路线上，共有28个不同的火车站，问这条铁路共需设计多少个不同的火车票？

【评析】改编后的试题具有很强的开放性，不仅很好地展示了数学的一题多变、一题多解、多题一解功能，而且很好地考查了学生提出问题、分析问题和解决问题的能力，以及创新意识和应用意识.

2.由实际生活创编

例23鞋子的“鞋码”和鞋长（cm）存在一种换算关系，表2是几组“鞋码”与鞋长换算的对应数值（“鞋码”是表示鞋子大小的一种号码）.

表2

（1）设鞋长为x，“鞋码”为y，试判断点(x，y)在你学过的哪种函数的图象上；

（2）求x，y之间的函数关系式；

（3）如果某人穿的鞋“鞋码”为44号，那么他的鞋长是多少？

【评析】此题主要考查一次函数的概念和图象性质，但赋予了它切合学生实际生活的情境，在保证效度的基础上，很好地体现了数学的应用价值.

3.由现实世界提炼

例24“中山桥”是位于甘肃省兰州市中心、横跨黄河的一座百年老桥.如图9（1）所示，桥上有5个拱形桥架紧密相联，每个桥架的内部都有一个水平横梁和8个垂直于横梁的立柱，气势雄伟，素有“天下黄河第一桥”之称.如图9（2），一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图9（2）所示的平面直角坐标系，跨度AB=44米，∠A=45°，AC1=4 米，点D2的坐标为(-13，-1.69)，则桥架的拱高OH的值为_______.