借平移旋转之变 筑推理论证之路——以平移旋转的解题教学指导为例

向 隽

（湖北省秭归县实验中学）

在各版本初中数学教材中，都编入了平移、旋转这一内容.对于这部分内容，教学时从哪里着力，才能引领学生更好地、整体地洞察图形结构并推理图形中相关的位置与数量关系？

笔者认为，针对平移、旋转内容的教学，一是从数学教学内容的角度用力，欣赏平移和旋转带给世界的美的同时，落实平移和旋转这一核心知识点；二是从解题策略的角度用力，渗透把平移、旋转作为推理论证的依据，提升学生的思维能力.

本文仅从数学解题的角度，以例题呈现的形式，探讨在解题教学中，如何指导学生用平移、旋转的知识和思路，优化解答策略.

一、借用平移旋转求坐标，落实核心知识点

例1如图1，将△ABC绕点C(2，-3) 旋转180°得△DCE，设点A的坐标为A(m，n)，求点D的坐标.

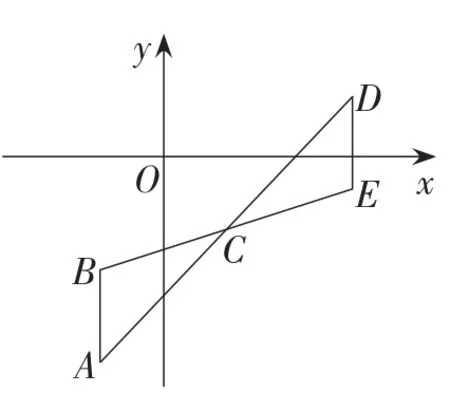
图1

图2

解析：如图2，将线段A D向上平移，使点C经过点O，根据点C与点O的坐标，发现平移规律，从而得到点A平移后的坐标为M(m-2，n+3).点D平移后到达点N的位置，M与N关于原点中心对称，从而得点N的坐标为N(2 -m，-n-3).再将点N向下平移3个单位，向右平移2个单位即可得到点D的坐标为D(4 -m，-n-6).

图2的解法为将点A向左上平移，根据点C的平移规律，求出点M的坐标，再将点N向右下平移，退回到原来的位置，从而求出点D的坐标.

此题也可以按图3所示的方法进行解答，即过相关的点作x轴或者y轴的平行线，构造直角三角形，利用全等及相关知识解决问题.

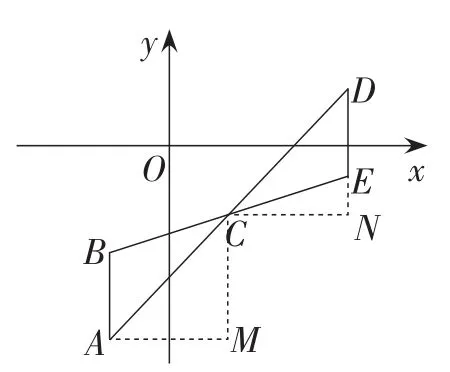
图3

对比两种解法，图2是依据题目条件，直接借助点的坐标平移规律，一移一退，直取目标；图3是回溯三角形全等及坐标的几何意义这一知识元.显然图2中着眼于点的平移特征及点的坐标平移的数量关系，平移线段AD，巧用原点的坐标特点找规律，图形简洁明了，计算过程简单，结果一目了然.

例2如图4，点A的坐标为A(-2，-3)，点C的坐标为C(m，n)，将AC绕点A逆时针旋转90°得AB，求点B的坐标.

图4

图5

解析：如图5，将线段AC向右平移2个单位，向上平移3个单位，使平移后的点A刚好经过点O，此时点C平移到点E的位置，得到点E的坐标为E(m+2，n+3).根据△OEF≌△DOG可得点D的坐标为D(-n-3，m+2).再将线段OD退回到线段AB的位置，从而得到点B的坐标为(-n-3-2，m+2-3)，整理得B(-n-5，m-1).

此题可以用两种方法求解，一是如图5，通过平移线段的方法，将点A平移到原点的位置，找出平移的规律，求出线段上另一个端点的坐标，利用全等相关知识，求出平移后旋转点的坐标，再将点D退回到原来的位置，得到要求的点B的坐标.二是如图6，过点A作x轴的平行线，分别与过点B，C作y轴的平行线相交于点D，点E，则有△ADB≌△CEA，根据线段AE=m+2，CE=n+3，得到线段AD=n+3，BD=m+2，从而求得点B的坐标为B(-n-5，m-1).

图6

两种方法都是立足于点的坐标和三角形全等这一知识元而进行图形构建，所不同的是，图5是构建全等后转化为方程，而图6中是回到图形平移的性质，紧扣平移规律，先进再退，直观可得.

二、活用平移旋转求线段，明晰推理依据

例3如图7，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，若四边形ABCD的面积是24 cm2.求AC的长.

图7

图8

解析：如图8，将△ADC以点A为中心按顺时针方向旋转90°至△ABE处，则边AD与边AB刚好完全重合，∠EAB=∠CAD，∠EBA=∠CDA，AE=AC，所以∠EAC=∠EAB+∠BAC=∠CAD+∠BAC=∠BAD=90°.因为∠BAD+∠BCD=2×90°=180°，所以∠ABC+∠ADC=360°-180°=180°.于是∠ABC+∠ABE=180°.故E，B，C三点共线，可知△AEC为等腰直角三角形.过点A作边EC上的高AF，则，所以. 于是，则.

此题主要考查四边形中有关线段的计算.利用旋转的知识将△ADC绕点A顺时针方向旋转到△ABE的位置，从而得到△AEC是等腰直角三角形.利用等腰直角三角形的特殊性质求出高AF和底边EC之间的关系，再根据△AEC的面积求得AC的长.通过旋转将任意四边形转化成学生熟悉的等腰直角三角形来解决问题，化难为易，这也正是解决四边形有关问题的常用方法.

当然，也可以在如图9所示的图形中，过点A作AE⊥BC于点E，AF⊥CD交CD的延长线于点F，然后证明Rt△ABE≌Rt△ADF，得四边形AECF为正方形，通过面积割补得，从而求出.这种方法本质上可以从图形旋转的性质中找到计算推理的依据.

图9

三、灵动平移旋转求角度，优化推理思路

例4如图10，正方形ABCD内有一点P，∠PAD=∠PDA=15°，连接PB，PC，试问△PBC是等边三角形吗？为什么？

图10

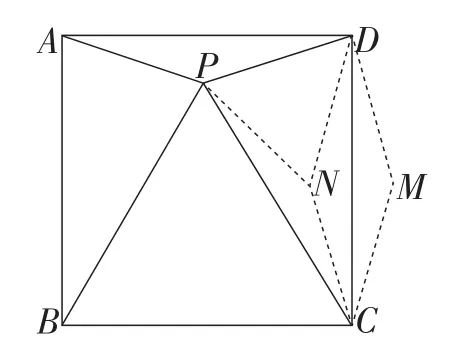
图11

解析：如图11，将△APD绕点D逆时针方向旋转90°，得到△DMC，再作△DMC关于DC对称得△DNC，则△DNC≌△DMC≌△APD.因为PD=ND，∠PDN=90°-15°-15°=60°，所以△PDN是等边三角形.所以∠PND=60°.则∠PNC=150°.根据PN=DN=CN，可得∠PCD=30°.则∠PCB=60°.所以PC=BC=PB.则△PBC是等边三角形.

此题关键是说明∠PCD=∠PBA=30°，利用已知条件可以设想将△APD绕点D逆时针方向旋转90°，而使点A与点C重合，此时问题得到解决.解法中通过旋转有机地将看上去不相关的线段和角联系在一起，再根据旋转的性质得到一系列的等腰三角形和等边三角形，为后续部分解决问题带来方便.这一解答思路，实质上是对图形旋转的性质这一知识点有深层的理解，并把图形旋转的性质作为推理论证的依据，从而优化了推理论证思路.

例5如图12，点E，F分别是正方形ABCD的边BC，CD上一点，且BE+DF=EF，求∠EAF的度数.

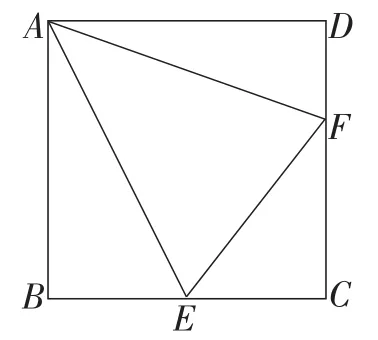
图12

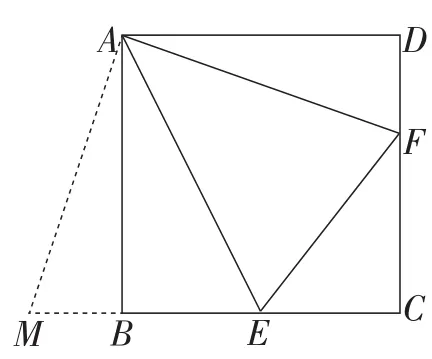
图13

解析：如图13，将△ADF绕点A顺时针方向旋转90°到△ABM的位置，则AD与AB重合.因为△ADF≌△ABM，∠ABM=∠ADF=90°=∠ABE，所以∠ABM+∠ABE=180°，则M，B，E三点共线.则有△AME≌△AFE，所以∠MAE=∠FAE=45°.

用旋转的方法将△ADF和△ABE整合在一起，凑成一个新的三角形，将不相关的线段、角集中到一起，构成△AME，再寻找与其全等的三角形，使问题迎刃而解.此题除了上述旋转方法外，也可以如图14所示，将△ABE绕点A逆时针旋转90°到Rt△ADG的位置，也可以叙述为延长CD至点G，使DG=BE，连接AG，同样可以求解.无论哪种方法，其本质都是利用旋转三角形的性质作为推理的依据来解决问题.

图14

四、妙用平移旋转求面积，彰显转化策略

例6如图15，将一块含30°角的直角三角板ABC绕点B顺时针旋转45°至△EBD的位置，其中∠BAC=30°，BC=6，则边AC扫过的阴影面积为多少？

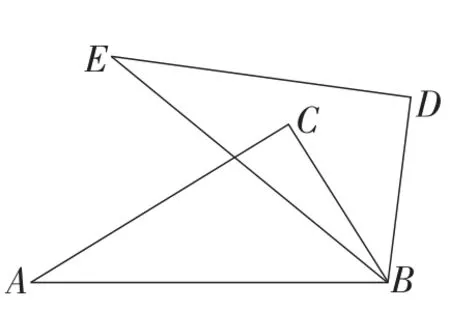
图15

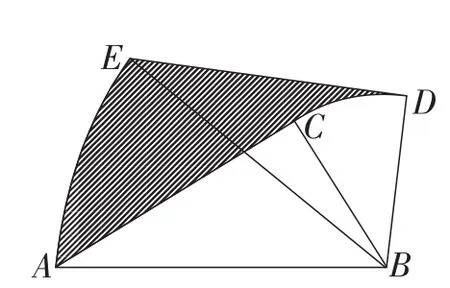
图16

解析：如图16，旋转过程中，点A到点E的路径是以点B为圆心，AB为半径的一段弧，点C到点D的路径是以点B为圆心，BC为半径的一段弧，所以. 从而得.

仔细分析这道题，从旋转角度入手，继续将△ABC绕点B按同样的方式旋转，7次后，可以得到8个面积相等的扫过的图形面积，最后的图形正好回到学

生熟悉的圆环面积，所以AC扫过的面积为.这样利用图形旋转性质，并把图形旋转有意识地作为解答思路中的一种转化策略，尝试连续旋转，就把不规则的几何图形转化成了学生常见的而且非常熟悉的图形，问题解决就变得简单直观.

五、尝试圆与平移旋转，发挥其工具性效用

例7如图17，在平面直角坐标系中，⊙P的圆心坐标是P(3，a)(a＞3)，半径为3，函数y=x的图象被⊙P截得的弦长AB为，求a的值.FD=OD=PE.在Rt△FOD中，·(a-3)，在Rt△PEB中，，则有

图17

图18

解析：如图18，将直线AB向上平移使其经过点P，交y轴于点F，设直线PF的解析式为y=x+b，因为直线经过点P，所以有a=3+b.变形得b=a-3.过点F，P分别作直线AB的垂线，垂足分别为点D，E，则有.解得.

上述解法利用平移的性质，立足于平移知识，并将平移作为沟通图形的工具，把与圆不相关的直线与圆进行关联，自然构建垂径定理得解.在解答中，将直线y=x向上平移，使其经过圆心P，利用函数思想来解决问题.将平移后的直线与y轴交点的纵坐标用a表示出来，进而得到线段FD的长.再利用勾股定理、垂径定理等知识求出线段PE的长，利用线段相等构造方程，求出a的值.

此题也可过点P作x轴的垂线，利用求线段的长度来转化进而求点的坐标.比较两种思维方式，平移直线AB，构造关于a的方程，利用函数思想、数学建模的思想，求出a的值，解决问题简洁明了.

六、写在最后

以平移和旋转立意为背景的中考题常见而又有创意，这类题在考查学生基础知识和基本方法的同时，注重学生的基本数学活动经验和动手操作能力.借助试题讲评与指导构思解题教学时，我们应当从哪里用力？怎样有意地向学生渗透平移旋转的知识性、依据性和工具性？

伟大的数学家华罗庚先生告诫我们：复杂的问题要善于退，足够地退，退到最原始而不失去重要性的地方，是学好数学的一个诀窃.例1和例2回到平移和旋转知识去求点的坐标，正是基于教材习题的再生长，复习平移和旋转知识点的同时，自觉将其内化成方法.用平移退回到原点求解，不失为一种适合学生的解题方法，比用“一线、三直角”构造全等转化的方法要清楚、快捷.

运用旋转性质，并把图形旋转性质作为推理的依据，正是基于平移和旋转不改变图形的形状和大小等基本几何变换性质，进行自觉分析与挖掘，在割补法经验基础上，自然联想，顺利求出例3中的线段AC的长；例4和例5是很典型的利用图形旋转法解题的例子，由于每名学生处理问题的视角和习惯不同，选择的旋转中心和旋转方向不同，可以得到不同的解题思路，但是都能顺利求出角的度数，在此题基础上，可以借助旋转，进行一系列生长和变化.

一只站在树上的鸟儿，从来不会害怕树枝断裂，因为它相信的不是树枝，而是自己的翅膀.正是因为对图形平移和旋转性质理解比较透彻，把图形旋转提升到推理及转化的工具性位置，并将其作为一种解题策略的转化手段，才会在整体思想的理念下对例6依次旋转8次，回归到圆环面积，以较高的思维代价，取代繁杂的图形分割和计算，深层次揭示出题目的内在结构，借助圆的旋转不变性，以及图形完美性可以解决很多几何问题.解题时，如果将其与平移和旋转相融合，可以像例7和例8那样，快速、完美地获得解题思路.

《义务教育数学课程标准（2011年版）》（以下简称《标准》）对图形变换教学作出了统一规定和要求，明确图形变换具有知识性、依据性和工具性的特征，让学生养成用变换的观点思考图形和图形之间的关系，拓宽解决图形问题的思路.章建跃博士指出，数学教学应该前后一致，逻辑连贯，一以贯之，对一些基本的、可迁移的、可生长的元知识、元方法狠下功夫.想要从日常教学资源中发现数学知识生长的“种子”，关键是要对数学有深刻的理解.鉴于此，笔者认为，平移与旋转既是《标准》要求学生掌握的核心知识点，更重要的也是核心方法.

教学平移和旋转内容时，要教会学生理解教材、思前想后、关联整合、串点成线，把平移和旋转从知识点上升到一种解决问题的方法，能够将其作为处理图形性质与位置常用的自觉思考意识，就会巧妙解答几何计算题和证明题.基于从学生熟悉的知识点和图形性质出发，为学生解题思路的生长，种下有生命力的“种子”.