形如a+λb型结构最小值问题的解法及溯源
——基于HPM的数学拓展性课程教学资源研究
2018-12-04陆祥雪
陆祥雪
(江苏省泰州中学附属初级中学)
几何最值问题作为几何计算的一种题型,在中考试题中屡见不鲜.其主要解题方法有两种,一种是选用适当的变量,写出几何量的表达式,然后对表达式进行讨论(代数方法);另一种是利用图形的几何特性,找到取得最值的位置,然后再求最值(几何方法).对于一些问题,我们常常需要进行转化,然后再用上述方法进行解决.a+λb型结构作为a+b型最小值问题的变式,其解答的方法也不例外.
一、问题与解析
问题1:如图1,在△ABC中,BA=BC=4,∠A=30°,D是AC上一动点,求的最小值.

图1
方法1:如图2,将点B沿AC翻折得点B′,此时B′D=BD. 当B′,D,F三点共线时(如图3),的值最小,最小值为B′F的长,B′F=B′Csin60°=.

图2
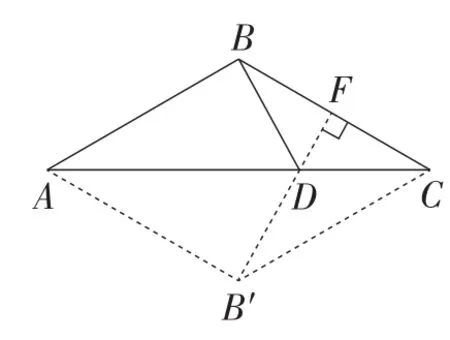
图3
方法2:如图4,将BC沿直线AC翻折,得直线CE.这样∠BCA=∠ACE,过点D作DE⊥CE于点E,则当B,D,E三点共线时,BD+的值最小,最小值为BE的长,即BE=BCsin 60°=.

图4
问题2:如图5,在△AOB中,∠AOB=90°,OA=4,OB=3,E是OA上一点,且OE=2,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0 °<α<90°),连接E′A,E′B,求的最小值.
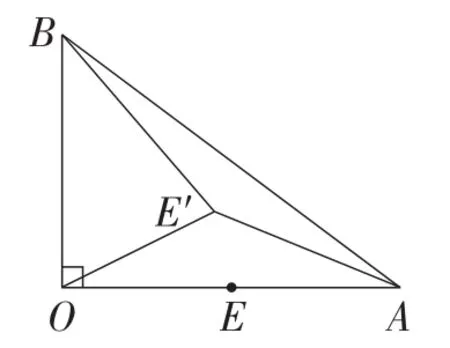
图5
如图6,在OB上取点F,连接E′F,由“两边对应成比例且夹角相等的两个三角形相似”可知,当时,△OE′F∽ △OBE′,所以所以,这样,问题转化为求AE′+E′F的最小值,所以当A,E′,F三点共线时,E′A+E′B的值最小,即为线段AF的长,AF的长为.

图6
以上两个问题均是通过几何方法求解的,关键是将a+λb中的λb转化为一条线段,其作法可以认为是通过构造相似三角形,利用相似的性质实现转化.解题的依据一种是应用“垂线段最短”;另一种是应用“两点间线段最短”.
二、问题与溯源
上述两个问题均涉及两个定点及一个动点,但问题1的动点是在一条过定点的直线上运动,问题2的动点实际上是在一个圆上运动.追溯这两个问题的背景,涉及到两个有趣的问题.
1.“胡不归”问题
从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路回家.由于思父心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径,而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭.邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?”这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归”问题.
小伙子设想了一条回家路线,如图7,A是出发点,B是目的地,直线l是一条驿道,而驿道靠目的地一侧全是砂土地带,为了尽快回家,小伙子选择了直线路程AB.但是,他忽略了在驿道上行走要比在砂土地带行走快这一因素.如果他能选择一条合适的路线,是可以提前抵达家门的.那么,这合适的路线应该是哪条路线呢?
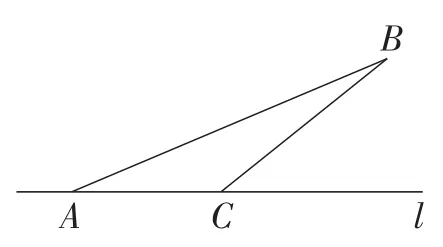
图7
显然,根据两种路面的状况和在其上行走的速度,可以在直线l上选定一点C,小伙子先从点A走到点C,然后从点C折往点B,可以最早到达点B.假设小伙子在驿道上行走的速度为m米/时,在砂土上行走的速度为n米/时(n 图8中,过点C作CD⊥AM,则,所以.由“垂线段最短”可知,当B,C,D三点共线时,t的值最小,最小值为. 这就是问题1的背景,也给出了这个问题的一般解法.射线AM为什么作在点B关于直线l的异侧?其实,作在同侧也可以,不过此时就要作点B关于直线l的对称点,就是将△ABC沿直线l翻折下来,相比较多了一些解题的步骤.我们可把问题1归纳为下列模型:“两定点+一动点”求a+λb最小值,动点在过一定点的定直线上运动,我们不妨称之为“胡不归”模型.在模型识别时需要注意在a+λb中,0<λ<1. 变式:如图9,在△ABC中,,AD⊥BC于点D,且AD=4,P是AD上的动点,求的最小值. 图10 在平面上给定相异两点A,B,设点P在同一平面上且满足,当k>0,且k≠1时,点P的轨迹是个圆,这个圆我们称之为阿波罗尼斯圆.这个结论称之为阿波罗尼斯轨迹定理.设M,N分别为线段AB按定比k分割的内分点和外分点,则MN为阿波罗尼斯圆的直径,且这个定理的证明在高中阶段是用建立坐标系的方法解决的,这里用平面几何的方法来解决. 完备性,即满足条件的点P均在同一个圆上. 图11 如图11,过点A作AC∥PM,交BP的延长线于点C,过点B作BD∥PA,交PN于点D. 由角平分线逆定理,可得PM平分∠APB,PN平分∠QPB. 所以∠MPN=90°. 所以点P在以MN为直径的圆上. 设AB=a, 纯粹性,即以MN为直径的圆上的点均满足以上条件. 图12 如图12,过点P作PH⊥MN于点H,设BH=b, 我们还可以推得阿波罗尼斯圆的半径与圆心到线段两端的距离之间的关系. 如图13,设直径为MN的圆的圆心为点O,连接PO, 图13 所以OP2=OB·OA. 所以这个关系可概括为,阿波罗尼斯圆的半径是圆心到线段两端的距离的比例中项. 由此可知,当点P在⊙O上运动时,已知直径MN,即已知线段AB的内、外分点,利用OP2=OB·OA,在A,B两点中,如果已知一个点,那么就可以确定另一个点及的比值,因为此时. 在问题2中,动点E′在以点O为圆心,半径为2的圆上运动,⊙O为阿波罗尼斯圆,B是已知线段的一个端点,根据阿波罗尼斯圆的性质,我们可以在OB上找到线段的另一个端点(设为点F),所以有,这样,从而将问题转化. 我们可以把问题2归纳为下列模型:已知两个定点求a+λb最小值,动点在一个圆上运动,根据以上讨论,实际上是,已知阿波罗尼斯圆及线段的一个端点,确定另一个端点的问题,也就是阿波罗尼斯圆问题的一个变式,λ的值即为半径与圆心到线段已知端点距离的比或倒数.利用此模型通过更换问题背景可以编拟出如下新问题. 题目如图14,四边形ABCD是边长为4的正方形,AM=1,N是BC边上一个动点,将△BMN沿MN折叠,使点B的对应点P落在正方形ABCD所在平面内,Q是BC的中点,求PQ+3PA的最小值. 图14 数学是人类文化的重要组成部分,数学素养是现代社会每个公民应该具备的基本素养.以数学史料为命题素材的问题,在历年中考中也时有出现,通过对这些问题的研究,感受数学历史及相关内容的有趣故事,对提升教师自身的数学素养,以及对提高数学教学研究的兴趣大有益处.教材及学生平时遇到的数学问题,限于篇幅,没有提供数学知识产生的历史背景、发现者的原始思考及来龙去脉,这使得火热的发现变成冰冷的美丽.教师及学生了解数学史对全面而准确地理解数学、培养数学素养、提高教学质量,都是十分有益的,让学生学习有文化的数学,在学习数学的同时,获得文化的熏陶. 教师在平时的教学工作中,会接触到大量的数学问题,对这些问题的态度也影响到教师的成长.有些教师能以问题为素材,不断探寻问题的内涵与外延,力求理顺问题的来龙去脉,并对问题的解答进行整理、归纳,努力找到问题的模型,得到普适的方法,追溯问题产生的背景,了解命题者的考查意图.如果在教学中,教师都努力这样做,对培养学生的抽象概括的数学核心素养,以及提出问题和解决问题的能力大有裨益,使学生能解一题、会一类,这样才能使更多的充满数学味道的问题为提升学生的数学素养服务.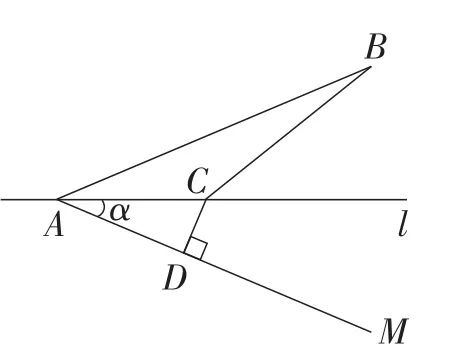


2.阿波罗尼斯圆
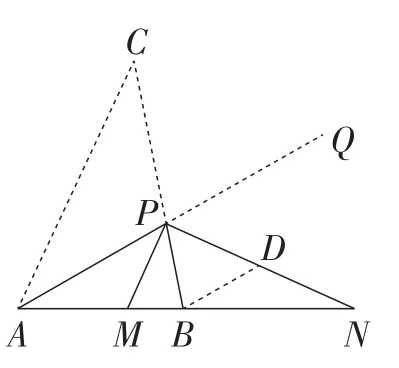




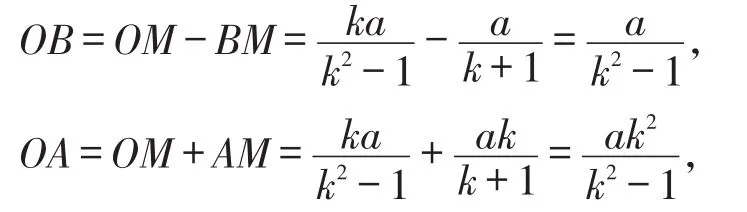

三、问题与思考
