只用刻度尺画图问题的设计与思考

朱建明

（江苏省南京市教学研究室）

刻度尺是最常见的画图和度量工具，它可以画直线、射线和线段，也可以度量线段的长度.只用刻度尺画图就是画图时使用的工具仅限于刻度尺，不能运用圆规等其他工具，它与尺规作图有着本质的区别.只用刻度尺画图的问题虽然看似只是在画图，但其蕴含了丰富的图形与几何知识和方法，思维价值高，能激发学生的探究兴趣，培养学生的几何直观和逻辑推理能力.在数学教学中，设计系列化的只用刻度尺画图问题，既能创设新颖别致的问题情境，也能为高效课堂建设提供丰富的资源素材.下面谈谈笔者在设计课题学习“只用刻度尺画图”中的问题串时的思考.

一、构造等腰三角形

用刻度尺可以画出一定长度的线段，因此可以画等腰三角形.根据这一特性，可以设计一些只用刻度尺画图的问题，而构造等腰三角形是解决问题的主要途径.

例1如图1，只用刻度尺，画出∠BAC的角平分线.

图1

设计初思考：用单一工具画图，见到比较多的是只用圆规画图和只用无刻度直尺画图，鲜见只用刻度尺画图.而只用刻度尺画图，首先要考虑它能画哪些基本图形，能画等腰三角形吗？答案是肯定的.只用刻度尺，不仅能画等腰三角形，还能画等腰三角形底边上的中线.由于等腰三角形底边上的中线与顶角的角平分线重合，因此，将图形分拆，隐去等腰三角形的底边后，便是一个角和它的平分线，于是有了例1.

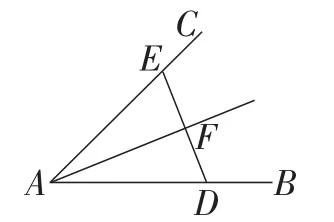
图2

画图方法：如图2，用刻度尺在∠BAC的边AB，AC上分别取点D，E使AD=AE，连接DE，量出DE的长，取DE的中点F，再画射线AF，则射线AF即为∠BAC的角平分线.

此例实际上是用刻度尺构造等腰三角形，利用等腰三角形“三线合一”性质画出角平分线.此例可以在等腰三角形的性质的相关教学中使用，也可以在三角形全等的判定的相关教学中使用.

二、构造直角三角形

只用刻度尺可以画直角三角形，根据这一特性，可以设计一些问题，解决这些问题的方法之一就是构造直角三角形.

例2只用刻度尺，画出一个直角∠BAC.

设计初思考：只用刻度尺，能画直角三角形吗？答案也是肯定的.只不过相对于画等腰三角形，画直角三角形要复杂一些，需要画腰长相等、一腰重合的两个等腰三角形.直角三角形最典型的特征是有一个直角，于是提出例2这个问题.

画图方法：如图3，用刻度尺画出一定长的线段BC，取BC的中点D，画线段AD，使AD＝BD，连接AB，AC.则∠BAC即为直角.

图3

此例就是构造直角三角形，继而画出一个直角.当然这个问题还可以利用刻度尺画两条互相平分且相等的线段，那么线段的四个端点构成一个矩形，也可以画出直角或直角三角形，而这相当于画出两个斜边重合的直角三角形.

此外，根据此题用刻度尺画直角的方法，还可以判定直线与圆是否相切.如图4，点A是⊙O上的点，点P在⊙O外，用刻度尺取OP的中点B，连接AB.如果PB＝AB，那么∠OAP就是直角.于是PA与⊙O相切；如果，那么PA与⊙O不相切.

图4

例2可以在等腰三角形的性质、矩形的判定的相关教学中使用.

三、构造三角形中位线

只用刻度尺可以画三角形中位线，基于这一点，可以设计一些构造三角形中位线画平行线的问题.

例3如图5，只用刻度尺，过点P画出直线AB的平行线.

图5

设计初思考：只用刻度尺，容易画出一个三角形的中位线，也就是画出了这个三角形一边的平行线，于是有了例3这个问题：只用刻度尺，能过一点画已知直线的平行线吗？这里涉及到了能否用三角形中位线建立模型.

画图方法：如图6，在直线AB上取点C，D，连接CP，量出CP的长.延长CP至点E，使得CP=PE，连接DE，量出DE的长，取DE的中点Q，画直线PQ.则直线PQ即为直线AB的平行线.

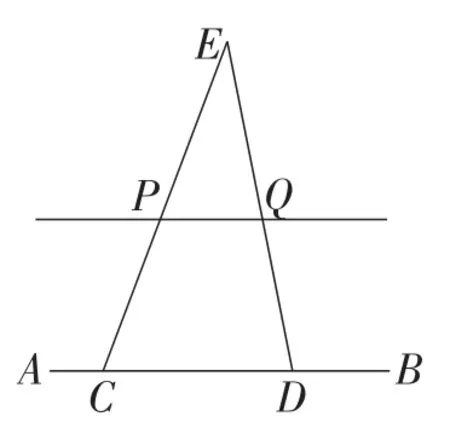
图6

三角形中位线蕴含了平行线，构造三角形中位线是画平行线的一种行之有效的方法.此例可以在三角形中位线的相关教学中使用.

四、构造平行四边形

从图形变换的角度看，平行四边形是揭示平移实质的重要图形.依据对角线互相平分的四边形是平行四边形，可以设计用刻度尺画平行线和等于已知角等问题.

例4如图7，已知点P在∠ABC的边BC上，请只用刻度尺，过点P画出∠DPC，使得∠DPC=∠ABC.

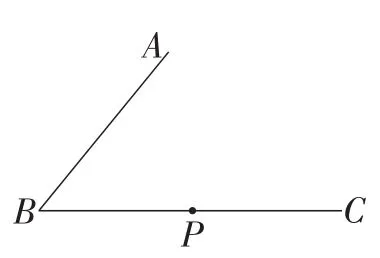
图7

设计初思考：只用刻度尺，能画平行四边形吗？当然，答案也是肯定的.有平行四边形，就有平行线，于是就有相等的角.就可以提出类似尺规作图中的基本问题：只用刻度尺画一个角等于已知角.

画图方法：如图8，在BA上取点E，连接PE，量出PE的长，取PE的中点O，连接BO，量出BO的长，延长BO至点D，使得OD＝BO，连接PD.则∠DPC即为所要画的角.

图8

通过四边形的对角线互相平分构造平行四边形，是画一条直线的平行线的又一种方法，无论点P在∠ABC的内部还是外部，均可以连接BP两次构造平行四边形，使BP成为所构造平行四边形的一条边来分别画出BA，BC的平行线，于是都可以画出等于∠ABC的一个角.

此例中，只用刻度尺画一个角等于已知角，实际上是化归为过点P画出BA的平行线，于是通过构造平行四边形解决这一问题.此例可以在平行四边形判定的相关教学中使用.

五、构造全等三角形

两个三角形全等，可得对应边、对应角分别相等，对一些与轴对称图形、中心对称图形相关的问题，设计只用刻度尺画图问题，有时还可以从构造全等三角形方面考虑.

例5如图9，∠BAC是轴对称图形，只用刻度尺，画出∠BAC的对称轴.

图9

设计初思考：用刻度尺画∠BAC的角平分线与画∠BAC的对称轴实际上等价的，能否有其他不同于例1的解决方法？显然，构造全等三角形解决问题是另一种选择.

画图方法：如图10，在∠BAC的边AB上分别取点D，E，量出AD，AE的长.然后在边AC上分别取点F，G，使得AF=AD，AG=AE.连接DG，EF，DG与EF交于点H.画出直线AH.则直线AH即为∠BAC的对称轴.

图10

此例中，构造的全等三角形有：△AEF≌△AGD，△HDE≌△HFG，△AEH≌△AGH.此例可以在三角形全等的判定的相关教学中使用.

例6如图11，只用刻度尺，判断直线AB与CD是否平行.

图11

设计初思考：此例实际上是例3的衍生，只用刻度尺，可以通过构造三角形中位线、平行四边形来画平行线.而只用刻度尺判断两条直线是否平行，不妨通过构造全等三角形来解决.

画图方法：如图12，在AB与CD上分别取点E和点F，连接EF，量出EF的长，然后取其中点O.画直线OH，交直线AB于点H.量出OH的长.在直线OH取点G，使得OG=OH.

图12

判断：根据三角形全等知识可得△OEH≌△OFG.可得∠OEH=∠OFG.于是GF∥AB.因此可得结论：如果点G是直线OH与CD的交点，那么AB与CD平行，否则AB与CD不平行.

除了构造全等三角形，此例也可以通过构造三角形中位线、平行四边形来解决，在相关内容的数学教学中均可以使用这一素材.

总之，设计只用刻度尺画图问题，其背后的操作依据都是图形建模，需要依据三角形、四边形等特殊图形的相关知识，实际上也是这些知识的延伸、拓展应用.在教学中设计系列化的单一工具画图，不仅能帮助学生巩固相应知识，而且能发展学生解决问题的策略，这无疑对提高数学教学的效能，培养学生的数学素养具有重要意义.