基于改进NSGA-Ⅱ算法的拖拉机传动系统匹配优化

傅生辉 李 臻 杜岳峰 毛恩荣 朱忠祥

(1.中国农业大学工学院， 北京 100083； 2.现代农业装备优化设计北京市重点实验室， 北京 100083)

0 引言

拖拉机动力传动系统的速比匹配直接决定整机作业性能，对其动力性和燃油经济性均有重要意义[1]。传统的拖拉机传动系统匹配设计多沿用汽车变速器设计方法，采用等比级数分配或依靠经验偏置等比级分配各挡传动比[2]，不能兼顾动力性和燃油经济性，充分发挥拖拉机工作性能，具有一定的局限性。

目前，针对拖拉机传动系统速比匹配研究较少，多集中在汽车领域，主要以最高车速、加速时间、驱动功率损失率、典型循环工况百公里油耗、能量利用率等为目标进行优化[3-7]。其中，张抗抗等[8]建立了以最高车速、加速性能和百公里电耗为目标函数的优化模型，通过多目标遗传算法对电动汽车传动比进行了优化设计；程方晓[9]提出一种基于自适应保持多样性遗传算法的传动系传动比优化方法，实现了不同类型车辆的传动系参数优化；雷嗣军[10]利用Matlab和Advisor实现了基于多目标遗传算法的汽车传动系统联合优化仿真设计；ZHANG等[11]根据爬坡能力和NEDC循环工况建立了汽车动力性和经济性优化模型，提出了基于模拟退火遗传算法的传动系匹配优化方法；王粉粉[12]综合考虑拖拉机不同挡位的实际作业需求，引入加权因子建立拖拉机动力性和经济性综合评价指标，利用遗传算法实现了拖拉机传动比的匹配优化。

多目标进化算法如今已成为求解复杂非线性NP问题的必要手段。常用的多目标进化算法主要有蚁群算法(Ant colony optimization，ACO)、强度帕累托进化算法(Strength pareto evolutionary algorithm，SPEA)、粒子群算法(Particle swarm optimization，PSO)、非支配排序遗传算法(Non-dominated sorting genetic algorithm，NSGA)等[13-17]。其中，DEB等[18]提出的NSGA-Ⅱ算法以其Pareto支配的选择模式并辅以密度估算选择胜出机制而成为多目标进化算法的典范，广泛应用于电网系统规划[19-24]、管网优化设计[25-26]、机械手轨迹规划等领域[27-28]，是迄今为止最优秀的多目标进化算法之一。但该算法通过计算聚集距离来保持种群分布性的机制存在一定缺陷，容易导致算法陷入局部最优[29]。

基于此，本文提出一种改进NSGA-Ⅱ算法，用于求解拖拉机动力传动系统速比匹配优化问题，通过优化传动系传动比分配，以期有效处理整机动力性和燃油经济性需求间的突出矛盾，提高拖拉机整机综合性能。

1 拖拉机传动系统匹配优化模型

1.1 目标函数的建立

以拖拉机驱动功率损失率和比燃油消耗损失率作为整机动力性和燃油经济性评价指标，建立传动系统优化匹配目标函数。

(1)驱动功率损失率

对于n挡变速箱，j挡下拖拉机驱动力为

(1)

式中Fqj——j挡下拖拉机驱动力，kN

Te——发动机转矩，N·m

ij——j挡的总传动比

ηc——总传动效率，%

rq——驱动轮动力半径，m

拖拉机各挡理论速度为

(2)

式中vj——j挡下的理论车速，km/h

ne——发动机转速，r/min

则j挡时驱动力曲线与横坐标所围面积为

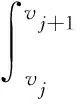
(3)

式中v——拖拉机理论车速，km/h

理想驱动特性曲线所围成面积为

(4)

式中Tp——最大功率时的输出转矩，N·m

np——最大功率时发动机转速，r/min

Fq——理想特性下的驱动力，N

驱动功率损失率ηFj定义为

(5)

驱动功率损失率反映了拖拉机传动系统特性与理想传动系统的差距，也反映了发动机动力性能的发挥程度，该值越小，说明发动机与传动系在动力性能方面匹配得越好。

(2)比燃油消耗损失率

拖拉机工况繁多，作业环境复杂，其燃油经济性无法仅用典型循环工况油耗或等速行驶百公里燃油消耗量等特定工况衡量。基于此，本文结合拖拉机牵引燃油消耗率和动力输出轴燃油消耗率定义，采用比燃油消耗损失率作为拖拉机燃油经济性评价指标，其值越小，说明拖拉机动力传动系统间的经济性匹配越有效。

(6)

式中ξgj——j挡时拖拉机比燃油消耗损失率

gTL——具有理想驱动特性的拖拉机比油耗

Agj——j挡时拖拉机比油耗曲线所围面积

Sgj——j挡时理想驱动特性下拖拉机比油耗曲线所围面积

gTj——j挡时的拖拉机比油耗

综上，拖拉机传动系统优化目标函数为

(7)

式中X——优化变量集合

f1(X)——动力性评价目标函数

f2(X)——经济性评价目标函数

1.2 传动比优化约束条件

拖拉机变速箱传动比分配需要满足设计理论车速、驱动力附着限制、最大牵引力、传动比公比等一系列约束条件。

(1)理论车速

若拖拉机Ⅰ挡在发动机额定转速ned下设计车速为Va，最低稳定转速nmin时设计起步车速为Vd，设计最高车速为Vc。而根据作业速度要求，基本作业挡中头挡理论车速vb应大于5 km/h，则拖拉机理论车速应满足

(8)

(9)

(10)

式中v1min——Ⅰ挡理论起步车速，km/h

v1——Ⅰ挡额定转速时理论车速，km/h

vmax——最高理论车速，km/h

ib、in——作业挡头挡和最高挡总传动比

(2)驱动力附着限制

受限于地面附着条件，最大驱动力应满足

(11)

式中Fqmax——最大驱动力，N

Qq——驱动轮垂直载荷，N

φ——允许附着系数，约为0.6～0.8

(3)最大牵引力

拖拉机最大牵引力按犁耕作业工况时基本作业的头挡计算，同时保留10%～20%的储备牵引力，以应对不同工况和农具引起的阻力变化。

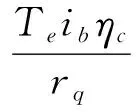
(12)

式中z——犁耕犁铧数，取5

b——单犁铧宽度，取30 cm

h——耕深，取25 cm

k——土壤比阻，取8 N·cm2

Ga——拖拉机质量，kg

f——滚动阻力系数，留茬地为例，取0.06

(4)滚动阻力

在公路运输工况下，拖拉机达到最高车速时，驱动力应克服滚动阻力，即

(13)

式中f′——公路滚动阻力系数，取0.03

Ted——拖拉机额定转矩，N·m

(5)相邻传动比公比

选取John Deere、Case IH、New Holland等品牌拖拉机装配的10款部分动力换挡变速箱，功率覆盖100～164 kW，对其变速箱传动比分配进行分析，如图1所示。

图1 动力换挡变速箱传动比公比Fig.1 Gear ratio of power-shift transmission

由图1可知，不同品牌的拖拉机变速箱虽然挡位数、功率范围等性能指标存在差异，但传动比公比均遵循以下原则：①动力换挡主变速箱传动比接近等比级分配，公比约为1.2～1.28。②区段换挡部分相邻挡位传动比公比在1.18～2.39之间，同一型号变速箱各区段均不相同，qAB>qCD>qDE>qBC。B、C区段为基本作业速度范围，挡位分布比较集中，传动比公比较小，而A区段多为缓行挡和爬行挡，D、E区段主要为运输挡，均不需要较多挡位，因此挡位分布相对稀疏，传动比公比较大。

2 改进NSGA-Ⅱ多目标优化算法

NSGA-Ⅱ算法核心思想如图2所示，针对其在非支配解的空间搜索能力和保持种群均匀性方面的不足，本文引入正态分布交叉算子(Normal distribution crossover，NDX)和差分变异算子来提高算法寻优能力。

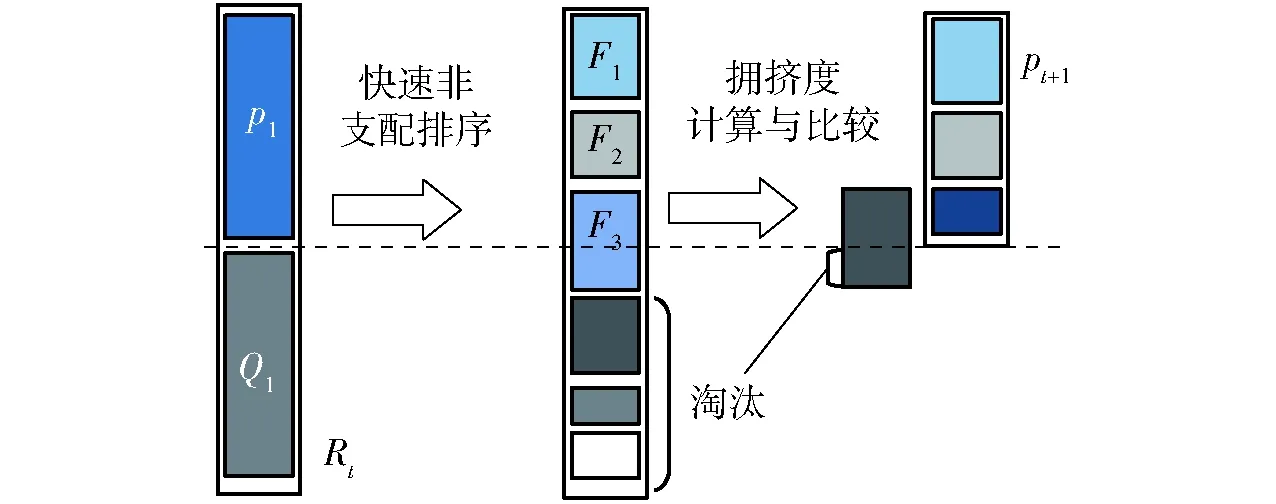
图2 NSGA-Ⅱ算法核心思想Fig.2 Core of NSGA-Ⅱ algorithm

2.1 正态分布交叉算子

利用NDX算子替代模拟二进制交叉算子(Simulated binary crossover，SBX)，在保证非支配解集质量基础上，进一步提升算法的全局搜索能力，更容易跳出局部最优。

假定父代p1、p2，NDX算子产生子代个体，对于第i个变量，其交叉过程为

(u≤0.5)

(14)

(u>0.5)

(15)

式中u——区间(0,1)的随机数

|N(0,1)|——正态分布随机变量

为验证NDX算子的合理性，本文在一维搜索空间对NDX算子和SBX算子搜索能力进行比较。给定两个父代个体空间位置，对两种算子独立计算6 000次，即分别产生12 000个子代个体，统计各自在搜索空间的分布情况，如图3所示，其中，p1=0.7，p2=0.2，搜索概率均为0.5。其搜索空间分布如图3所示，与SBX相比，NDX算子搜索范围更广，更容易跳出局部最优解，且更容易获得完整Pareto解。

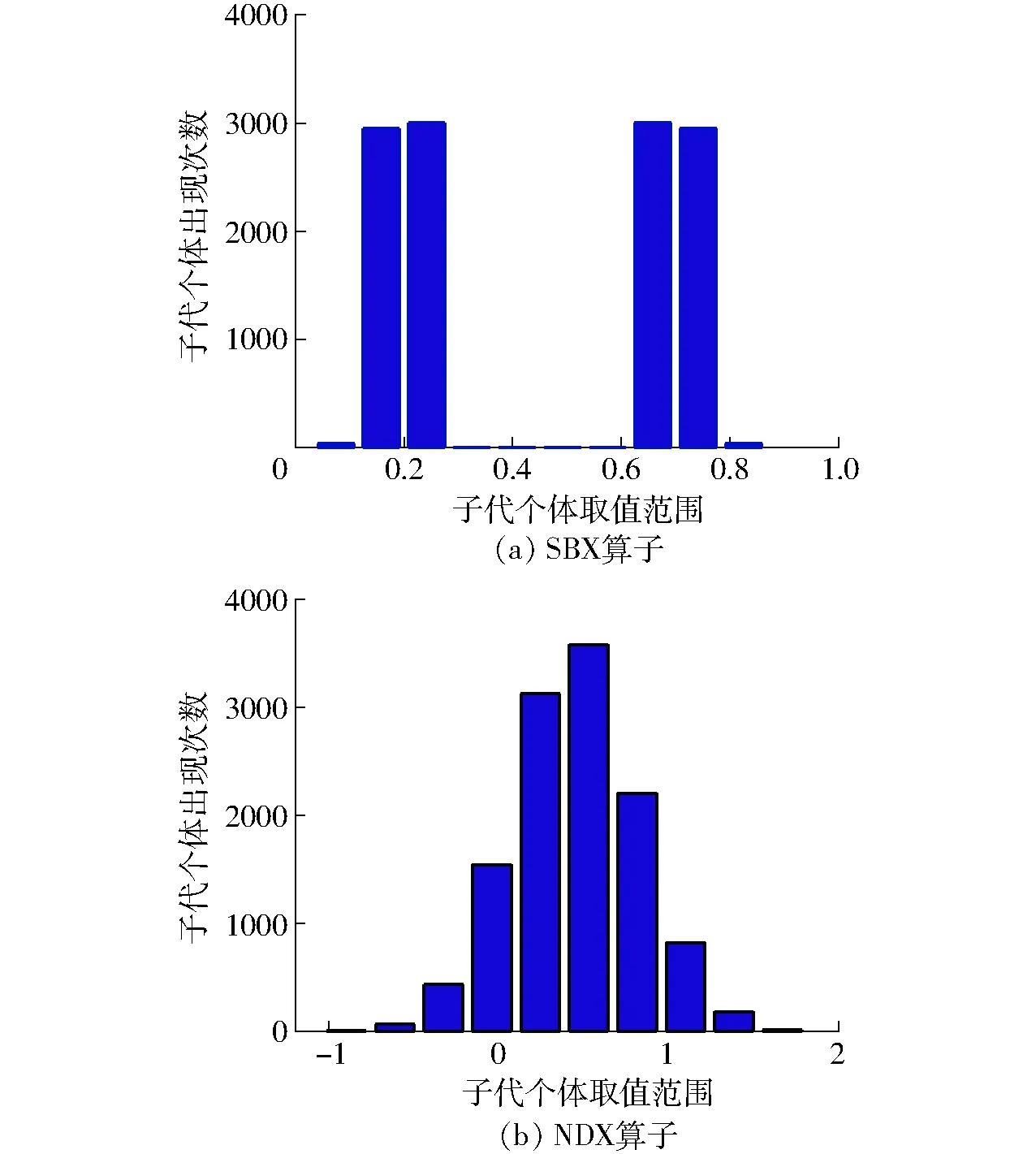
图3 两种算子一维搜索空间分布Fig.3 Search space distribution of NDX and SBX

2.2 差分局部搜索策略

差分算法(Differential evolution，DE)本质上是一种具有保优思想的贪婪遗传算法，采用差分变异策略对个体进化方向进行干预扰动，具有局部寻优的优势。因此，本文采用DE算法中的差分向量作为变异算子，提高算法的局部搜索能力。

(16)

式中r为相邻个体对变异方向的影响程度，区间为[0,1]。r值越大，影响程度越大。

差分局部搜索策略首先需要找到当前代种群中非支配层级最高的个体集F(1)，并通过计算距离阈值，选择需进行局部搜索的相邻个体，并利用式(16)产生新个体。其次，检查新个体与原始个体是否满足相互非支配关系，若满足，将新个体并入当前集合，形成新个体集，否则，丢弃新个体，然后计算新个体集的拥挤距离，根据拥挤距离保留新个体。其中，距离阈值和相邻个体选择具体如下：

(1)距离阈值。找到当前种群非支配集合F(1)在子目标i的两个极值端点，求解子目标i的目标值差，记为Di，根据

(17)

式中 |F(1)|——当代种群中最高层级的非支配集个体数目

计算子目标i的距离阈值δi。距离阈值δi在进化过程中将随|F(1)|的规模变化而动态调整，从而保证当代Pareto前沿的均匀分布。

(2)选择相邻个体。对非支配集按子目标i进行排序，将相邻个体的距离与子目标i的距离阈值δi进行比较。若大于或等于δi，且相邻个体在其他子目标下的目标值至少有一对不相等，则相邻个体需要执行差分局部搜索。差分搜索在进化初期有助于种群分布的均匀性和广泛性，避免算法陷入局部最优。

2.3 改进NSGA-Ⅱ算法流程

综上，改进NSGA-Ⅱ算法求解流程如图4所示。

图4 改进NSGA-Ⅱ算法流程图Fig.4 Flow chart of improved NSGA-Ⅱ algorithm

3 算法验证

为验证所提算法的有效性，采用4个不同的MOP测试函数ZDT1、ZDT2、ZDT3和ZDT6验证算法性能。此外，为评估Pareto解集的分布性，采用文献[29]提出的空间分布均匀性指标SP进行评价。SP值越小，解集分布越均匀。

(18)

其中di=min(|f1,j(x)-f1,i(x)|+|f2,j(x)-f2,i(x)|)

di——当前解集中第i个解的目标值与其最近邻解目标值的距离

程序运行环境为Matlab R2015a，算法设置参数为：初始种群50，进化代数500，交叉概率0.9，变异概率0.1。利用本文改进算法与原NSGA-Ⅱ算法求解测试函数的Pareto解集，并与测试函数真实的Pareto前沿(500个取样点)进行对比，结果见图5。

从图5可知，改进NSGA-Ⅱ算法与原NSGA-Ⅱ算法均得到了较好的Pareto前沿，但与原算法相比，本文算法收敛性相对较好，求得的Pareto解更接近测试函数的真实Pareto最优解，而且原NSGA-Ⅱ算法解集个体分布不均匀，在某些区域个体分布过于集中，而某些地方个体稀疏，甚至没有个体。运行10次统计得到SP均值及标准差。两种算法在不同测试函数上的分布性评价指标SP对比结果如表1所示，从表中可以看出，改进NSGA-Ⅱ算法在解集分布均匀性和稳定性方面均优于原NSGA-Ⅱ算法，进一步说明了本文算法的有效性。

4 传动比匹配优化分析

为验证本文算法的合理性和有效性，以表2所示的某型号拖拉机为例，利用本文算法对变速箱传动比进行优化。此外，与NSGA-Ⅱ算法、文献[12]中的加权遗传算法等进行对比试验。

图5 不同测试函数的Pareto前沿对比Fig.5 Comparison of Pareto fonts of test functions obtained by NSGA-Ⅱ and improved NSGA-Ⅱ

参照文献[30]，利用发动机台架试验数据建立发动机稳态输出转矩模型

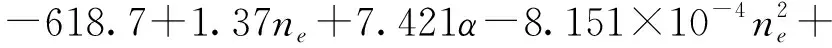
(19)

式中α——油门开度

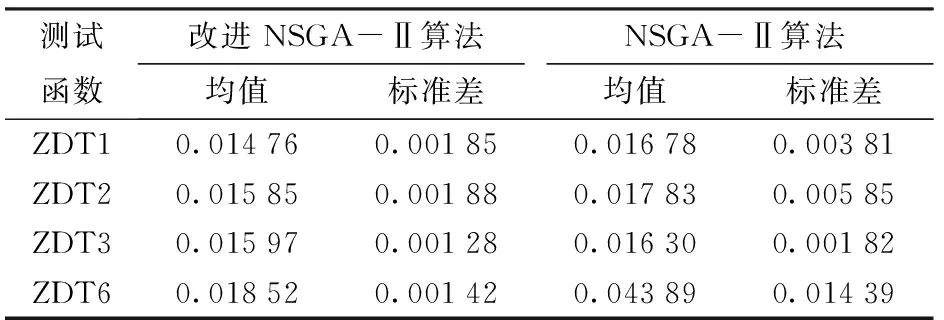
表1 算法的分布性SP均值及其标准差比较Tab.1 Comparison of average value and standard deviation of SP

表2 拖拉机整机及发动机基本参数Tab.2 Tractor and engine basic parameters

同理，建立拖拉机燃油消耗率模型

(20)

4.1 基于改进NSGA-Ⅱ算法的传动比优化

基于改进NSGA-Ⅱ算法的拖拉机传动比优化参数设置如下：初始种群为100，最大进化代数为200，交叉概率0.9，Pareto前端个体系数为0.3。根据非支配排序获取Pareto前沿，如图6所示，Pareto最优解分布较为均匀，连续性强，反映出本文算法具有良好的空间搜索与收敛能力。

图6 改进NSGA-Ⅱ算法优化结果Fig.6 Optimization results of improved NSGA-Ⅱ

为选出最佳传动比，引入隶属度函数，通过隶属度反映对目标优化结果的满意程度。综合拖拉机动力性和经济性目标函数的隶属度选取变速箱传动比最优配置。首先利用

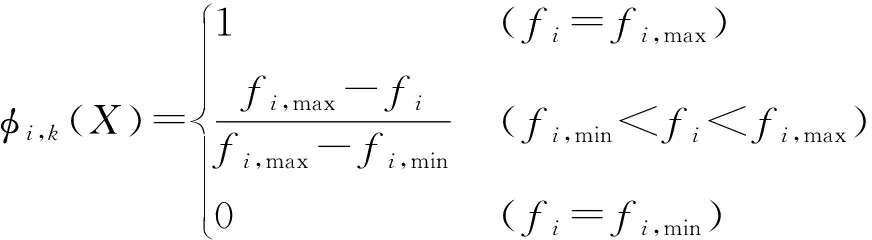
(21)

式中φi,k(X)——目标函数i第k个解的隶属度

fi,max、fi,min——目标函数最大值、最小值

计算Pareto解中所有目标函数的隶属度，然后根据拖拉机设计偏好设置权重，通过

(22)

式中λi——隶属度权重

φk(X)——第k个解的隶属度加权值

计算隶属度加权值，最大值对应的Pareto解为最优解。

4.2 优化结果对比分析

在算法对比试验中，NSGA-Ⅱ算法与本文算法的参数设置基本相同。加权遗传算法与文献[12]中的参数保持一致，交叉概率为0.8，最大进化代数为200，初始种群为100。利用3种不同算法实现的拖拉机传动比匹配优化结果如表3所示。

表3 基于3种算法的传动比优化结果对比Tab.3 Comparison of drive ratios optimized by three algorithms

从表3中可知，与优化前相比，3种算法优化后拖拉机传动比分配均有明显改变。Ⅰ～Ⅳ挡传动比降幅较大，基本作业挡与优化前基本保持一致，运输挡传动比优化结果差别明显。经本文算法优化后，除直接挡传动比保持不变外，其他运输挡传动比均略高于优化前传动比，排挡更稀疏，相应的速度变化范围更广。

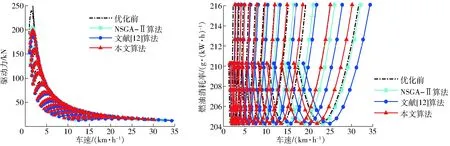
图8 3种算法优化的拖拉机动力性与经济性对比Fig.8 Comparison of tractor power and fuel economy optimized by three algorithms

为进一步分析各算法优化结果的差异，本文对比了采用不同算法得出的拖拉机理论车速，如图7所示。与优化前相比，优化后拖拉机各挡车速均有明显提高，速度分布更合理。其中，NSGA-Ⅱ算法与文献[12]算法优化结果基本一致，低速挡位车速明显提高，特别是Ⅰ挡理论车速分别提高17.82%和25.11%，其他挡位作业速度提高了1.28%～18.73%，最高车速分别达到了32.13、34.33 km/h。经本文算法优化后，Ⅰ挡车速提高了20.15%，最高挡车速降低至30.20 km/h，基本作业挡车速提高了0.48%～5.46%，Ⅳ挡车速达到4.99 km/h，基本作业挡覆盖范围更广。此外，除直接挡外，运输挡各挡工作速度分别降低了1.79%、3.70%和4.82%，变速箱排挡更集中，可满足不同的作业需求。

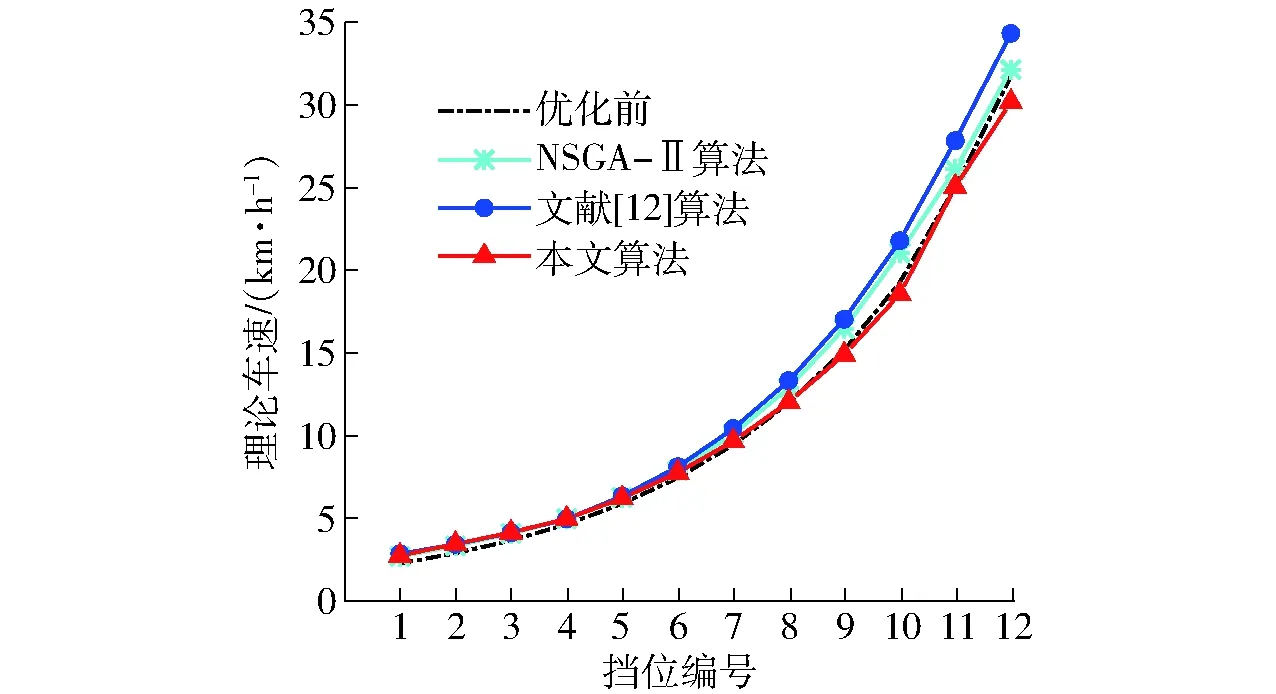
图7 基于3种算法优化的拖拉机理论车速对比Fig.7 Comparison of theoretical speeds optimized by three algorithms

图8为不同算法的拖拉机动力性与燃油经济性优化结果对比。由图8可知，优化后各挡驱动力略有下降，驱动功率利用率和燃油经济性显著提高。在5～20 km/h主要作业速度区间挡位分布较为集中。其中，文献[12]算法侧重拖拉机动力性表现，因此，整机的动力性优化效果最优，驱动功率损失率为20.19%，更接近理想驱动力曲线。然而比燃油消耗损失率为8.62%，低于NSGA-Ⅱ算法的6.29%和本文算法的4.23%。NSGA-Ⅱ算法和本文算法均能兼顾拖拉机动力性和经济性表现。采用本文算法后，拖拉机的驱动功率损失率和比燃油消耗损失率分别比NSGA-Ⅱ算法降低了4.17%和32.75%，比优化前降低了41.62%和62.80%，说明本文优化效果更佳。

表4为详细的优化前后拖拉机性能指标对比，从中可以看出，本文算法的优化效果更好，拖拉机车速范围更符合实际作业需求，速度分布更合理。此外，运输挡头挡爬坡度为45.07%，高于其他算法的39.57%和38.07%，较优化前提高了2.35%，整机性能得到明显改善。

表4 基于3种优化算法的拖拉机性能指标比较Tab.4 Performance comparison of tractor optimized by three algorithms

5 结论

(1)提出了一种改进NSGA-Ⅱ算法。该算法引入正态分布交叉算子和差分搜索策略，扩大了搜索范围，提高了算法的局部寻优能力，利用4组标准测试函数对改进算法进行了性能测试，证明了该算法的有效性。

(2)针对拖拉机传动比匹配优化问题，以拖拉机驱动功率损失率和比燃油消耗损失率作为动力性和燃油经济性评价指标，建立传动系统优化数学模型，基于改进NSGA-Ⅱ算法求解得到了Pareto解集，然后利用隶属度加权计算得到最优传动比分配。多种算法优化结果对比表明，本文方法可实现驱动功率损失率和比燃油消耗损失率分别降低41.62%、62.80%，运输挡头挡爬坡度提高2.35%，挡位分布更加合理，能够适应更多复杂工况。进一步验证了本文算法求解多目标优化问题的有效性。