丘陵地区刚性镇压轮性能仿真与试验
2018-12-04刘宏俊韩济远陈佳奇吕金庆赵淑红
刘宏俊 韩济远 陈佳奇 吕金庆 赵淑红
(东北农业大学工程学院, 哈尔滨 150030)
0 引言
在丘陵地区镇压作业时,由于地块小,坡度大,在保证播种机平稳性的前提下[1-2],对镇压要求较高。丘陵地区的土壤条件差异较大,如地势高的土壤含水率与地势低的土壤含水率差异明显;阳面坡地与阴面坡地的土壤含水率差异较大[3]。当土壤含水率变化时,需要控制载荷和加载时间(前进速度),达到较优的刚性镇压轮压实效果。载荷、前进速度和土壤含水率共同影响刚性镇压轮压实效果。由上述可知,在研究丘陵地区刚性镇压轮与土壤相互作用时,不能像平原地区采用准静态原则研究镇压与土壤相互作用机理[4-5],而应该加入速度变量,研究动态作用机理。本文对丘陵地区镇压对应的动态下陷量进行机理研究,完善适应于丘陵地区的镇压技术理论,逐步完善提升地区配套农业机械技术及装备,缩短与平原地区配套农业机械技术水平的差距[6-7]。
农业机械关键部件的研究多采用传统试验法(田间试验方法和土槽试验法)[8-10]。随着土壤本构模型及光滑粒子流体动力学(SPH)算法的日益完善[11-14],基于SPH算法的仿真试验法在农业机械中的触土部件与土壤的相互作用研究中越来越受到重视[15-18]。上述研究表明,SPH算法应用于刚性镇压轮与土壤的相互作用的研究具有可行性。
本文通过机理分析确定丘陵地区的动态土壤下陷量与土壤条件、工作参数的关系,并在此基础上建立刚性镇压轮与土壤相互作用的三维动态有限元模型,采用SPH算法研究刚性镇压轮与土壤的动态过程。以土壤含水率、载荷和前进速度为试验因素,选择下陷量和作业阻力为试验指标,旨在揭示丘陵地区刚性镇压轮-土壤的工作机理,以期为丘陵地区播种机及配套技术的研究提供理论及依据。
1 丘陵地区镇压作业机理分析
1.1 动态下陷量机理分析
镇压过程中土壤的力学性质和变形过程较为复杂,目前对某些参数(流动性、时间效应及应力应变等)的综合分析及相互作用关系的研究还不完善,而且丘陵山区条件下的相互作用研究鲜有报道。由于丘陵地区的特殊地形,镇压作业时土壤的物理性质、载荷、速度相互作用是个动态的过程,动态过程中刚性镇压轮下陷量的机理模型还未有人提出,而目前研究该过程多是在一定的假设条件下进行分析推算或由试验方法测得,往往是一种准静态预测。本文在基于准静态原则的镇压与土壤的机理模型中加入速度变量,建立动态镇压与土壤的机理模型。


图1 刚性镇压轮受力分析Fig.1 Force analysis of rigid press wheel

dQ=pBds
(1)
式中B——刚性镇压轮宽度
p——土壤抗压强度
刚性镇压轮受到的载荷与土壤的总抗压反作用力大小相等,则
(2)


(3)
由Bekker经验公式确定土壤抗压强度p与下陷量z0关系方程为
(4)
式中k——土壤变形模量n——土壤变形指数
土壤变形模量k与速度v2z的关系方程为[19]
(5)
式中k0——土壤变形静态模量
m——速度变化指数
由基点法及三角形相似定理得
(6)
联立式(3)~(6)可得
(7)
式(7)中有两个变量:x和z0。式(7)积分前,需将x替换z0。由图1的几何关系找出x与z0的关系式为
x2=r2-[r-(z1-z0)]2
(8)
简化式(8)可得
x2=2r(z1-z0)-(z1-z0)2
(9)
下陷量差值(z1-z0)相对刚性镇压轮直径2r较小,一般忽略不计[4],简化式(9)可得
x2=2r(z1-z0)
(10)
对式(10)进行变换得
(11)
将式(11)代入式(7)中,可得
(12)
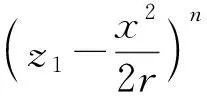
(13)
对式(13)进行积分可得
(14)
由式(11)可知,当z0=0时,x1与z1的关系式为
(15)
将式(15)代入式(14)得
(16)
由式(16)可知,刚性镇压轮的结构参数、土壤条件、前进速度和载荷共同影响土壤下陷量。实际镇压状态时,不同下陷情况下,刚性镇压轮与土壤的相互作用及运动趋势均不确定,而土壤作用模型可以获得之间的关系,前进速度越大,下陷越小,反之相反。载荷越大,则下陷量越大,反之相反。土壤相关参数对下陷量有影响,而具体的影响规律有必要通过试验进一步确定。
1.2 作业阻力机理分析
镇压作业时,由刚性镇压轮与土壤在接触处变形和摩擦而产生的力为作业阻力[20-21],其由3部分组成:刚性镇压轮压实土壤过程中前进阻力;推移土壤,形成波浪状凸起所需的推土阻力;土壤粘附在刚性镇压轮表面上所需的粘附阻力。由于形成土壤粘附的因素较多且复杂,无法用合适的数学公式表达,同时仿真模拟时无法模拟土壤粘附,在研究过程中重点分析前进阻力和推土阻力。由文献[22]和图1可确定前进阻力F1和推土阻力F2为
(17)
(18)
其中
Kc1=(Nc1-tanφ)cos2φ
式中Nc1、Nγ——太沙基承接能力系数
φ——土壤内摩擦角
c1——土壤内聚力
γ——土壤密度
刚性镇压轮镇压过程中的作业阻力F3为
F3=F1+F2
(19)
由式(16)、(17)可知,前进阻力F1与结构参数、土壤条件、前进速度和载荷有关;由式(18)可知,推土阻力F2主要与土壤条件和结构参数有关。故确定前进阻力F1和推土阻力F2的合力(作业阻力F)与结构参数、土壤条件、前进速度和载荷等均有关系,而具体的影响规律有必要通过试验进一步研究。
2 刚性镇压轮动力学模型建立
刚性镇压轮在丘陵山区的市场占有率很高,同时由于本文的丘陵地区镇压作业机理分析是基于刚性镇压轮建立的,为了保证研究的连贯性且具有代表性,本文选择刚性镇压轮作为研究对象。
2.1 土壤本构模型
针对东北丘陵地区黑壤土的特性,仿真采用LS-DYNA中的MAT147(MAT_FHWA_SOIL)土壤材料模型。该土壤材料模型采用修正的Mohr Coulomb屈服准则,其应力不变量等式表示为
(20)
式中P——静水压力
J2——应力偏张量的第二不变量
K(θ)——应力罗德角函数
α——修正后屈服面和标准Mohr-Coulomb屈服面之间贴近程度的参数
c——黏聚力
将土壤视为各向同性材料,及各部分的含水率、坚实度、密度等物理参数一致。为了解土壤条件对丘陵地区镇压轮的影响规律,选择3种典型东北地区土壤。东北丘陵地区黑壤土的主要参数如表1所示,其余参数采用软件默认值。

表1 土壤材料参数Tab.1 Parameters of soil
2.2 刚性镇压轮-土壤相互作用有限元模型
2.2.1刚性镇压轮有限元模型
为了控制仿真时间等问题,忽略影响仿真精度较弱的部位,简化刚性镇压轮物理模型为中空圆柱体(直径为300 mm,宽度为210 mm)。在LS-PrePost软件直接进行三维建模,并采用sweep方式对其进行网格划分,其网格单元类型为Solid164,如图2所示。刚性镇压轮材料参数:密度为7 800 kg/m3;弹性模量为2.1×1011Pa;泊松比为0.3。

图2 刚性镇压轮-土壤有限元模型Fig.2 Finite element model of wheel and soil
2.2.2土壤有限元模型
在LS-PrePost软件中直接按土壤模型长度为1 200 mm、宽度为400 mm、高度为400 mm的尺寸生成SPH土壤粒子,临近粒子之间的距离为10 mm,如图2所示。
2.3 边界条件
边界约束:约束模型中土壤底部的全部自由度;约束刚性镇压轮除绕轴转动以外的所有旋转自由度,同时仅约束刚性镇压轮横向移动自由度;整个模型加入重力,重力加速度为9.8 m/s2。接触算法为contact-automatic-nodes-to-surface。载荷加载:按照仿真要求,对镇压轮施加载荷及前进速度。LS-PrePost软件生成相应的K文件,然后递交给MPP LS-DYNA R8.1.0处理器求解,生成求解报告。
2.4 镇压作业过程分析
镇压轮在不同工况下,虽然指标数值不同,但是状态及规律相类似[23-24],故本文以前进速度为3 km/h、载荷为600 N、土壤含水率为12%仿真模型为例,重点分析刚性镇压轮与土壤相互作用的动态过程。
图3为不同时刻刚性镇压轮与土壤相互作用状态。由图3中的整个运动过程可知,不同深度处土壤竖向应力均有所增加,但不同土壤深度处,土壤竖向应力相差较大,且振幅的变化对表层土壤的竖向应力影响较大,而对深层土壤的竖向应力影响较小。
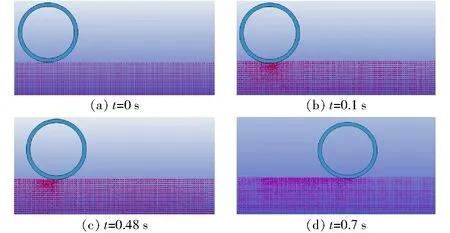
图3 刚性镇压轮镇压土壤动态过程Fig.3 Soil dynamic process of wheel
图4为下陷量的时间过程曲线。由图4可知,当载荷一定时,只要时间足够长,下陷量就能达到最大值,同时相比运动状态时,下陷量更大。由图3b到图3d过程中,刚性镇压轮的下陷量降低。由图3的定性分析和图4的定量分析确定前进速度影响下陷量。图4中包括3阶段:①a1阶段为静压阶段,土壤被向下和向两侧挤压,发生土壤变形,此阶段下陷量先陡增,后期平稳,这与平板试验的结果相符合,该阶段可证明仿真试验结果的可靠性。②b1阶段属于静压稳定状态,土壤阻力和载荷及重力几乎相等。③c1阶段为刚性镇压轮运动阶段,在c1阶段的初始阶段,由于前两阶段的下陷,造成轮子下方的土壤变硬。由b1阶段向c1阶段过渡时,在给定刚性镇压轮前进速度后,刚性镇压轮运动被向上抬起,故刚性镇压轮向上运动更大,进而土壤下陷量降低。在c1阶段的中后期,刚性镇压轮运动趋于相对平稳,但相比于b1阶段,下陷量围绕某一值上下波动,出现这种现象的主要原因是镇压作业时,土壤阻力发生变化,造成刚性镇压轮激振,这与实际情况相符合。在0.55~1.2 s,刚性镇压轮向前运动,轮子下方的土壤发生挤压变形,后方的土壤发生塑性变形,对距离土壤表面越远的土壤作用越轻。土壤向斜向下方挤压土壤,挤压的土壤发生变形,变形量较大。

图4 下陷量与仿真时间关系曲线Fig.4 Relationship curve between sinkage and simulation time
3 多目标优化试验
3.1 中心复合试验设计
借助数值模拟法研究试验因素(前进速度、载荷和土壤含水率)对试验指标(土壤下陷量和作业阻力)的影响规律。为了保证试验具有很好的序贯性、避免水平增加带来的复杂性和减少试验误差,采用中心复合表面试验设计(Central composite face-centered design,CCF)方法优化设计试验方案。基于CCF方案的编码值如表2所示,每组试验重复3次取平均值,在P=0.05 水平进行F检验。

表2 因素编码Tab.2 Experimental factors and codes
3.2 中心复合试验结果与分析
按照试验方案安排仿真试验,仿真试验结果如表3所示。其中x1、x2、x3分别表示载荷W、前进速度v和土壤含水率σ编码值。
3.2.1回归方程
采用Design-Expert 8.0.5b软件对试验数据进行分析,在置信度α=0.05下进行F检验,将不显著的因素和交互作用的偏平方和及自由度并入剩余平方和后,重新进行分析,保证所有因素都达到显著或极显著水平,得到优化的回归方程
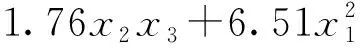
z=14.46+5.75x1+2.69x2+3.81x3-2.24x1x3+ (21)
3.2.2回归方程方差分析

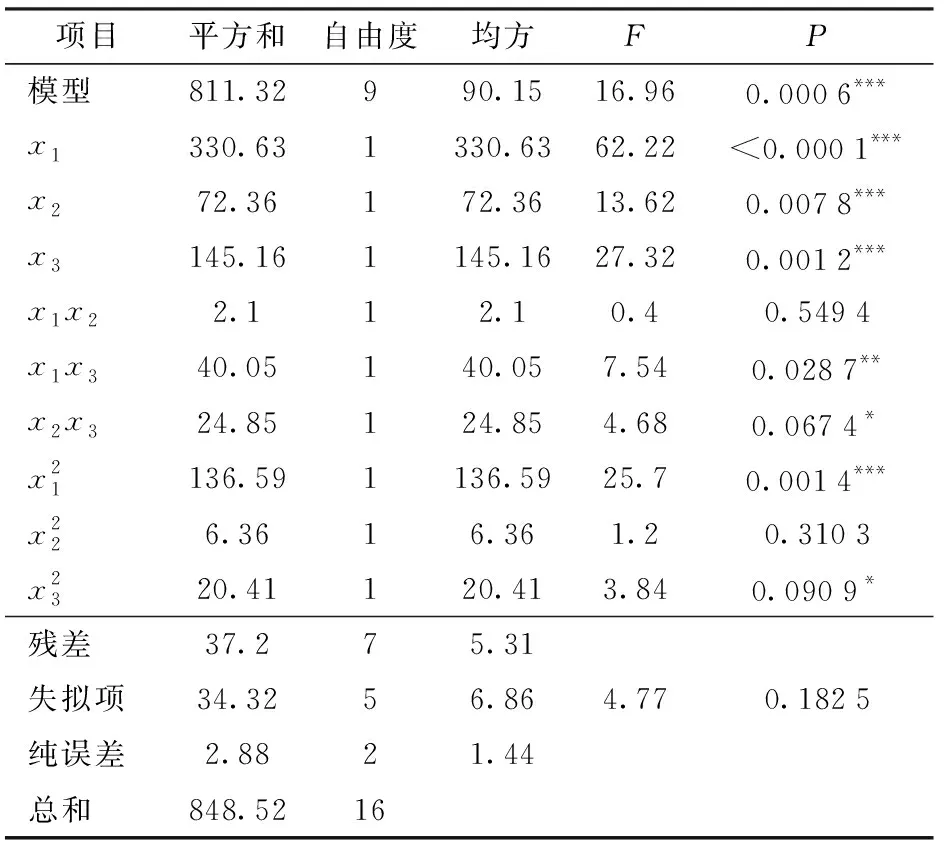
表4 土壤下陷量回归模型方差分析Tab.4 Variance analysis of regression equation for sinkage
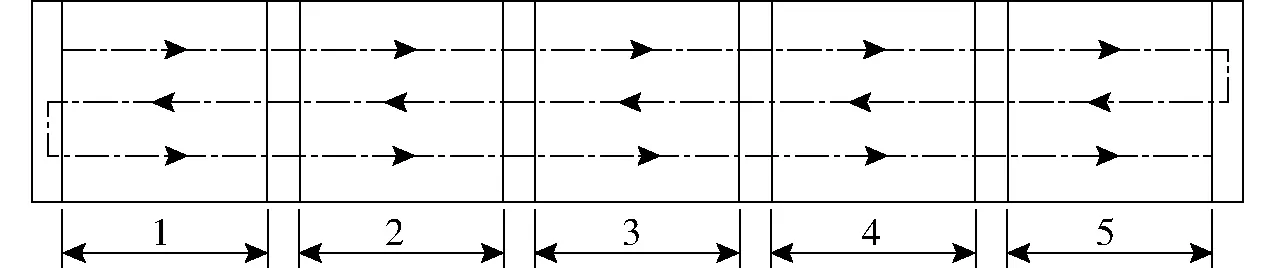
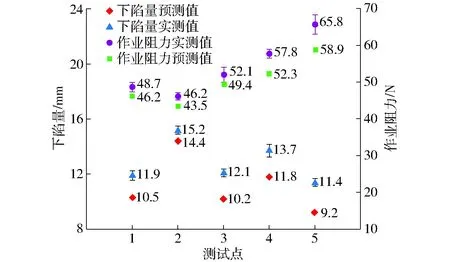
注:*表示较显著(0.05 表5 作业阻力回归模型方差分析Tab.5 Variance analysis of regression equation for working resistance 图5 因素之间的交互作用影响试验指标的响应曲面Fig.5 Response surfaces between interactions of factors and experimental indicators 3.2.3各因素对试验指标影响规律 因素交互与试验指标之间的关系规律如图5所示。由图5a可知,在载荷一定时,前进速度与下陷量的关系趋于线性,同时随着前进速度的增加,下陷量增加;在前进速度一定时,下陷量随着载荷的增加,先降低后增加。当载荷较大和前进速度较大时,下陷量较大。当载荷较小和前进速度较小时,下陷量较小。由图5b可知,在载荷一定时,土壤含水率与下陷量的关系趋于线性;在土壤含水率一定时,载荷与下陷量的关系也趋于线性。下陷量均随着因素增加而增加。由图5c可知,在载荷一定时,当前进速度较小时,前进速度增加,作业阻力增加不明显,而当前进速度超过某一前进速度后,作业阻力增加迅速;在前进速度一定时,载荷对作业阻力影响较明显,随着载荷递增,工作阻力增加。由图5d可知,在载荷一定时,当土壤含水率较大或较小,作业阻力较小,而当土壤含水率处于中间水平附近,作业阻力较大。在一定土壤条件下,以一定的载荷压实土壤时,由于土壤中含水率由少增多,土壤下陷量逐渐增加。当土壤中含水率达到某一值时,下陷量最大。 蚁群算法已经成功应用于若干领域,其中最成功的应用是组合优化问题[25-26]。作为一种全局搜索算法,蚁群算法能够有效地避免局部极优,但对于大空间的多点全局搜索,却不可避免地增加搜索时间。为了使算法能够更好更快的找到问题获得最优解,在其搜索过程中加入针对具体问题的局部搜索算法。 基于R语言的蚁群算法对多目标进行优化。采用加权距离法将两个目标方程合并成一个全局方程,具体转换方程y1为 (23) 式中t1x、t2x——第1、2项指标最大值与最小值的差值 t1d、t2d——第1、2项指标的平均值 μ1、μ2——第1、2项指标权重 下陷量直接影响出苗率与幼苗生长情况,并且最终影响作物产量;作业阻力直接影响功耗,即作业成本。由此可知,在镇压作业过程中,下陷量是主要考虑指标,而作业阻力是次要考虑指标。根据各指标的重要性及专家经验法,确定下陷量、作业阻力的权重μ1、μ2分别为0.75、0.25。 目标函数 对目标函数进行蚁群算法多目标优化后,获得目标函数之间的权衡曲线,一组非支配解(Pareto最优解)如图6所示。 图6 蚂蚁算法优化后的最优解前沿分布Fig.6 Distribution of Pareto front from ant colony algorithm 丘陵地区实际作业时,土壤含水率随着地形及地势改变而改变,属于不可控因素。当土壤含水率改变时,若不改变相应的载荷和前进速度,镇压效果较差。同时土壤含水率的实际变化是一个连续变化的过程,若不是智能镇压系统,则无法实时改变载荷和前进速度,来保证镇压效果。由文献[27]可知,丘陵地区的土壤含水率一般在12%~20%波动。本文将土壤含水率范围分成5份,由优化结果得到每个土壤含水率对应的载荷和前进速度,进而保证丘陵地区镇压作业时镇压效果一直处于较优水平。由该原则从Pareto最优解集中筛选出土壤含水率为(12±0.1)%、(14±0.1)%、(16±0.1)%、(18±0.1)%、(20±0.1)%的5组最优解,并将求解时的水平与实际值进行编码转换,得到最优水平组合,如表6所示。 表6 最优水平合集Tab.6 Optimal level set 验证试验在黑龙江省农业机械工程科学研究院的室内土槽中进行,如图7所示。试验设备:双向仿形镇压装置[19];刚性镇压轮;TCC-3型土槽试验车;土槽;六分力测试装置;SC-900型土壤坚实度仪。试验条件:土壤为典型东北黑土;土壤容重为1 311 kg/m3;土壤内摩擦角为18.1°。 图7 土槽试验Fig.7 Soil bin tests1.双向仿形镇压装置 2.刚性镇压轮 试验前,按照含水率由小到大依次排列对土槽分段,共5段,每段长度为5 m,如图7b所示。在土槽内每段土壤含水率均达到对应表6中土壤含水率后,镇压轮按照图8的箭头方向进行运动。同时按照表6中土壤含水率对应的工作参数进行试验,每组验证试验重复4次。试验验证结果与仿真优化结果如图9所示。 图8 试验方案分布及实施图Fig.8 Distribution and implementation diagram of test plans 图9 试验验证图Fig.9 Chart of verification test result 由图9可知,仿真结果与实测结果相差较小,出现这种现象可能是土槽中的土壤情况更复杂,数值模拟无法完全模拟出来,但是模拟结果的误差均小于12%,由此表明试验优化结果的可靠性,同时也验证了仿真的可行性。 (1)针对丘陵地区镇压作业特点,在传统刚性镇压轮与土壤作用模型的基础上加入前进速度变量,建立刚性镇压轮作业时刚性镇压轮与土壤的动态相互作用模型,为研究丘陵地区镇压动态过程中 土壤阻力和变形过程提供理论支撑。 (2)采用SPH算法建立刚性镇压轮与土壤相互作用的三维动态有限元模型,重点分析刚性镇压轮与土壤的相互作用,预测不同的作业参数对刚性镇压轮作业效果的影响。 (3)选择土壤含水率、载荷、前进速度为试验因素,选择下陷量和作业阻力为试验指标,采用中心复合表面试验方案获得回归模型,然后采用蚁群算法对回归模型进行多目标优化,获得不同含水率下的最优水平组合,然后进行土槽试验对最优水平组合加以验证,对比结果表明试验结果合理。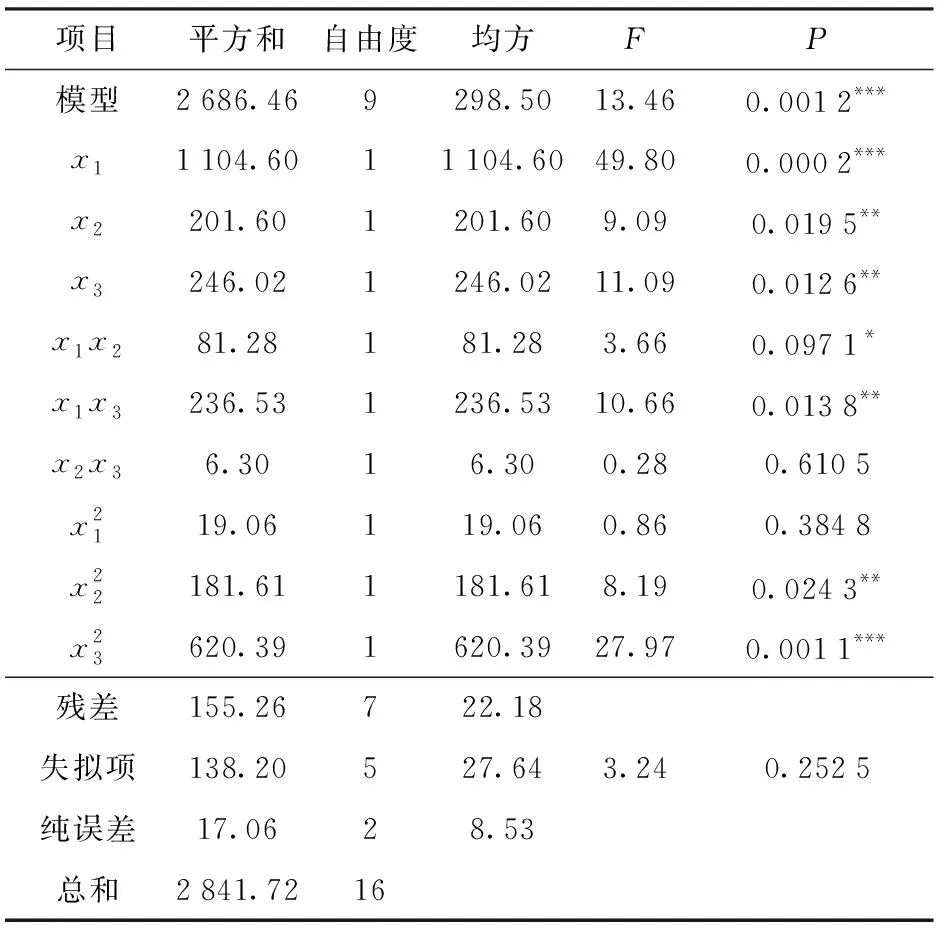

3.3 基于R语言蚁群算法的多目标优化
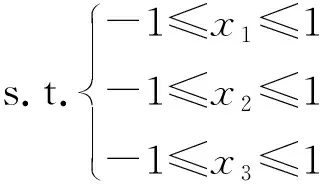


3.4 试验验证

4 结论
