控制回路性能评估在火电厂中的应用

林振锋，张 伟

(上海理工大学 光电信息与计算机工程学院，上海200093)

火电发电厂热工系统中存在大量的控制回路，控制系统决定着发电过程的安全性和经济性，因此对控制系统性能进行评价在火电发电厂中占据重要位置[1]。控制系统性能评估是通过实际过程数据，并对这些数据进行分析得出一个评价指标从而得出当前控制回路的性能和运行状态[1]。性能评估不会对回路产生额外的影响，并且能够较准确地衡量回路的健康状况。

1989年Harris提出了基于最小方差控制为基准的性能指标[3]，为控制回路性能评估奠定了基础。2002年Grimble提出带有惩罚项的广义最小方差法，该方法引入了误差权和控制权，使控制回路更加平稳，控制作用更加温和[4]。由于实际工业系统多数都是非线性的，传统的性能评估方法难以获得合理的评估效果，2007年Harris等将最小方差基准推广到一类非线性单变量系统中[5]。Sendjaja, Kariwala and Fu给出了控制器为 PID 系统的性能评估方法，能够直观有效的评估PID控制系统的性能好坏[6-8]。带遗忘因子的最小方差算法是基于过程数据，采用时间序列分析方法建立简单的扰动模型，与其他评估方法相比，它的评估结果更加准确，对工业过程中的时变模型适应性更强[9]。本文通过对海门电厂的低加水位控制系统进行性能评估，从结果中可以看出带遗忘因子的最小方差算法对时变模型适应性更强、精度更高。

1 最小方差性能指标

Harris最先提出了最小方差控制评估方法。该方法是一种只用日常闭环操作数据来评估控制回路性能的有效方法,且不会对系统的正常运行产生干扰，因此在实际工业控制系统中获得了广泛应用[10]。该方法的控制目标是最小化过程的输出方差，最小方差控制被用来作为评估当前控制回路的性能基准。Harris的性能指标定义为

(1)

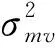
2 带遗忘因子的最小方差算法

带遗忘因子的最小方差算法是基于过程数据的最小方差性能评估方法，过程的输入输出数据不需要任何预处理。该算法的核心是采用时间序列分析方法建立扰动模型。在一定条件下，输出可看作是以白噪声为输入，经过扰动模型和过程模型的线性定常随机系统的响应。考虑单输入单输出反馈控制系统，如图1所示。

图1 单输入单输出反馈控制系统方框图

其中，Q为控制器传递函数，T为无时滞的过程传递函数，N为扰动传递函数，ε(t)为白噪声，τ是系统的延时。由图1可知，系统的输出为

(2)

N用丢番图表示为

N=f0+f1q-1+…+fd-1q-d+1+Rq-d
F=f0+f1q-1+…+fd-1q-d+1

由时间序列分析技术辨识系统的扰动模型可以得到系统的输出为

y(t)=F(q-1)ε(t)+L(q-1)ε(t-τ)

(3)

其中

(4)

设F(q-1)ε(t)=e(t)，可以得到

(5)

取前m项可得

7) 对开裂的填充墙的处理：由于填充墙的裂缝可能会损坏相关配电设备，因此对裂缝表面涂抹环氧树脂，并在墙体外侧进行防水处理，可用防水卷材.

(6)

利用系统闭环输出数据，可以通过时间序列分析拟合如下模型矩阵

y=Xθ+e(t)

(7)

式中，各向量形式如下

参数θ可以由最小二乘法得到

θ=(XTX)-1XTy

(8)

所以理论上的最小方差为

(9)

实际系统的输出方差为

(10)

(11)

3 评估步骤及参数选取

带遗忘因子最小方差算法的性能评估具体步骤如下：

(1)根据扩展时域法估计延迟时间τ。延迟时间τ能够直接影响性能指标，通常情况下很难直接获得回路的延迟时间，那么可以采用扩展时域法[12]。Desborough与Harris和Thornhill等提出扩展时域性能指标[12]，该指标定义为

(12)

其中b是预测时域。若b等于系统延迟时间τ，ηb就等于Harris指标η。但当ηb是在b大于延迟时间计算的，就叫做扩展时域指标。分别取不同的预测时域b，对所求得的扩展时域指标进行分析比较，可以确定系统延迟时间τ；

(2)采样时间和模型阶次的选择。采样时间选择应和控制时间一致。模型阶数m，它既是滑动平均项中的参数，又是回归参数θ的维数。m越大误差就越小，考虑到当m=5时，一般误差就可以被忽略，但是m太大就会使矩阵θ维数过高从而计算量变大，所以一般取5≤m≤30，本文m取30；

(3)遗忘因子β的选取。遗忘因子β的选取是该算法的关键，其严重影响系统性能评估的精度。β太小会使模型利用的采集数据长度过小，β太大则造成时变效果强的控制回路衰减效果不明显，这两种情况均会对系统性能评估结果产生影响。根据文献[9]中分析了β的选取范围，为了保证采集数据有足够长地有效长度以及满足评估结果的时变有效性，通常β的取值在[0.990，0.997]之间；

带遗忘因子最小方差算法的评估步骤流程，如图2所示。

图2 带遗忘因子最小方差算法性能评估步骤流程图

4 在低加水位控制系统中的应用

4.1 数据采集

以广东海门电厂的6号低加水位控制系统为研究对象，收集了约10 000个系统的输出和设定值数据(采样时间为1 s)，系统过程数据如图3所示。

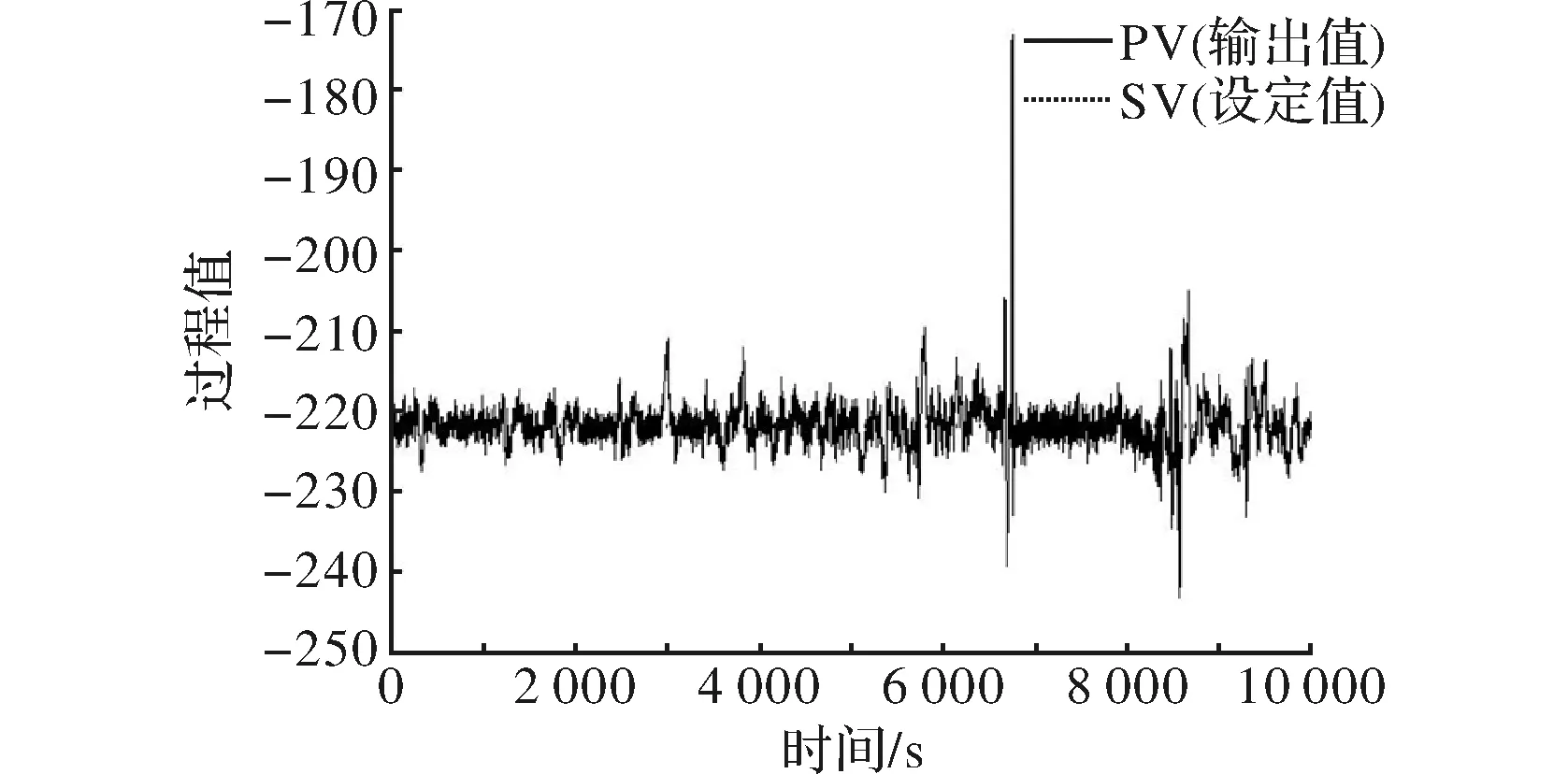
图3 低加水位控制系统过程数据

4.2 参数选取

(1)将现场采集到的10 000个数据分成10组，每组1 000个数据，即N=1 000。并根据第3节中步骤(2)的分析取模型阶数m=30；

(2)把现场采集的数据结合上文提到的扩展时域法，将预测时域b分别取不同值，求得对应的扩展时域指标，通过对比分析扩展时域指标对可以估计系统延迟时间τ为15 s；

(3)在第3节中步骤(3)提到影响β的选取因素有采样数据长度和时变效果。因此本文选取了不同β值进行实验，根据结果分析β为0.996时适合本文所选的系统过程数据。

4.3 评估结果

将上文选取的参数分别带入带遗忘因子的最小方差算法和不带遗忘因子的最小方差算法中，得到的性能指标如表1所示，绘制曲线图如图4所示。由图4可知，在同一个控制回路现场采集的连续10组数据评估结果表明：不带遗忘因子的最小方差算法的评估性能指标波动较大，波动范围在[0.544，0.940]之间，得到的性能指标无法正确有效表征实际控制回路的性能好坏；而采用带遗忘因子的最小方差算法的评估性能指标波动范围较小在[0.655，0.950]之间，说明控制回路性能较好，不需要进行设备维护和参数整定。

图4 低加水位控制系统评估结果曲线图

组别12345678910η(不带β)0.8030.7080.5440.6210.8400.5920.9400.8650.5720.546η(带β)0.8630.6910.7360.7210.8930.6550.9600.8610.7240.691

5 结束语

本文以火力发电厂的低加水位控制系统为研究背景，分别将带遗忘因子和不带遗忘因子的最小方差算法应用到性能评估过程中。从评估结果中可以看出，带遗忘因子的最小方差算法比传统的不带遗忘因子最小方差算法更具有时变有效性，评估结果范围更加稳定，可以更有效的表征控制系统的性能好坏。此外，带遗忘因子最小方差算法是利用过程输出数据通过时间序列分析方法进行建模，不仅对回路的运行不会产生干扰还简化了处理大量数据的过程。因此，带遗忘因子的最小方差算法更适用于低加水位控制系统的性能评估。