无线网络中分布式机会协作的信道接入算法研究
2018-12-03乐婷婷
陈 倩,骆 骏,乐婷婷
(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)
在分布式无线网络中,随着传输数据量的增大及传输速度的加快,现有的频谱资源已无法满足发展的需求[1]。为了有效解决频谱资源紧缺的问题,需要合理高效的利用无线信道对数据进行传输,避免拥塞及频谱资源的浪费[2-3]。因此,实现分布式无线网络高效最优的信道接入是十分必要的。
在文献[4]中,Dong L等人提出了一种基于DF中继的信道接入算法(Decoding Forwarding-Channel Access,DF-CA)。该算法考虑了一个分布式DF中继网络,源节点首先对探测报文进行发送,在获得第一跳信道信噪比(Signal to Noise Ratio,SNR)之后,源节点对放弃,直接链接发送或继续探测第二跳以进行决定。如果源决定探测第二跳,则估计第二跳的信道SNR,并继续决定放弃或发送,最后实现信道接入。该算法虽然在一定程度上实现了有效的信道接入,却严重浪费了第一跳的频谱资源,且当第二跳信噪比较大时,算法性能会大幅下降。
为了实现更快速准确的信道接入,本文提出了一种基于竞争的具有解码转发中继的分布式机会信道接入算法(Distributed Opportunity Channel Access,DOCA),该算法分别提出了第二跳和第一跳的最优信道接入策略,即采用请求发送(Request To Send,RTS)和清除发送(Clear To Send,CTS)的握手方式进行信道争用。如果源节点获胜,则估计第一跳信道中的信道状态信息,并且确定胜者源是放弃还是继续。若放弃,则让所有源开始新的争用;若继续,则由中继进行第二跳信道的一系列探测。最后,对比DF-CA算法和NCA(Naive Channel Access)算法。仿真结果表明,当第二跳信道具有较大的平均信噪比时,DOCA算法在吞吐量和数据包延迟方面都有性能提升。
1 系统模型
1.1 定义
假设一个分布式解码转发中继网络场景,该场景具有M个源-目的节点对,且每个源-目的节点对具有一个DF中继。现考虑从源到目的节点有直接链接的情况,第一跳信道的探测如下:源节点对探测分组进行发送,如果信道中没有发生冲突,则探测分组由中继和目的节点接收[5]。通过接收的探测分组,中继可以估计从源到中继节点的信道信噪比,然后将其信道SNR信息报告给目的节点,由目的节点做出第一跳的决定。对于直接链接情况,中继可以通过接收报告消息来实际估计从源节点到其自身的信道SNR。目的节点将具有两跳的完整信道SNR信息:即从源节点到中继,从中继到目的节点,从源节点到目的节点。最后,通过获取的SNR信息,目的节点对源和本身之间的端到端传输速率R进行计算,根据实际的传输速率R来决定最优的信道接入方式。因此,虽然从源到目的节点的通信具有两跳,但是可以视为具有可达速率R的虚拟一跳通信。
1.2 系统建模
在本文中,将主要考虑源-目的节点之间无直接链接的情况,其系统建模如下:假设i个源-目的节点对,从源节点i到中继(第一跳)和从中继到目的节点 (第二跳)都遵循瑞利衰落,其平均接收SNR分别表示为ηi和ρi[6-7]。首先,M个源节点进行信道争用,过程如下:在具有持续时间σ的小时隙中,每个源节点向中继发送具有概率p的RTS,如果没有源节点发送,则小时隙处于空闲状态,概率为(1-p)M,所有源在下一个小时隙中开始新的信道争用。如果有多个源节点发送RTS,概率为1-(1-p)M-Mp(1-p)M-1,则将发生信道冲突,所有源节点在碰撞超时后开始新的信道争用[8-9]。如果只有一个源节点发送RTS,概率为Mp(1-p)M-1,即称该源节点为获胜源。
现将观测值定义为从信道争用的起始点到获胜源出现的间隔[10],若RTS被中继节点成功接收,则观测值的平均持续时间表示为
(1)
其中,τRTS和τtimeout分别表示为RTS和超时的持续时间。
在观测结束后,获胜源的中继节点通过接收的RTS估计获胜源到自身的信道SNR,并确定放弃或停止。其中放弃表示为:放弃传送机会,并通过发回CTS通知获胜源,CTS也将受到其它源节点的接收,随后所有源节点开始新的争用。停止表示为:停止当前进程并利用第一跳传输机会发回CTS通知源节点[11-12]。然后,获胜源以传输速率Rn在通道相干时间的持续时间τd内进行传输。
现假设观测值为n,如果获胜源停止,则将回报Yn表示为获胜源发送并由目的节点接收的总交通流量,Tn表示观测值从1~n的时间与两跳中用于传输的持续时间和。若N表示为停止时间,则意味第N-1次观测的获胜源不会停止,而第N次观测的获胜源停止,定义N*为最佳的停止时间,使系统实现最大的系统吞吐量,即
N*=argsupN≥0E[YN]/E[TN]
(2)
其中E表示期望,N*表示最佳停止策略,将式(2)转化为使λ>0的YN-λTN最大化问题。对于λ>0,应找到表示为N*(λ)的最优策略,可以最大化预期回报
U(λ)=supN(λ)≥0{E[YN(λ)]-λE[TN(λ)]}
(3)

2 第二跳最优信道接入策略
在本节中,将首先考虑最优的第二跳信道接入策略,假设观测值为n,则获胜源表示为w(n),停止或传输给中继的速率表示为Rn。对于第二跳,中继需要向目的节点发送RTS,目的节点接收到RTS后,对第二跳信道信噪比rg进行估计,且返回一个包括信道SNR信息的CTS[13-14]。如果给定可实现的第二跳传输速率log2(1+rg)≥Rn,则中继节点需要在持续时间τd内以传输速率Rn向目的节点发送;如果log2(1+rg) 为了有效解决第二跳中一系列的决策问题,将提出新的算法如下:Sl表示第二跳的信道接入策略,中继节点对第二跳的l个通道进行检测,如果中继在l个通道的检测中找不到大于等于Rn的可实现的第二跳传输速率,则中继节点选择放弃。将Vl(λ)表示Sl的净回报,第二跳策略的最优化可以转换为达到净回报的最大值{E[V1(λ)],E[V2(λ)],…,E[V∞(λ)]},则可以得到 (4) (5) 其中,Fw(n)(·)表示为胜者源w(n)对应中继的第二跳信道SNR的累积分布函数。 根据式(4)和式(5),得到 E[V∞(λ)]-E[Vl(λ)]=(Fw(n)(rn))l (6) 从式(6)中可以得到 E[Vl+1(λ)]-E[Vl(λ)]=(Fw(n)(rn))l(1-Fw(n)(rn)) (7) 如果式(7)满足E[V∞(λ)]≥λτd,则E[V1(λ)]≤E[V2(λ)]≤…≤E[V∞(λ)],最优的第二跳策略可以表示为:中继继续探测第二跳信道,直到可达到的速率不小于Rn为止。如果式(7)满足E[V∞(λ)]<λτd,则E[V1(λ)]>E[V2(λ)]>…>E[V∞(λ)],最优的第二跳策略可以表示为:中继只探测第二跳信道一次,如果可实现的传输速率不小于Rn,则发送,否则放弃。 基于上文中导出的最优第二跳信道接入策略,进而得出了最优第一跳信道接入策略。第一跳中,在观测值n处,由中继节点接收获胜源w(n)的RTS,并估计第一跳信道SNR的rf(n),以较高的回报为准来决定是放弃或停止。如果第一跳的决定是放弃,则净回报表示为-λτCTS;如果第一跳的决定是传输,则净回报表示为最大的{E[V1(λ)],E[V2(λ)],…,E[V∞(λ)]}-λ(τCTS+τd),其中τCTS+τd表示第一跳中的时间成本:中继使用CTS通知源的决定,源在持续时间τd进行发送。 对于第二跳信道接入,现在考虑E[V∞(λ)]<λτd的情况,可以得到{E[V1(λ)],E[V2(λ)],…,E[V∞(λ)]}=E[V1(λ)]则第一跳传输的净回报表示为:E[V1(λ)]-λ(τCTS+τd)。由于E[V∞(λ)]<λτd,在式(6)中,当l=1可以得到 E[V1(λ)]=(1-Fw(n)(rn)) (8) 因此,式(8)将导致E[V1(λ)]-λ(τCTS+τd)<-λτCTS,即第一跳传输的净回报小于第一跳中放弃的净回报,即胜者源将永远放弃第一跳。在计算第一跳的传输净回报时,可以忽略E[V∞(λ)]<λτd的情况,而只需关注E[V∞(λ)]≥λτd的情况,第一跳传输停止的净回报表示为如下 (9) (10) 在解决第二跳策略时,满足U(λ*)=0的λ*的问题(3)的最优停止策略是问题(2)的最优停止策略。所以,应该关注λ*的问题(3)的最优停止策略,问题(3)的最大预期回报U(λ*)应满足最优性方程 (11) 其中1/M表示源为获胜源的概率,Ew(n)[·]表示rf(n)遵循均值信噪比为ηw(n)的瑞利衰落时的期望[15-16],而λ*通过设置U(λ*)=0从最优方程数值进行计算所得。因此,第一跳中胜者源w(n)的最优停止策略表示为 (12) 对于每个胜者源w(n),不等式(12)的左侧表示为rf(n)的非递减函数,将rf,w(n)表示为使不等式(12)中两边相等的rf(n)的解。然后,第一跳中的最优停止策略被重写为N*(λ*)=min{n≥1:rf(n)≥rf,w(n)}。 为了验证所提算法的有效性及准确性,将对DOCA算法,DF-CA算法和NCA算法在吞吐量和数据包延迟方面进行仿真比较。其中,吞吐量表示单位时间内信道成功传送数据的数量,吞吐量越大,表示信道接入算法准确度越高;数据包延迟表示在数据包发送过程中,因冲突等因素所造成的时间延迟,数据包延迟越小,表示信道接入算法有效性越高。因此,对参数设置如下:假设模拟网络中有18个采样对,且系统带宽设为2 MHz,σ=20 μs,τRTS=103 μs,τCTS=τtimeout=106 μs,τd=8 ms,ρ=0.1,ηi=1,ρi=ρ∀i,第二个平均信噪比ρ从1变化到20。 图1 第二跳平均信噪比与吞吐量的仿真示意图 为了间接证明DOCA算法具有较高的准确性,将对DF-CA算法、NCA算法和DOCA算法在吞吐量方面进行比较。如图1所示,显示了DF-CA算法、NCA算法和DOCA算法吞吐量随第二跳平均信噪比变化的示意图。从图中可以看出,随着第二跳平均信噪比的增加,3种算法的吞吐量也逐渐升高,但DOCA算法和DF-CA算法的吞吐量高于NCA算法。当ρ低于5时,DF-CA算法的吞吐量高于DOCA算法,如当ρ= 2时,DF-CA算法的吞吐量比DOCA算法高28%。当ρ>5时,DOCA算法的吞吐量高于DF-CA算法,如当ρ= 20时,DOCA算法的吞吐量比DF-CA算法高出14%。综上,对比DF-CA算法和NCA算法,DOCA算法的准确性较优。 图2 第二跳平均信噪比与平均数据包延迟的仿真示意图 为了间接证明DOCA算法具有较高的有效性,将对DF-CA算法、NCA算法和DOCA算法在数据包延迟方面进行比较。如图2所示,显示了DOCA算法,DF-CA算法和NCA算法的数据包延迟随第二跳平均信噪比变化的示意图。从图中可以看出,当ρ= 1时,交通流量负载大于系统容量,因此3种算法的数据包延迟较大。当ρ增加时,系统容量增加,数据包延迟降低。对于ρ≥2,DOCA算法和DF-CA算法的数据包延迟相似,且均小于NCA算法的10%。这是因为,在DOCA算法和DF-CA算法中,通过放弃传输机会或让中继等待,每个传输具有更高的速率,因此系统中的排队延迟降低。 总体而言,将第一跳平均信噪比标准化为1,则系统吞吐量与第二跳平均信噪比ρ的曲线可以在DOCA算法和DF-CA算法中进行离线数值绘制,两条曲线的交点给出了一个阈值ρ+。当ρ>ρ+时,采取DOCA算法,当ρ≤ρ+时,采取DF-CA算法。这样,当信噪比从低到高时,均可以实现良好的性能。 在分布式无线网络中,随着高速数据传输的需要与发展,通过一个快速准确的信道接入方式来合理利用现有频谱资源是目前的研究热点。为此,本文提出了一种基于竞争的具有解码转发中继的分布式机会信道接入算法(DOCA),该算法分别提出了第二跳和第一跳的最优信道接入策略,即采用请求发送RTS和清除发送CTS的握手方式进行信道争用,如果源节点获胜,则估计第一跳信道中的信道状态信息,并且确定胜者源是放弃还是继续;若放弃,则让所有源开始新的争用;若继续,则由中继进行第二跳信道的一系列探测。最后,对比DF-CA算法和NCA算法,仿真结果表明,当第二跳信道具有较大的平均信噪比时,DOCA算法在吞吐量和数据包延迟方面都有性能提升。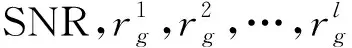
(E[V∞(λ)]-λτd)
(E[V∞(λ)]-λτd)3 第一跳最优信道接入策略
E[V∞(λ)]+Fw(n)(rn)λτd<λτd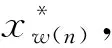
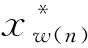
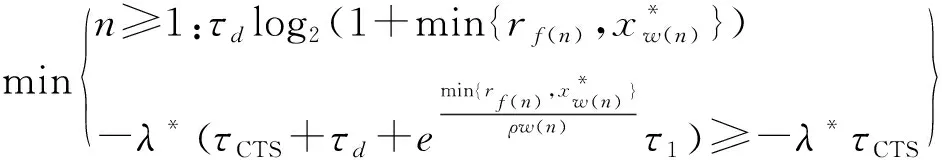
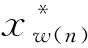

4 仿真分析


5 结束语
